Nesta página você verá o que é a matriz Identidade (ou Unidade) além de vários exemplos. Além disso, explicamos quais são as propriedades da matriz identidade, como trabalhar com esse tipo de matriz e qual o resultado do seu determinante. Por fim, você encontrará as aplicações que esta matriz tão particular possui.
Qual é a matriz identidade?
A matriz Identidade (ou Unidade) é uma matriz quadrada preenchida com zeros (0), exceto na diagonal principal, onde todos os elementos são uns (1).
Esta é a definição de matriz identidade ou matriz unitária, mas certamente você verá isso mais claramente através de exemplos:
Exemplos de matrizes de identidade
Exemplo de matriz identidade de dimensão 2 × 2
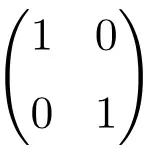
Exemplo de matriz de identidade de ordem 3×3

Exemplo de matriz de identidade de tamanho 4×4
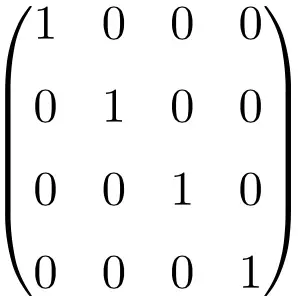
Como você pode ver, para construir a matriz identidade ainda precisamos seguir o mesmo procedimento: colocar uns (1) na diagonal principal e o restante todos zeros (0). A única coisa que muda é o tamanho da mesa.
Propriedades da tabela de identidade
A matriz identidade, a matriz unitária ou mesmo a matriz idêntica é muito utilizada em matemática, e isso se deve às características que esse tipo de matriz possui:
- A matriz identidade é um exemplo de matriz diagonal .
- Uma matriz unitária é uma matriz triangular superior e inferior.
- A matriz identidade também é uma matriz simétrica .
- O deputado da matriz identitária é ele mesmo.
![Rendered by QuickLaTeX.com \displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16454b80729e9e2059e118dfc5ba2f8a_l3.png)
- É uma matriz invertível. E, quanto ao adjunto, o inverso da matriz Unidade é ele próprio:
![Rendered by QuickLaTeX.com \displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e9ca14cfbc1b230347abb6e36464e9c_l3.png)
- Qualquer matriz escalar pode ser obtida a partir da multiplicação de um número pela matriz identidade:
![Rendered by QuickLaTeX.com \displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ba48a8806ab085937939bada831e91e_l3.png)
- Todos os autovalores (ou autovalores) da matriz Idêntica são 1:
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b9a461140ed125bbcc26d551b255cdc_l3.png)
- Por fim, a matriz identidade também é um exemplo de matriz de permutação .
Operações com a matriz Identidade (ou Unidade)
Você provavelmente está pensando: tudo isso é muito bom mas… e para que serve a matriz de Identidade? Se ao menos fosse uma tabela com 0s e 1s!
Embora você ainda não tenha dado esse tópico, a matriz identidade é muito usada em matemática, na verdade, esse tipo de matriz quadrada é muito importante na álgebra linear. A principal utilidade da matriz identidade é a facilidade com que permite cálculos de operações matriciais. Então vamos ver como trabalhar com a matriz Identidade:
Adicionando e Subtraindo com a Matriz de Identidade
Uma maneira de adicionar (ou subtrair) números na diagonal principal de uma matriz sem alterar os outros elementos é usar a matriz identidade, porque ela adiciona (ou subtrai) apenas uma unidade a esses números. elementos:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a357b8c79a1f4f70a5dcdeadcbe3e46_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f549edd3cac0340615dae86bf7e2932_l3.png)
Você também pode adicionar ou subtrair mais unidades aos elementos da diagonal multiplicando primeiro a matriz identidade por um escalar:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-85520cb04e8697d315a6e5002c8e1dea_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a90c8c3b8f9635561f6c85e7b003734c_l3.png)
Multiplicação de uma matriz pela matriz identidade
Ao multiplicar uma matriz pela matriz identidade, ela atua como um elemento neutro , ou seja, qualquer matriz multiplicada pela matriz identidade resulta na mesma matriz. Dê uma olhada no seguinte exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-345f47fb447c1877462d8c9358f8eb89_l3.png)
Além disso, o significado do produto da matriz é irrelevante, ou por outras palavras, não importa se multiplicamos a matriz identidade pela direita ou pela esquerda porque o resultado será sempre a mesma matriz. Para demonstrar isso, repetimos o exercício anterior, mas desta vez multiplicando a matriz Identidade pelo lado oposto:
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9a6c50074dc2594054453a6b53f4862_l3.png)
Poder da matriz identidade
A potência da matriz identidade sempre resulta na matriz identidade, independentemente do expoente ao qual elevamos a matriz e da dimensão da matriz.
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e8dbc082f20a9a9b5b5c9b1b443833c4_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67a36555e36ab97ce2c663bf32c8e97d_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2efa9dcf6ec3b986aaff19701a794899_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14cad3370ec38fd0ed7ebb3a5fa96282_l3.png)
Determinante da matriz identidade
Como presumo que você já imagine, o determinante da matriz Identidade (ou Unidade) é sempre igual a 1 , independente da dimensão da matriz.
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-718871901f1660f8f5202ea312c39584_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5971cf3c43e11184380d55d43f69ba8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4efd00fdafcbe456d1b5060344fe8d5_l3.png)
Aplicativos de matriz de identidade
Por fim, depois de todas essas informações, você provavelmente já sabe responder à típica pergunta de por que a matriz identidade é tão importante? Relaxe, eu também já me fiz essa pergunta. 😂
Como você deve ter notado, a matriz identidade tem muitas utilidades e por isso é tão interessante. Uma das utilizações da matriz unitária são as operações, pois, como vimos, é muito fácil realizar operações matriciais com ela.
Por outro lado, a matriz identidade também é usada para resolver equações matriciais . Para fazer isso, usamos a seguinte propriedade da matriz inversa: multiplicar uma matriz por sua matriz inversa é igual à matriz identidade. Você pode ver como resolver uma equação com matrizes clicando no link.
Além disso, a matriz identidade também é usada para calcular a matriz inversa com o método gaussiano. Este método envolve colocar uma matriz próxima à matriz identidade, formando assim uma matriz maior. Então, a matriz original deve ser transformada em uma matriz identidade aplicando operações elementares nas linhas. Parece muito complicado mas na realidade não é tanto, porém todo um procedimento deve ser aplicado, então se você tiver mais interesse pode pesquisar como inverter uma matriz no mecanismo de busca da página web (de cima para a DIREITA).
Por fim, a matriz Identidade também é útil para diagonalizar uma matriz e calcular seus autovalores (ou autovalores). Porque por meio de certas operações, nas quais intervém a matriz unitária, pode-se obter o polinômio característico do qual são obtidos os autovalores. Mas já é um assunto bastante avançado, por isso temos uma página inteira super abrangente dedicada à diagonalização de matrizes com exemplos e exercícios resolvidos explicando-o. Se você estiver mais interessado, pode procurar este guia em nosso mecanismo de busca (canto superior direito).