Nesta página veremos como discutir e resolver um sistema de equações com parâmetros . Além disso, você encontrará exemplos e exercícios resolvidos de sistemas de equações lineares para praticar.
Por outro lado, para analisar sistemas de equações lineares é importante que você saiba o que é a regra de Cramer e o que é o teorema de Rouché–Frobenius , pois os utilizaremos constantemente.
Exemplo de sistema de equações lineares com parâmetros
- Discuta e resolva o seguinte sistema de equações em termos do parâmetro m :
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ab2286d15c20029b98a5ea4622033d4_l3.png)
Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
Agora resolvemos o determinante de A usando a regra de Sarrus, para ver qual é a classificação da matriz:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e823f83f25f798bd854612a7352680d4_l3.png)
Portanto, o resultado do determinante de A depende do valor de m . Veremos, portanto, para quais valores de m o determinante desaparece. Para fazer isso, definimos o resultado igual a 0 :
![]()
E resolvemos a equação quadrática com a fórmula:
![]()
![Rendered by QuickLaTeX.com \displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e863082ac1f9b43df4de9fe93f5eb305_l3.png)
Então quando m for igual a 2 ou 3, o determinante de A será 0. E quando m for diferente de 2 e diferente de 3, o determinante de A será diferente de 0.
Devemos, portanto, analisar cada caso separadamente:
m≠3 e m≠2:
Como acabamos de ver, quando o parâmetro m é diferente de 2 e 3, o determinante da matriz A é diferente de 0. Portanto, o posto de A é 3 .
![]()
Além disso, o posto da matriz A’ também é 3 , porque dentro dela existe uma submatriz 3×3 cujo determinante é diferente de 0. E não pode ser de posto 4 pois ‘não podemos fazer um determinante 4×4.
![]()
Então, como o posto da matriz A é igual ao posto da matriz A’ e ao número de incógnitas do sistema (3), pelo teorema de Rouché-Frobenius sabemos que se trata de um Sistema Determinado Compatível (SCD) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Uma vez que sabemos que o sistema é um Sistema Determinado Compatível (DCS), aplicamos a regra de Cramer para resolvê-lo. Para fazer isso, lembre-se que a matriz A, seu determinante e a matriz A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac47361358555f733a42cffecabdbe9_l3.png)
Para calcular x com a regra de Cramer, trocamos a primeira coluna do determinante da matriz A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b17f49436fdadbb014011b5c461a4a56_l3.png)
Para calcular y com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a2bf75bdabfb2c83870f1869ce19e3d_l3.png)
Para calcular z com a regra de Cramer, trocamos a terceira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eebb3c4d280afc8a9aed8877ddcd4ac5_l3.png)
Portanto, a solução do sistema de equações para o caso m≠3 e m≠2 é:
![]()
Como você pode ver, neste caso a solução do sistema de equações é função de m.
Uma vez encontrada a solução para quando m é diferente de 2 e 3, resolveremos o sistema para quando m é igual a 2:
m=2:
Analisaremos agora o sistema quando o parâmetro m for igual a 2. Neste caso as matrizes A e A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f42ec4801f3e84cd44b4e0b2ae6351cf_l3.png)
Como vimos anteriormente, quando m=2 o determinante de A é 0. Portanto, a matriz A não é de posto 3. Mas dentro dela possui 2×2 determinantes diferentes de 0, por exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
Então, neste caso , a classificação de A é 2 :
![]()
Uma vez conhecida a classificação da matriz A, calculamos a classificação de A’. O determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis na matriz A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c68c742cae37c52ad2566b7feec5301_l3.png)
Todos os determinantes possíveis de dimensão 3×3 dão 0. Mas, obviamente, a matriz A’ tem o mesmo determinante 2×2 diferente de 0 que a matriz A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
Portanto, a matriz A’ também é de posto 2 :
![]()
Assim, como o posto da matriz A é igual ao posto da matriz A’ mas estes dois são menores que o número de incógnitas do sistema (3), sabemos pelo teorema de Rouché-Frobenius que este é um sistema indeterminadamente compatível (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Por se tratar de um ICS, precisamos transformar o sistema para resolvê-lo. Para isso, devemos primeiro eliminar uma equação do sistema, neste caso iremos deletar a última equação:
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10c7facda35cb8894e6bbb236e4953f1_l3.png)
Agora vamos converter a variável z em λ:
![Rendered by QuickLaTeX.com \begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0155083595420da31a486927e953805c_l3.png)
E colocamos os termos com λ com os termos independentes:
![Rendered by QuickLaTeX.com \begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8486baee4be39f417988ee12b5e67c7_l3.png)
Portanto, a matriz A e a matriz A’ do sistema permanecem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8591e8c21bce2f49998311bbb08f7dee_l3.png)
Finalmente, uma vez transformado o sistema, aplicamos a regra de Cramer . Para fazer isso, primeiro resolvemos o determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3](https://mathority.org/wp-content/ql-cache/quicklatex.com-c34669d7234c9736c350f793df337bd3_l3.png)
Para calcular x com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-987ebe052154332042afeb27535996f1_l3.png)
Para calcular y com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a3c7b2cd7319f7f9db6df7df79abb50_l3.png)
De modo que quando m=2 a solução do sistema de equações é função de λ, pois é um SCI e portanto possui infinitas soluções:
![]()
Já analisamos a solução do sistema quando o parâmetro m é diferente de 2 e 3, e quando é igual a 2. Portanto, precisamos apenas do último caso: quando m assume o valor de 3:
m=3:
Analisaremos agora o que acontece quando o parâmetro m é 3. Neste caso as matrizes A e A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49bbc0d7d36606aa59be050c2682de5_l3.png)
Como vimos anteriormente, quando m=3 o determinante de A é 0. Portanto a matriz A não é de posto 3. Mas dentro dela possui 2×2 determinantes diferentes de 0, por exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d88ce42feb4bba9aa74aae98e1062c4a_l3.png)
Então, neste caso , a classificação de A é 2 :
![]()
Uma vez conhecida a classificação da matriz A, calculamos a classificação de A’. O determinante das 3 primeiras colunas dá 0, portanto tentamos outro determinante 3×3 que está dentro da matriz A’, por exemplo o das 3 últimas colunas:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e6f1a5c155ca004c73e51bdcbe5ece9_l3.png)
Por outro lado, a matriz A’ contém um determinante cujo resultado é diferente de 0, portanto a matriz A’ é de posto 3 :
![]()
Assim, quando m = 3, o posto da matriz A é inferior ao posto da matriz A’. Assim, do teorema de Rouché-Frobenius, deduzimos que o sistema é um Sistema Incompatível (SI) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3454f804b63f3cca9bcf08bc93815f90_l3.png)
Portanto, o sistema de equações não tem solução quando m = 3.
Resumo do exemplo:
Como vimos, a solução do sistema de equações depende do valor do parâmetro m . Aqui está o resumo de todos os casos possíveis:
- m≠3 e m≠2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf366a55bd307517f94fd8aa00cdf598_l3.png)
- m=2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94002d4f4d866569ed7d6993dd977b81_l3.png)
- m=3:
![]()
O sistema não tem solução.
Aqui fizemos todo o processo usando o teorema de Rouche e a regra de Cramer, mas sistemas de equações com parâmetros também podem ser discutidos e resolvidos pelo método de Gauss (com exercícios) . Você pode aprender mais sobre este método na página do link, onde encontrará uma explicação detalhada do procedimento, bem como exemplos e exercícios resolvidos passo a passo.
Problemas de discussão resolvidos de sistemas de equações lineares com parâmetros
Exercício 1
Discuta e resolva o seguinte sistema de equações lineares dependentes de parâmetros:
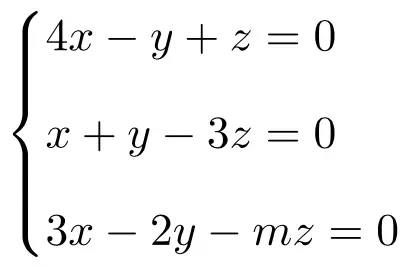
Primeiro fazemos a matriz A e a matriz estendida A’ do sistema:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b641845325965882d4aac899246cffb3_l3.png)
Devemos agora encontrar o posto da matriz A. Para isso, verificamos se o determinante de toda a matriz é diferente de 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d36c7cffe0248a2f45cd5871abc6ed5_l3.png)
O resultado do determinante de A depende do valor de m. Veremos, portanto, para quais valores de m o determinante desaparece. Para fazer isso, igualamos o resultado resultante a 0 e resolvemos a equação:
![]()
![]()
![]()
Assim, quando m for -4, o determinante de A será 0. E quando m for diferente de -4, o determinante de A será diferente de 0. Devemos, portanto, analisar cada caso separadamente:
m≠-4:
Como acabamos de ver, quando o parâmetro m é diferente de -4, o determinante da matriz A é diferente de 0. Portanto, o posto de A é 3.
![]()
Além disso, o posto da matriz A’ também é 3, porque dentro dela existe uma submatriz 3×3 cujo determinante é diferente de 0. E não pode ser de posto 4 pois ‘não podemos fazer um determinante 4×4.
![]()
Portanto, aplicando o teorema de Rouché-Frobenius, sabemos que este é um sistema determinado compatível (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Uma vez sabendo que o sistema é um SCD, aplicamos a regra de Cramer para resolvê-lo. Para fazer isso, lembre-se que a matriz A, seu determinante e a matriz A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9e0bd352ad7713a03824ead1239041c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20](https://mathority.org/wp-content/ql-cache/quicklatex.com-530cb4576ee1a91d6246ed6cf9dd0fc8_l3.png)
Para calcular xatex] com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna de termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b076bbda8d086abedb459570d74c80a9_l3.png)
Para calcular a incógnita e com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna de termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f642a8cb2fd174e5c383a4df53e11a2e_l3.png)
Para calcular z com a regra de Cramer, trocamos a terceira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5020a9ba4995b9715d8d1fb4720952b1_l3.png)
Portanto, a solução do sistema de equações para o caso m≠-4 é:
x=0 y=0 z=0
m=-4:
Analisaremos agora o sistema quando o parâmetro m for -4. Neste caso as matrizes A e A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e585e6465d27ea27ccc2c1a6ec1fe9ae_l3.png)
Como vimos anteriormente, quando m=-4 o determinante de A é 0. Portanto, a matriz A não é de posto 3. Mas dentro dela possui 2×2 determinantes diferentes de 0, por exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
Como a matriz possui um determinante de ordem 2 diferente de 0, a matriz A é de posto 2:
![]()
Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então tentamos os outros determinantes 3×3 possíveis:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-39fc49c7a63920c8956703a4851ecfc0_l3.png)
Todos os determinantes 3×3 da matriz A’ são 0, então a matriz A’ também não terá classificação 3. Porém, dentro dele possui determinantes de ordem 2 diferentes de 0. Por exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
Portanto, a matriz A’ será de posto 2:
![]()
A extensão da matriz A é igual à extensão da matriz A’ mas estas duas são menores que o número de incógnitas no sistema (3), portanto, de acordo com o teorema de Rouché-Frobenius, c é um Sistema Compatível Indeterminado (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f43fdf4978386c61d18f9bb5b5883881_l3.png)
É um sistema ICS, então precisamos transformar o sistema para resolvê-lo. Primeiro eliminamos uma equação, que neste caso será a última:
![Rendered by QuickLaTeX.com \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d5499fda37d3cbf56fbf6ecbfc6bfba_l3.png)
Agora vamos converter a variável z em λ:
![Rendered by QuickLaTeX.com \begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96ea68274b072531365282e01d926718_l3.png)
E colocamos os termos com λ com os termos independentes:
![Rendered by QuickLaTeX.com \begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6192715e62cc8e3d3fe4c51da8629c70_l3.png)
Tal que a matriz A e a matriz A’ do sistema permanecem:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-99a91208ff1742f81e799aa5ab7f9097_l3.png)
Finalmente, uma vez transformado o sistema, aplicamos a regra de Cramer. Para fazer isso, primeiro resolvemos o determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5](https://mathority.org/wp-content/ql-cache/quicklatex.com-34832b783ddaf4af205302240d0feafb_l3.png)
Para calcular x com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-362167d2eaa02d7243dedd5c385d08b1_l3.png)
Para calcular a incógnita e com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna de termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ede5a3a87ac0bb9ceea4232ec7b381fd_l3.png)
De modo que quando m=-4 a solução do sistema de equações é função de λ, pois é um SCI e portanto possui infinitas soluções:
![]()
Exercício 2
Discuta e encontre a solução para o seguinte sistema de equações lineares dependentes de parâmetros:
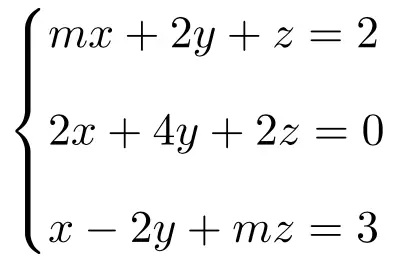
A primeira coisa a fazer é a matriz A e a matriz estendida A’ do sistema:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
Devemos agora encontrar o posto da matriz A. Para isso, verificamos se o determinante de toda a matriz é diferente de 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d0f8dbb7408ac6521e0144ac2f3a8a3_l3.png)
O resultado do determinante de A depende do valor de m. Veremos, portanto, para quais valores de m o determinante desaparece. Para fazer isso, igualamos o resultado resultante a 0 e resolvemos a equação:
![]()
![]()
![]()
![]()
![]()
Assim, quando m for +1 ou -1, o determinante de A será 0. E quando m for diferente de +1 e -1, o determinante de A será diferente de 0. Devemos, portanto, analisar cada caso por:
m≠+1 e m≠-1:
Como acabamos de ver, quando o parâmetro m é diferente de +1 e -1, o determinante da matriz A é diferente de 0. Portanto, o posto de A é 3.
![]()
Além disso, o posto da matriz A’ também é 3, porque dentro dela existe uma submatriz 3×3 cujo determinante é diferente de 0. E não pode ser de posto 4 pois ‘não podemos fazer um determinante 4×4.
![]()
Portanto, aplicando o teorema de Rouché-Frobenius, sabemos que este é um sistema determinado compatível (SCD), pois o contradomínio de A é igual ao contradomínio de A’ e ao número de incógnitas.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Uma vez sabendo que o sistema é um SCD, aplicamos a regra de Cramer para resolvê-lo. Para fazer isso, lembre-se que a matriz A, seu determinante e a matriz A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5114be5e37d2c91f02f22fba22edc42_l3.png)
Para calcular x com a regra de Cramer, trocamos a primeira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b7402e02ee62bd78a6f880d3d122119_l3.png)
Para calcular a incógnita e com a regra de Cramer, trocamos a segunda coluna do determinante de A pela coluna de termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-551c66a9530d0195a9a4ff64d42350c4_l3.png)
Para calcular z com a regra de Cramer, trocamos a terceira coluna do determinante de A pela coluna dos termos independentes e dividimos pelo determinante de A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-28375ce522b7644a745a9adea4c78ae7_l3.png)
Portanto, a solução do sistema de equações para o caso m≠+1 e m≠-1 é:
![]()
m=+1:
Analisaremos agora o sistema quando o parâmetro m for igual a 1. Neste caso as matrizes A e A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6af272a99ed7c281ee8dd9199698686_l3.png)
Como vimos anteriormente, quando m=+1 o determinante de A é 0. Portanto a matriz A não é de posto 3. Mas dentro dela possui 2×2 determinantes diferentes de 0, por exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ebedf6c9e4316844dc99ceca9472fac5_l3.png)
Como a matriz possui um determinante de ordem 2 diferente de 0, a matriz A é de posto 2:
![]()
Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então agora tentamos, por exemplo, com o determinante das 3 últimas colunas:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d0109b155be9f87a0cee337ddec5517_l3.png)
Por outro lado, a matriz A’ contém um determinante 3×3 cujo resultado é diferente de 0, de modo que a matriz A’ é de posto 3:
![]()
Assim, quando m=+1 o posto da matriz A é menor que o posto da matriz A’. Assim, do teorema de Rouché-Frobenius, deduzimos que o sistema é um Sistema Incompatível (SI):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
Portanto, o sistema de equações não tem solução quando m=+1 , pois é um sistema incompatível.
m=-1:
Analisaremos agora o sistema quando o parâmetro m for -1. Neste caso as matrizes A e A’ são:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-46b0a00ef38d0e5a433b418de7eb1ec3_l3.png)
Como vimos anteriormente, quando m=-1 o determinante de A é 0. Portanto, a matriz A não é de posto 3. Mas dentro dela possui 2×2 determinantes diferentes de 0, por exemplo:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff5373c7e7901f253421efbbd52d192e_l3.png)
Como a matriz possui um determinante de ordem 2 diferente de 0, a matriz A é de posto 2:
![]()
Uma vez conhecida a classificação de A, calculamos a classificação de A’. Já sabemos que o determinante das 3 primeiras colunas dá 0, então agora tentamos, por exemplo, com o determinante das colunas 1, 3 e 4:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20](https://mathority.org/wp-content/ql-cache/quicklatex.com-a95e30910bd64db920f3c2bcb5f2ff62_l3.png)
Por outro lado, a matriz A’ contém um determinante 3×3 cujo resultado é diferente de 0, de modo que a matriz A’ é de posto 3:
![]()
Assim, quando m = -1, o posto da matriz A é inferior ao posto da matriz A’. Assim, do teorema de Rouché-Frobenius, deduzimos que o sistema é um Sistema Incompatível (SI):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
Portanto, o sistema de equações não tem solução quando m=-1 , pois é um sistema incompatível.