Matriz involucional - Matoridade

Nesta página você aprenderá o que é uma matriz involutiva. Também mostramos exemplos de matrizes involutivas de dimensões 2×2, 3×3 e 4×4. E finalmente, você encontrará a fórmula para uma matriz involucional.

O que é uma matriz involucional?

O significado da matriz involucional é o seguinte:

Definição de matriz involutiva : Uma matriz quadrada invertível cuja matriz inversa é a própria matriz.

$A^{-1} = A$

Ouro

$A$

é qualquer matriz e

$A^{-1}$

representa seu inverso.

Então obviamente uma matriz involucional é um exemplo de matriz regular ou não degenerada .

Se você não sabe o que é o inverso de uma matriz, pode ver aqui como calcular a matriz inversa 3×3 . É importante saber como inverter uma matriz, porém, para isso também é necessário saber como é calculado o adjunto de uma matriz .

Mas voltando ao assunto: quando uma matriz é involutiva, a multiplicação da matriz pela própria matriz dá a matriz identidade. Dê uma olhada na demonstração:

Qualquer matriz multiplicada por sua inversa fornece a matriz Identidade (ou Unidade). ENTÃO:

$\displaystyle A \cdot A^{-1} = I$

E como o inverso de uma matriz involucional é a própria matriz:

$\displaystyle A \cdot A = I$

Consequentemente, uma matriz involucional quadrada fornece a matriz identidade:

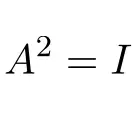
Exemplos de matrizes involucionais

Exemplo de uma matriz involutiva 2×2:

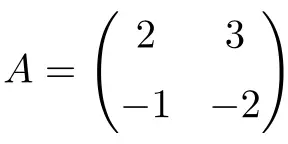
exemplo de uma matriz involutiva de dimensão 2x2

Podemos verificar que se trata de uma matriz involucional calculando a segunda potência da matriz:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Como a matriz A ao quadrado é a matriz identidade, a matriz A é uma matriz involucional 2×2.

Exemplo de uma matriz involutiva 3×3:

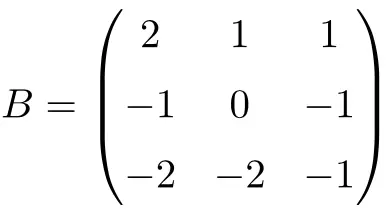
exemplo de uma matriz involutiva de dimensão 3x3

Podemos verificar que é uma matriz involucional resolvendo o produto da matriz por si só:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Como a matriz B ao quadrado é a matriz identidade, a matriz B é uma matriz involucional 3×3.

Exemplo de uma matriz involutiva 4×4:

A matriz Identidade (ou Unidade), qualquer que seja a sua dimensão, é por definição uma matriz involucional.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Podemos verificar que é uma matriz involucional elevando a matriz para 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Como a matriz identidade quadrada é a matriz identidade, a matriz identidade é uma matriz involucional 4×4.

Obviamente a matriz identidade pode ser de qualquer dimensão, pois é simplesmente uma matriz diagonal com todos os 1s na diagonal principal e o resto 0. Portanto a matriz identidade será sempre uma matriz involucional, qualquer que seja a sua ordem.

Fórmula de matriz involutiva

Uma das propriedades da matriz involucional é que sua fórmula pode ser conhecida. Mas a prova da fórmula de uma matriz involucional de segunda ordem é bastante tediosa, então deixaremos vocês direto ao resultado, é isso que realmente importa. Se você estiver mais interessado na demonstração, poderá vê-la explicada passo a passo abaixo nos comentários.

A fórmula para uma matriz involutiva de dimensão 2 × 2 é a seguinte:

Portanto, qualquer matriz cujos valores da diagonal principal sejam opostos e cujo determinante seja -1, será uma matriz involucional.

Porém, além das matrizes descritas por esta fórmula, deve-se levar em consideração que a matriz identidade e seu oposto também são matrizes involucionais de ordem 2:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Propriedades de uma matriz involutiva

As matrizes involucionais possuem as seguintes características:

O determinante de uma matriz involucional é sempre igual a -1 ou +1.

Existe uma relação entre matrizes involucionais e matrizes idempotentes : a matriz
$A$

é involucional se e somente se a matriz

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

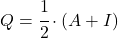
é idempotente.

Sim
$A$

E

$B$

são duas matrizes involucionais comutativas , então o produto da matriz

$AB$

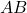
também é outra matriz involucional.

Qualquer potência de uma matriz involucional resulta em outra matriz involucional. Em particular, uma matriz involucional elevada a um expoente ímpar será igual a si mesma, por outro lado se for elevada a um expoente par será equivalente à matriz Identidade.

$A^2 = I$

$A^3 = A$