Nesta página explicamos o que são as partes de um monômio (coeficiente, parte literal, grau, etc.) e como identificá-las facilmente. Além disso, você poderá ver exemplos e até praticar com exercícios resolvidos passo a passo nas partes de um monômio.
Quais são as partes de um monômio?
As partes de um monômio são:
- Coeficiente : é o número que multiplica as variáveis (ou letras) do monômio.
- Variável : são cada uma das letras que aparecem no monômio.
- Parte literal : corresponde a todas as variáveis que formam o monômio com todos os seus expoentes.
- Grau : é a soma de todos os expoentes das variáveis monomiais.
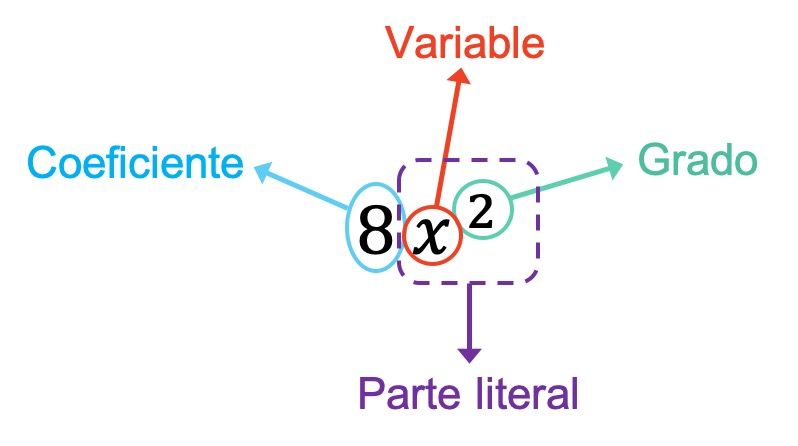
Como você pode ver no exemplo anterior, o coeficiente do monômio é 8 pois é o número que multiplica as variáveis. Além disso, neste caso, o monômio possui apenas uma variável, que é x. Portanto, a parte literal do monômio é formada por esta variável mais seu expoente, ou seja, x 2 . E finalmente, o monômio é de segundo grau porque o único expoente que possui é 2.
Por outro lado, uma das propriedades das partes de um monômio é que quando dois monômios têm a mesma parte literal, dizemos que são monômios semelhantes . Você pode aprender mais sobre este tipo de monômios na página vinculada, onde, entre outras coisas, é explicado porque eles são tão importantes para a matemática.
Exemplos de partes de monômios
Para que você entenda perfeitamente o conceito de partes de um monômio, deixamos vários exemplos:
Exemplo 1
![]()
- Coeficiente do monômio:
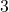
- Variáveis monomiais:
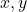
(neste caso, existem duas variáveis)
- Parte literal do monômio:
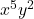
- Grau do monômio:
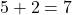
Exemplo 2
![]()
- Coeficiente do monômio:
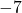
- Variáveis monomiais:
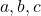
(neste caso, existem três variáveis)
- Parte literal do monômio:
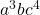
- Grau do monômio:
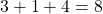
Tenha em mente que quando o expoente de uma variável não é definido, significa que ele é elevado a um e, portanto, na realidade o expoente dessa variável é 1 e não 0. Por este motivo, adicionamos uma unidade no cálculo de o grau deste monômio (3+ 1 +4=8), uma vez que
![]()
Se você estiver mais interessado, no link a seguir você poderá ver mais exemplos de monômios . Além disso, você poderá ver os diferentes tipos de monômios que existem, como é calculado o valor numérico de um monômio e qual a diferença entre um monômio e um polinômio.
Problemas resolvidos de partes de monômios
Por último, oferecemos-lhe vários exercícios para que possa verificar se compreendeu as diferentes definições das partes de um monômio.
Exercício 1
Quais são todas as partes do seguinte monômio?
![]()
Coeficiente do monômio:
![]()
Variáveis monomiais:
![]()
Parte literal do monômio:
![]()
Grau do monômio:
![]()
Exercício 2
Identifique todos os elementos do seguinte monômio:
![]()
Coeficiente do monômio:
![]()
Variáveis monomiais:
![]()
Parte literal do monômio:
![]()
Grau do monômio:
![]()
Exercício 3
Determine as partes do seguinte monômio com uma fração:
![]()
Coeficiente do monômio:
![]()
Variáveis monomiais:
![]()
Parte literal do monômio:
![]()
Grau do monômio:
![]()
Perfeito! Se você chegou até aqui, provavelmente já entende tudo sobre as partes de um monômio. É por isso que você está pronto para avançar para o próximo nível e aprender como fazer operações com monômios . Aqui você não apenas verá como são calculados todos os tipos de operações com monômios existentes, mas também verá como resolver operações combinadas com monômios e poderá praticar passo a passo com exercícios resolvidos.