Nesta página você encontrará tudo sobre vetores: o que são, suas características, como são calculados, como fazer operações com vetores, os diferentes tipos que existem,…
O que é um vetor?
A definição matemática de um vetor é a seguinte:
Em matemática, um vetor é um segmento direcionado que vai de um ponto (chamado de origem) a outro ponto (chamado de fim).
Por exemplo, no gráfico abaixo, você pode ver que o vetor
![]()
Tem o ponto A como origem e o ponto B como ponto final.
Os vetores são usados principalmente em matemática, particularmente em geometria e física, para representar graficamente forças vetoriais.
Características de um vetor
Depois de vermos qual é o significado matemático dos vetores, vamos agora ver quais são suas propriedades.
Cada vetor possui as seguintes características geométricas:
- Direção : A direção de um vetor é a direção da reta que contém o vetor ou de qualquer reta paralela a ele. Em outras palavras, a direção de um vetor é a reta sobre a qual ele se encontra.
- Direção : a direção de um vetor é a orientação do referido vetor, indicada por sua seta.
- Módulo (ou magnitude): o módulo de um vetor é o seu comprimento e corresponde ao valor numérico do vetor. Portanto, quanto maior o vetor significa, maior será a quantidade vetorial que ele representa.
- Ponto de aplicação : o ponto de aplicação de um vetor é a origem do referido vetor.
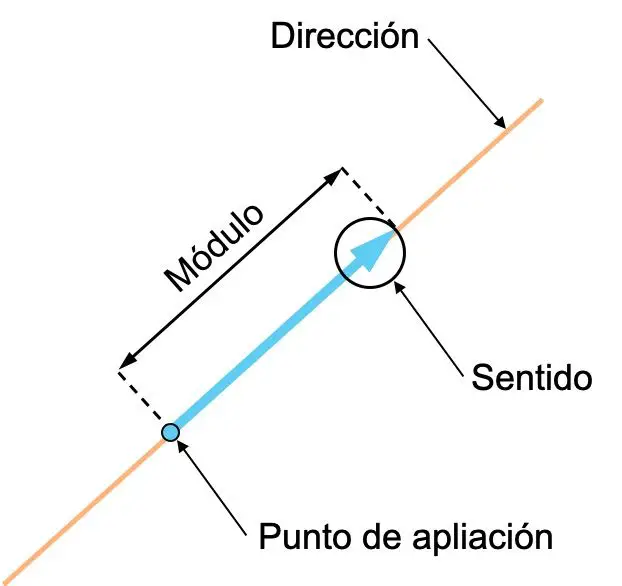
As noções de direção e sentido de um vetor são muitas vezes confusas, por isso é importante distinguir a diferença entre elas. Veja o exemplo a seguir com dois vetores, ambos têm a mesma direção, mas seus significados são diferentes:
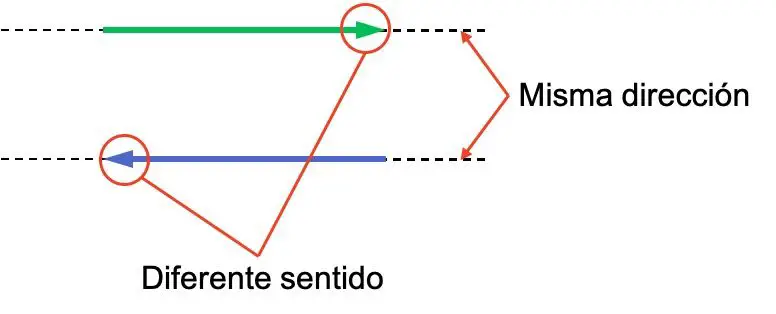
Os dois vetores têm a mesma direção porque são paralelos. Em vez disso, suas direções são opostas porque estão voltadas para trás.
Componentes de um vetor
Acabamos de ver que os vetores são representados graficamente por setas, mas os vetores também podem ser representados numericamente pelas componentes (ou coordenadas) de um vetor.
Por exemplo, se tivermos o seguinte vetor representado em um gráfico:
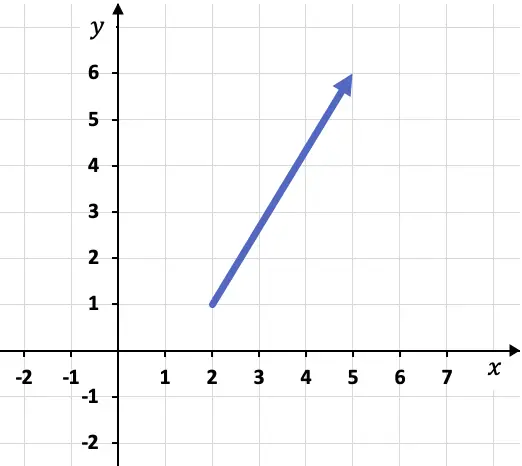
Para calcular as componentes do vetor, devemos primeiro identificar as coordenadas de sua origem e fim, ou seja, os pontos onde ele começa e onde termina. Neste caso, a origem e o fim do vetor são:
Origem do vetor: A(2,1)
Ponto final do vetor: B(5,6)
Então, para encontrar as coordenadas ou componentes do vetor, basta subtrair o ponto final menos a origem:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fba10729c8ded7f7c7051cfda5c12eab_l3.png)
Portanto, as componentes do vetor representado no gráfico são:
![]()
Operações vetoriais
adicionando vetor
Para somar numericamente dois vetores, você deve somar seus respectivos componentes. Ou em outras palavras, as coordenadas X dos dois vetores são somadas e iguais às coordenadas Y.
![]()
Para que você possa ver como isso é feito, adicionaremos os dois vetores a seguir:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24ac65138e4d395f7773aa19ba806a49_l3.png)
Dois vetores também podem ser adicionados a partir de suas representações gráficas. Para isso, normalmente utiliza-se a regra ou lei do paralelogramo, mas existem muitos métodos. Você pode ver exemplos e exercícios resolvidos sobre como adicionar dois vetores graficamente aqui.
subtração vetorial
Para subtrair analiticamente dois vetores, você deve subtrair seus respectivos componentes. Ou seja, as coordenadas X dos dois vetores são subtraídas uma da outra e iguais às coordenadas Y.
![]()
Como exemplo, subtrairemos os dois vetores a seguir:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5693a8287adebc3a4553358f8a8b0969_l3.png)
Assim como a adição, você também pode subtrair 2 vetores usando suas representações. Para isso, costuma-se utilizar a regra ou lei do triângulo, mas existem vários métodos. Você pode ver todos eles com exemplos e exercícios resolvidos sobre como subtrair dois vetores graficamente .
módulo de um vetor
Como vimos no início desta página, a norma de um vetor corresponde ao comprimento desse vetor. Bem, o comprimento (ou magnitude) de um vetor pode ser determinado a partir de seus componentes.
Considere qualquer vetor:
![]()
Para encontrar a magnitude de um vetor no plano, devemos aplicar a seguinte fórmula:
![]()
Por exemplo, calcularemos a magnitude do seguinte vetor usando a fórmula:
![]()
![]()
Embora pareça muito simples, determinar a magnitude de um vetor pode ser complicado. Se quiser ver mais exemplos e praticar com exercícios resolvidos do módulo de um vetor , recomendamos que visite esta página vinculada.
Multiplicação de um vetor por um escalar
Para calcular numericamente o produto de um vetor por um número (ou escalar), cada componente do vetor deve ser multiplicado por esse número.
![]()
No exemplo genérico a seguir você pode ver como a direção do vetor é mantida independentemente do sinal do escalar. Por outro lado, a direção do vetor depende do sinal do número que ele multiplica.

Abaixo você pode ver um exemplo numérico de como encontrar o produto de um vetor e um número:
![]()
![]()
Produto escalar
Na geometria analítica, o produto escalar é uma operação vetorial que multiplica dois vetores e os transforma em um número real.
Assim, a fórmula para o produto escalar de dois vetores é a seguinte:
![]()
Abaixo você tem um exemplo onde o resultado do produto escalar entre dois vetores é calculado:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2a8137101f391be2b197764b8b21223_l3.png)
Neste link você pode ver mais exemplos do produto escalar . Além disso, você encontrará outra forma de encontrar o produto escalar entre dois vetores, as propriedades desse tipo de operação com vetores e exercícios resolvidos passo a passo.
produto vetorial
Embora sejam muito semelhantes em nome, o produto escalar e o produto vetorial são completamente diferentes.
Produto vetorial , também chamado de produto vetorial, é uma operação entre dois vetores no espaço (em R3), ou seja, são vetores de três coordenadas.
Então, se tivermos dois vetores tridimensionais:
![]()
O produto vetorial dos dois vetores é igual ao resultado do seguinte determinante 3×3:
![]()
onde os vetores
![]()
são os vetores unitários nas direções dos eixos X, Y, Z, respectivamente.
Além disso, a direção do vetor resultante é perpendicular aos dois vetores multiplicados.
Como você pode imaginar, resolver esse tipo de operação é mais difícil que as anteriores e, por isso, temos uma página inteira com uma explicação detalhada de como é calculado o produto vetorial entre dois vetores. Portanto, caso tenha interesse, recomendamos que você o visite e pratique com os exercícios de produto vetorial resolvidos .
produto misto
O produto misto de três vetores, também chamado de produto escalar triplo, é uma multiplicação sucessiva entre três vetores envolvendo dois tipos diferentes de operações: o produto escalar e o produto vetorial. Portanto, a combinação das duas operações vetoriais dá um escalar (um número real).
Concretamente, o produto misto consiste em calcular o produto vetorial de dois vetores e, posteriormente, multiplicar vetorialmente o resultado obtido por um terceiro vetor. Veja a fórmula:
![]()
Tal como acontece com o produto vetorial, resolver o produto misto entre vetores não é fácil. Por isso recomendamos que você dê uma olhada nesta explicação do produto misto de três vetores , onde encontrará exemplos, exercícios resolvidos e o significado geométrico desta operação vetorial.
tipos de vetores
Existem muitos tipos diferentes de vetores, mas as definições mais importantes a saber são:
- Vetor unitário : vetor cujo módulo é igual a 1.
- Vetor fixo : Um vetor é fixo quando a origem do vetor é aplicada a um ponto fixo.
- Vetor livre : Um vetor é livre quando seu ponto de aplicação não está definido, mas é um ponto livre.
- Vetores colineares : dois ou mais vetores são colineares se compartilham a mesma linha de ação (linha onde o vetor está localizado).
- Vetores equivalentes : dois vetores são equipolênicos se tiverem o mesmo tamanho, mesmo sentido e mesma direção (embora possam ter diferentes pontos de aplicação).
- Vetores vinculados : Vetores vinculados são vetores equipólen que também atuam na mesma linha.
- Vetores opostos : dois vetores são opostos se tiverem a mesma magnitude e a mesma direção, mas uma direção diferente.
- Vetor posição : o vetor posição é o vetor cuja origem é o ponto (0,0) (origem das coordenadas).
- Vetores concorrentes : dois ou mais vetores são concorrentes quando suas linhas de ação passam pelo mesmo ponto, ou seja, se cruzam.
- Vetores paralelos : dois ou mais vetores são paralelos se tiverem a mesma direção, independentemente de suas direções.
- Vetores perpendiculares : Dois vetores são perpendiculares (ou ortogonais) quando suas direções formam um ângulo de 90º.
- Vetores ortonormais : Dois ou mais vetores são ortonormais se forem perpendiculares entre si e, além disso, forem unitários (sua magnitude é igual à unidade).
- Vetores coplanares : dois ou mais vetores são coplanares quando contidos no mesmo plano.
Ângulo entre dois vetores
Para encontrar o ângulo entre dois vetores dados, devemos aplicar a seguinte fórmula:
![]()
Ouro
![]()
E
![]()
são os módulos dos vetores
![]()
E
![]()
respectivamente.