Aqui você encontrará a explicação do que é a fórmula da equação canônica (ou segmentar) da reta, também chamada de equação simétrica. Além disso, você poderá ver exemplos e praticar com exercícios resolvidos. E, ainda, você descobrirá como a equação canônica é calculada a partir da equação geral (ou implícita) da reta.
Qual é a equação canônica ou segmentar da reta?
Lembre-se de que a definição matemática de uma reta é um conjunto de pontos consecutivos representados na mesma direção, sem curvas ou ângulos.
Assim, a equação canônica da reta , também chamada de equação segmentar da reta , é uma forma de expressar matematicamente qualquer reta. Para isso, basta conhecer os pontos de intersecção com os eixos coordenados da referida reta.
Por outro lado, em geometria analítica, a equação canônica (ou segmentar) da reta também é chamada de equação simétrica da reta .
Fórmula da equação canônica ou segmentar da reta
A equação canônica ou segmentar da reta é a expressão algébrica da reta que pode ser determinada conhecendo os valores onde a reta intercepta o eixo x e o eixo y.
Se uma linha intercepta os eixos cartesianos nos seguintes pontos:
Ponto de intersecção com o eixo X:
![]()
Ponto de intersecção com o eixo Y:
![]()
A fórmula para a equação canônica (ou segmentar) da reta é:
![]()

Deve-se notar que não existe equação canônica (ou segmentar) da reta em nenhum dos três casos a seguir:
- Quando a linha é vertical, ou seja, paralela ao eixo OY. Como a equação de uma reta vertical é

- Quando a linha é horizontal, ou seja, paralela ao eixo OX. Como a equação de uma reta horizontal é

- Quando a linha passa pela origem da coordenada (ponto
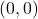
), pois teríamos então duas indeterminações na equação da reta.
Exemplo de como encontrar a equação canônica ou segmentar da reta
Para que você entenda melhor o conceito, resolveremos um problema de equação segmental (ou canônica) da reta:
- Encontre a equação canônica ou segmentar da reta que passa pelos dois pontos a seguir:
![]()
Neste caso, a declaração não nos dá 2 pontos, mas sim os dois pontos de intersecção com os eixos.
Ponto de intersecção da linha com o eixo X:
![]()
Ponto de intersecção da linha com o eixo Y:
![]()
Assim, como já conhecemos os dois pontos de intersecção com os eixos, basta aplicar a fórmula da equação canônica ou segmentar da reta:
![]()
E por fim, substituímos o valor dos parâmetros
![]()
E
![]()
na fórmula:
![]()
Agora você sabe qual é a equação canônica (ou segmentar) da reta. Porém, você deve saber que existem outras formas de expressar uma reta, e dentre elas se destaca a equação explícita . Este tipo de equação linear é difícil de entender completamente, por isso explicamos tudo sobre ela em detalhes na página do link.
Calcule a equação canônica ou segmentar da reta a partir de sua equação geral
Acabamos de ver uma maneira de determinar a equação canônica ou segmentar da reta, mas também existem outros métodos:
A equação canônica ou segmentar de uma reta pode ser obtida a partir da equação geral (ou implícita) desta mesma reta:
![]()
Primeiro, mudamos de lado no coeficiente C:
![]()
A seguir, dividimos a equação inteira pelo valor do parâmetro C com sinal alterado:
![]()
![]()
E, através das propriedades das frações, chegamos à fórmula da equação canônica ou segmentar da reta:
![]()
Portanto, segue-se desta fórmula que os termos
![]()
E
![]()
da equação canônica de uma reta são equivalentes às seguintes expressões:
![]()
Problemas resolvidos da equação canônica ou segmentar da reta
Exercício 1
Quais são os pontos de intersecção com os eixos coordenados da linha a seguir?
![]()
A reta do exercício é expressa na forma de uma equação canônica ou segmentar da reta, cuja fórmula é:
![]()
Portanto, os pontos onde a linha cruza os eixos coordenados são:
Ponto de intersecção com o eixo X:
![]()
Ponto de intersecção com o eixo Y:
![]()
Exercício 2
Qual é a equação canônica ou segmentar da linha representada graficamente?
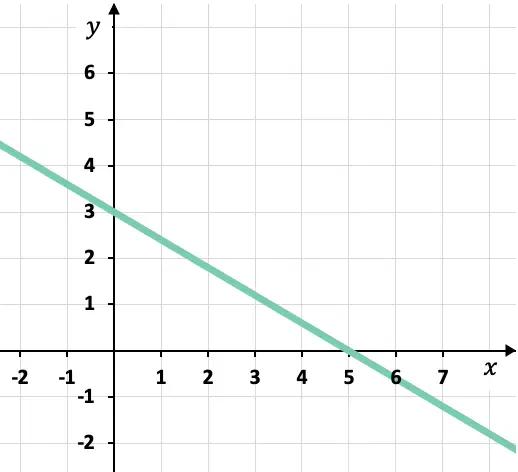
A partir do gráfico podemos saber os pontos onde a reta cruza os eixos coordenados:
Ponto de intersecção da linha com o eixo X:
![]()
Ponto de intersecção da linha com o eixo Y:
![]()
Assim, uma vez que já conhecemos os 2 pontos de intersecção com os eixos, basta utilizar a fórmula da equação canônica ou segmentar da reta:
![]()
E por fim, substituímos o valor dos parâmetros
![]()
E
![]()
na fórmula:
![]()
Exercício 3
Calcule a equação canônica ou segmentar da reta determinada pela seguinte equação geral (ou implícita):
![]()
Para passar de uma equação geral para uma equação segmental, devemos primeiro isolar o termo independente da equação:
![]()
![]()
Segundo, dividimos a equação inteira pelo coeficiente do lado direito da equação:
![]()
![]()
A expressão acima é equivalente ao seguinte:
![]()
Para que a equação canônica, segmentar ou simétrica da reta seja:
![]()
Exercício 4
Determine a equação canônica ou segmentar cujo vetor de direção é
![]()
e passa pelo ponto
![]()
Primeiro encontramos facilmente a equação contínua da reta a partir de seu vetor direção e um ponto que pertence à reta:
![]()
![]()
![]()
Agora vamos calcular a equação geral da reta multiplicando as frações transversalmente e agrupando os termos resultantes:
![]()
![]()
![]()
![]()
É, portanto, suficiente converter a equação geral da reta em uma equação canônica. Para fazer isso, primeiro excluímos o termo independente da equação:
![]()
A seguir, dividimos a equação inteira pelo coeficiente do lado direito da equação:
![]()
![]()
A expressão acima é equivalente ao seguinte:
![]()
Negativo dividido por negativo é igual a positivo:
![]()
As frações não podem ser mais simplificadas, portanto, a equação canônica, segmentar ou simétrica da reta é:
![]()