Aqui você encontrará as fórmulas para todos os tipos de equações da reta. Além disso, você poderá ver exemplos de como são calculadas e, além disso, praticar com exercícios resolvidos das equações da reta.
Quais são todas as equações da reta?
Lembre-se de que a definição matemática de uma reta é um conjunto de pontos consecutivos representados na mesma direção, sem curvas ou ângulos.
Assim, para expressar analiticamente qualquer reta no plano (em R2) utilizamos as equações da reta, e para encontrá-las basta um ponto pertencente à reta e o vetor diretor dessa reta. Com apenas esses dois elementos geométricos, você pode encontrar absolutamente todas as diferentes equações da reta, que são as seguintes:
As equações da reta são a equação vetorial, as equações paramétricas, a equação contínua, a equação implícita (ou geral), a equação explícita, a equação ponto-inclinação e a equação canônica (ou segmentar).
Todos os tipos de equações de reta têm o mesmo objetivo: representar matematicamente uma reta. Mas cada equação da reta tem suas propriedades e portanto, dependendo do problema, é melhor usar uma ou outra.

Depois de vermos o conceito de equações lineares, passamos agora a analisar as características de cada tipo de equação linear em particular. Abaixo você tem uma explicação detalhada dos diferentes tipos de equações da linha, mas se quiser pode ir diretamente para o final da tabela resumo com as fórmulas de todas as equações da linha .
Equação vetorial da reta
Sim
![]()
é o vetor de direção da linha e
![]()
um ponto que pertence à direita:
![]()
A fórmula para a equação vetorial da reta é:
![]()
Ouro:
-

E

são as coordenadas cartesianas de qualquer ponto da linha.
-

E

são as coordenadas de um ponto conhecido que faz parte da linha

-

E

são os componentes do vetor de direção da linha

-

é um escalar (um número real) cujo valor depende de cada ponto da reta.
É a equação vetorial da reta no plano, ou seja, quando se trabalha com pontos e vetores de 2 coordenadas (em R2). Porém, se estivéssemos fazendo cálculos no espaço (em R3), teríamos que adicionar um componente adicional à equação da reta:
![]()
Equações paramétricas da reta
As equações paramétricas de uma reta podem ser obtidas a partir de sua equação vetorial:
![]()
Primeiro multiplicamos o parâmetro
![]()
pelo vetor de direção da direita:
![]()
A seguir, adicionamos as coordenadas X e Y:
![]()
E, por fim, limpando cada variável separadamente, obtemos as equações paramétricas da reta:
![]()
Ouro:
-

E

são as coordenadas cartesianas de qualquer ponto da linha.
-

E

são as coordenadas de um ponto conhecido que faz parte da linha

-

E

são os componentes do vetor de direção da linha

-

é um escalar (um número real) cujo valor depende de cada ponto da reta.
Como antes, estas são as equações paramétricas da reta no plano (em R2), mas para encontrar as equações paramétricas da reta no espaço (em R3) seria necessário adicionar mais uma equação para a terceira variável Z:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e31f05449ce57a8af9ae4dda38535013_l3.png)
Equação contínua da reta
A equação contínua de qualquer reta pode ser deduzida de suas equações paramétricas:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-708dbb33878e2bab0dcc94c84f6ab670_l3.png)
Se limparmos a configuração
![]()
de cada equação paramétrica obtemos as seguintes expressões:
![]()
![]()
E Igualando as duas equações resultantes, obtemos a equação contínua da reta:
![]()
![]()
Resumindo, a equação contínua da reta é:
![]()
Ouro:
-

E

são as coordenadas cartesianas de qualquer ponto da linha.
-

E

são as coordenadas de um ponto conhecido que faz parte da linha

-

E

são os componentes do vetor de direção da linha

Esta fórmula é para a equação contínua da reta ao trabalhar em 2 dimensões (em 2D). Mas se estivéssemos realizando operações em 3 dimensões (3D), precisaríamos adicionar um componente adicional à equação da reta:
![]()
Equação implícita ou geral da reta
Sim
![]()
é o vetor de direção da linha e
![]()
um ponto que pertence à direita:
![]()
A fórmula para a equação implícita, geral ou cartesiana da reta é:
![]()
Ouro:
-

E

são as coordenadas cartesianas de qualquer ponto da linha.
- o coeficiente

é o segundo componente do vetor de direção da linha:

- o coeficiente

é o primeiro componente do sinal alterado do vetor de direção:

- o coeficiente

é calculado substituindo o ponto conhecido

na equação da reta.
a fórmula, a equação implícita de uma reta também pode ser obtida multiplicando as frações da equação contínua.
Equação explícita da reta
A fórmula para a equação explícita da reta é:
![]()
Ouro:
-

é a inclinação da linha.
-

sua interceptação em y, ou seja, a altura em que intercepta o eixo Y.
Na seção abaixo você verá como os parâmetros são determinados
![]()
E
![]()
da linha reta Mas, em particular, outra maneira de encontrar a equação explícita é usar a equação implícita; para isso, o desconhecido deve ser resolvido
![]()
da equação implícita.
Significado dos parâmetros m e n
Como vimos na definição da equação explícita da reta, o parâmetro
![]()
é a inclinação da linha e
![]()
sua interceptação em y. Mas o que isso significa? Vamos ver isso a partir da representação gráfica de uma linha:

O termo independente
![]()
é o ponto de intersecção da linha com o eixo do computador (eixo OY). Por exemplo, no gráfico acima
![]()
é igual a 1 porque a linha cruza o eixo y em y=1.
Por outro lado, o termo
![]()
indica a inclinação da linha , ou seja, sua inclinação. Como você pode ver no gráfico,
![]()
é igual a 2, pois a linha aumenta 2 unidades verticais para 1 unidade horizontal.
Obviamente, se a inclinação for positiva a função está aumentando (subindo), por outro lado se a inclinação for negativa a função está diminuindo (descendo).
Calcular a inclinação de uma reta
Depois de sabermos exatamente qual é a inclinação de uma reta, vamos ver como ela é calculada. Assim, existem 3 maneiras diferentes de determinar numericamente a inclinação de uma linha:
- Dados dois pontos diferentes na linha

E

A inclinação da linha é igual a:
- Sim

é o vetor de direção da reta, sua inclinação é:
- Sim

é o ângulo formado pela reta com o eixo das abcissas (eixo X), a inclinação da reta é equivalente à tangente desse ângulo:
![]()
![]()
![]()

Equação ponto-inclinação da reta
A fórmula para a equação ponto-inclinação da reta é:
![]()
Ouro:
-

é a inclinação da linha.
-

são as coordenadas de um ponto na linha

Equação canônica ou segmentar da reta
Embora esta variante da equação da reta seja menos conhecida, a equação canônica da reta pode ser obtida a partir dos pontos de intersecção da reta com os eixos cartesianos.
Sejam os dois pontos de intersecção com os eixos de uma determinada reta:
Corte com o eixo X:
![]()
Corte com eixo Y:
![]()
A fórmula para a equação canônica da reta é:
![]()

Em matemática, a equação canônica da reta também é chamada de equação segmentar ou equação simétrica.
Por outro lado, os coeficientes
![]()
E
![]()
Eles também podem ser encontrados a partir da equação geral da reta usando as seguintes fórmulas:
![]()
![]()
Todas as equações da reta (fórmulas)
Em resumo, aqui está uma tabela que mostra as fórmulas de todas as equações da reta:

Exemplo de cálculo de equações da reta
Agora que vimos toda a explicação da equação da reta, vamos ver como se resolve um problema típico de equações da reta:
- Encontre todas as equações da reta determinada pelo ponto

e o vetor
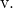
![]()
Em primeiro lugar, encontramos a equação vetorial da reta a partir de sua fórmula:
![]()
Basta substituir as coordenadas do ponto e do vetor na fórmula:
![]()
Em segundo lugar, encontramos as equações paramétricas da reta através de sua fórmula correspondente:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b4690a2ab033a4016f2d16b9554ddea_l3.png)
E também determinamos a equação contínua da reta com sua fórmula:
![]()
![]()
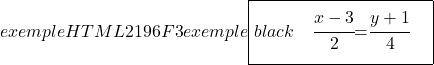
Como você viu, equações vetoriais, paramétricas e contínuas são fáceis de calcular, bastando utilizar suas respectivas fórmulas.
Vamos agora encontrar a equação geral (ou implícita) da reta. Para fazer isso, cruzamos as duas frações da equação contínua:
![]()
![]()
![]()
![]()
Agora podemos determinar a equação explícita da reta resolvendo a incógnita
![]()
da equação implícita:
![]()
![]()
![]()
![]()
Portanto, a inclinação da reta é igual a 2 (termo que acompanha a variável independente
![]()
).
![]()
E com isso podemos calcular a equação ponto-inclinação da reta com sua fórmula:
![]()
![]()
![]()
Por fim, para encontrar a equação segmentar da reta calculamos seus pontos de intersecção com os eixos OX e OY e depois aplicamos sua fórmula:
![]()
Ponto de intersecção com o eixo das abcissas (eixo X)
![]()
![]()
![]()
![]()
![]()
Ponto de intersecção com o eixo y (eixo Y)
![]()
![]()
![]()
![]()
![]()
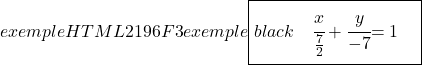
equação de reta passando por dois pontos
Outro problema muito comum em equações de reta é encontrar a equação da reta que é determinada por dois pontos dados. Embora possamos calcular o vetor direção da reta com os 2 pontos e depois a equação, a seguir fornecemos uma fórmula com a qual você pode encontrar direta e facilmente a equação dessa reta.
Considere dois pontos localizados em uma linha:
![]()
A fórmula para encontrar a equação da reta a partir de seus 2 pontos é:
![]()
Esta fórmula nos permite calcular diretamente a equação ponto-inclinação da reta quando temos 2 pontos pelos quais a reta passa.
Problemas resolvidos de equações da reta
Exercício 1
Encontre a equação vetorial, as equações paramétricas e a equação contínua da reta definida pelo ponto
![]()
e seu vetor diretor
![]()
Seja ambos:
![]()
Primeiro, calculamos a equação vetorial da reta a partir de sua fórmula:
![]()
![]()
Em seguida, encontramos as equações paramétricas da reta usando sua fórmula correspondente:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a734c32ae40ca816c19b895e54916eb4_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-bff16cf5ab85c87d8a866a2d74ea2a31_l3.png)
E, por fim, determinamos a equação contínua da reta com sua respectiva fórmula:
![]()
![]()
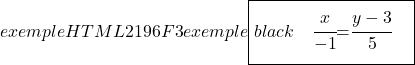
Exercício 2
Encontre a equação implícita, a equação explícita e a equação ponto-inclinação da reta determinada pelo ponto
![]()
e seu vetor de direção é
![]()
![]()
A fórmula para a equação implícita da reta é:
![]()
Devemos, portanto, encontrar os coeficientes A, B e C. As incógnitas A e B são obtidas a partir das coordenadas do vetor diretor da reta, pois sempre se verifica a seguinte igualdade:
![]()
Consequentemente, o coeficiente A é a segunda coordenada do vetor, e o coeficiente B é a primeira coordenada do sinal alterado do vetor:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9357fbcba6acde824f0fa1cc3e389a0c_l3.png)
Portanto, só precisamos encontrar o coeficiente C. Para isso, devemos substituir o ponto que sabemos que pertence à reta em sua equação:
![]()
![]()
![]()
![]()
![]()
Portanto, a equação implícita, geral ou cartesiana da reta é:
![]()
Agora podemos determinar a equação explícita da reta resolvendo a incógnita
![]()
da equação implícita:
![]()
![]()
![]()
![]()
Portanto, a inclinação da reta é igual a 3 (termo antes da variável independente
![]()
).
![]()
E, a partir do valor da inclinação da reta, podemos calcular a equação ponto-inclinação da reta com sua fórmula:
![]()
![]()
![]()
Exercício 3
Determine 3 pontos na seguinte reta, expressos como uma equação implícita ou geral:
![]()
Para calcular um ponto numa reta, precisamos simplesmente atribuir um valor a uma das variáveis e depois encontrar o valor da outra variável nesse ponto.
Calculamos um primeiro ponto fazendo
![]()
![]()
![]()
![]()
![]()
![]()
Encontramos então um segundo ponto dando outro valor à variável
![]()
Por exemplo
![]()
![]()
![]()
![]()
![]()
![]()
![]()
E, finalmente, calculamos um terceiro ponto resolvendo
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Exercício 4
Encontre todas as equações da reta definida pelo ponto
![]()
e o vetor
![]()
![]()
Em primeiro lugar, encontramos a equação vetorial da reta a partir de sua fórmula:
![]()
![]()
Em segundo lugar, encontramos as equações paramétricas da reta através de sua fórmula correspondente:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3bf46da9a68147118874a619f918077_l3.png)
E também determinamos a equação contínua da reta usando sua fórmula:
![]()
![]()
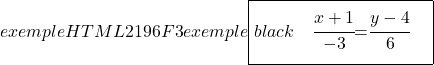
Vamos agora prosseguir para encontrar a equação implícita ou geral da reta. Para fazer isso, cruzamos as duas frações da equação contínua:
![]()
![]()
![]()
![]()
Agora podemos determinar a equação explícita da reta resolvendo a incógnita
![]()
da equação implícita:
![]()
![]()
![]()
![]()
Portanto, a inclinação da reta é equivalente a -2 (termo que acompanha a variável independente
![]()
).
![]()
E com isso podemos calcular a equação ponto-inclinação da reta com sua fórmula:
![]()
![]()
![]()
Por fim, para encontrar a equação segmentar da reta, calculamos os pontos de intersecção da reta com os eixos OX e OY e depois utilizamos sua fórmula:
![]()
Ponto de intersecção com o eixo das abcissas (eixo X)
![]()
![]()
![]()
![]()
![]()
Ponto de intersecção com o eixo y (eixo Y)
![]()
![]()
![]()
![]()
![]()
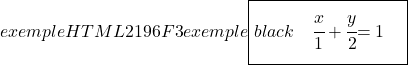
Exercício 5
Encontre a equação da reta que passa pelos dois pontos a seguir:
![]()
Como já conhecemos dois pontos na reta, aplicamos diretamente a fórmula da equação da reta a 2 pontos dados:
![]()
Agora substituímos as coordenadas cartesianas dos pontos na fórmula:
![]()
E, finalmente, calculamos a inclinação da reta:
![]()
![]()
A equação da reta que passa por esses dois pontos é, portanto:
![]()