Nesta página você descobrirá o que significa quando duas linhas são coplanares. Você também poderá ver quando duas retas são coplanares e, além disso, encontrará exemplos e exercícios resolvidos de retas coplanares.
O que são duas linhas coplanares?
Na geometria analítica, a definição de linhas coplanares é a seguinte:
Duas retas são coplanares quando estão no mesmo plano. Portanto, retas coplanares só podem ser retas secantes , retas paralelas ou retas coincidentes .
Além disso, duas linhas coplanares são suficientes para definir completamente um plano. Embora obviamente um plano possa ter mais de duas retas coplanares, na verdade todo plano contém um número infinito de retas.
Por outro lado, se duas retas não são coplanares, isso significa que elas se cruzam.
Exemplos de linhas coplanares
Para que você entenda melhor o conceito de retas coplanares, aqui está um exemplo com três retas:
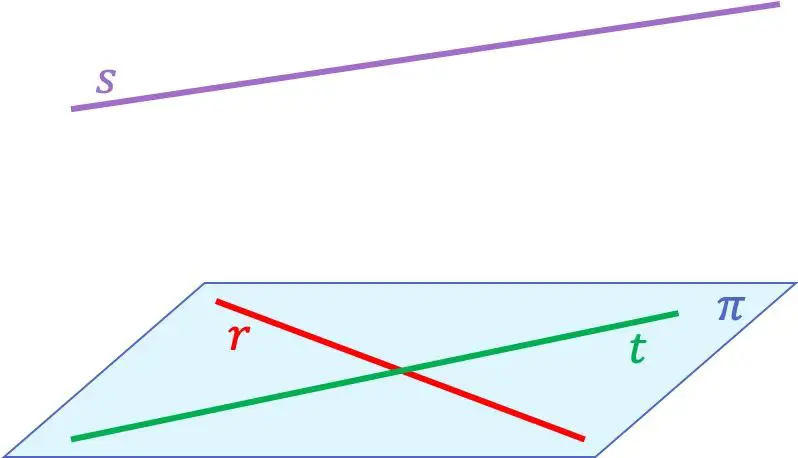
Neste caso, as linhas
![]()
E
![]()
Eles são coplanares porque pertencem ao mesmo plano. Em vez disso, a linha reta
![]()
não é coplanar com nenhuma das outras duas linhas, uma vez que intercepta as linhas
![]()
E
![]()
Como você sabe se duas linhas são coplanares?
Como vimos acima na explicação das retas coplanares, estas só podem ser retas secantes, paralelas ou coincidentes. Em outras palavras, 2 linhas cruzadas nunca serão coplanares.
Portanto, para saber se duas retas são coplanares, deve-se determinar a posição relativa entre elas, e se são duas retas que se cruzam, paralelas ou coincidentes, isso significa que são retas coplanares.
Assim, para verificar a coplanaridade de duas retas, primeiro é necessário saber calcular a posição relativa de duas retas no espaço . Se ainda não está familiarizado com este conceito, o melhor é que primeiro consulte o link, onde encontrará a explicação completa, bem como exemplos, exercícios e problemas resolvidos.
Exercício resolvido de linhas coplanares
Como exemplo, resolveremos um exercício típico sobre retas coplanares:
- Determine se as duas linhas a seguir são coplanares ou não:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=4t \\[1.7ex] z=5 \end{cases} \qquad \qquad s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76e57f7dd2bfa67f2cf4eb2ee0455dcf_l3.png)
A primeira coisa que devemos fazer é encontrar a posição relativa entre as duas retas e, para isso, devemos ter ambas expressas com o mesmo tipo de equação. Então cruzaremos a linha reta
![]()
da equação geral (ou implícita) às equações paramétricas:
![Rendered by QuickLaTeX.com \displaystyle s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases} \xrightarrow{x \ = \ t} \ \begin{cases} 2t+y=0 \\[1.7ex] z=-2\end{cases} \longrightarrow \ \begin{cases} x=t \\[1.7ex] y=-2t \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8dbc805cb7e0020c9c82c90e56e011_l3.png)
Portanto, o vetor de direção de cada linha é:
![]()
As coordenadas dos vetores de direção das duas retas são proporcionais, portanto só podem ser retas coincidentes ou paralelas. Portanto, neste caso particular não há necessidade de calcular a posição relativa exata, uma vez que as linhas paralelas e as linhas coincidentes são linhas coplanares. Portanto as duas retas são coplanares .