Aqui você descobrirá como calcular o ponto de simetria em relação a outro ponto, em relação a uma reta e em relação a um plano. Além disso, você poderá ver exemplos e exercícios resolvidos passo a passo.
Ponto simétrico a outro ponto
Antes de vermos como o ponto simétrico é calculado, vamos revisar o que exatamente é um ponto simétrico em relação a outro ponto:
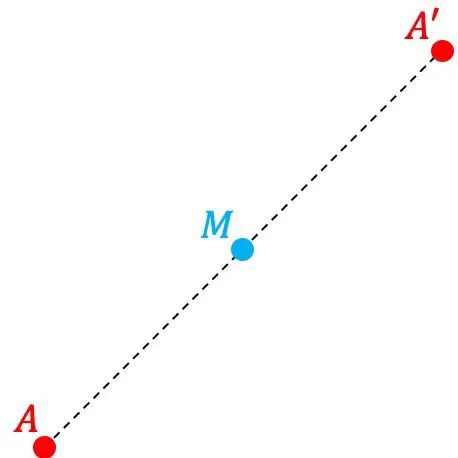
O ponto A’ é o ponto simétrico do ponto A em relação a outro ponto M se o ponto A’ estiver localizado simetricamente à mesma distância do ponto M que a distância entre os pontos A e M. Portanto, M é o ponto médio do segmento formado por pontos A e A’.
![]()
Por outro lado, dizemos também que o ponto M é o centro de simetria.
Assim, para calcular as coordenadas do ponto de simetria, utilizaremos a fórmula do ponto médio de um segmento :
![]()
Desta equação extraímos o ponto desconhecido A’ e obtemos a fórmula para o ponto simétrico em relação a outro ponto:
![]()
Exemplo de encontrar o ponto simétrico em relação a outro ponto
Como exemplo, calcularemos o ponto de simetria do ponto A em relação ao ponto M. Considere os dois pontos:
![]()
Para determinar o ponto de simetria entre esses dois pontos, aplicamos a fórmula do ponto de simetria em relação a outro:
![]()
Agora substituímos os pontos na fórmula:
![]()
E operamos:
![]()
![]()
ponto simétrico a uma linha reta
Acabamos de ver a noção de um ponto que é simétrico em relação a outro ponto. Bem, o ponto simétrico de um ponto em relação a uma reta é muito semelhante:
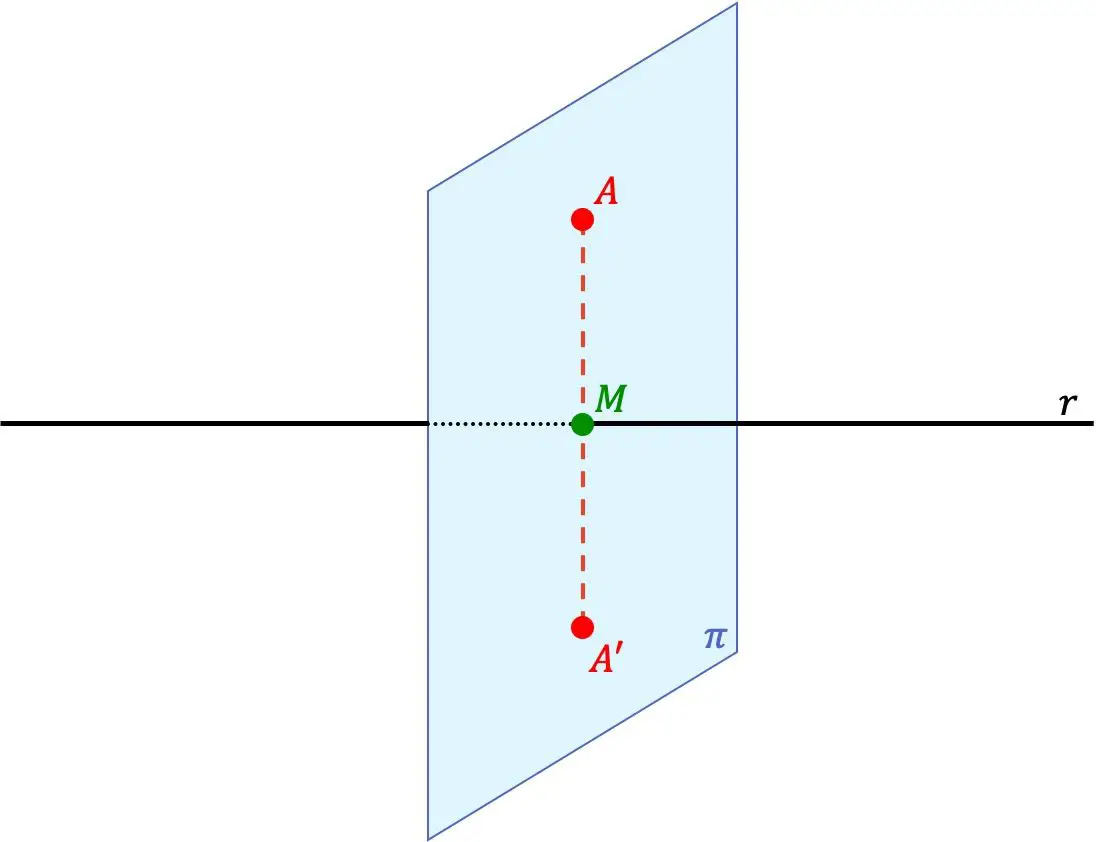
O ponto A’ é o ponto simétrico do ponto A em relação a uma reta se os dois pontos A’ e A estão na mesma reta perpendicular à reta e, além disso, a distância entre o ponto A’ e a reta é igual à distância entre o ponto A e a reta.
![]()
Portanto, a reta r também é um eixo de simetria entre os pontos.
Assim, para determinar o ponto de simetria do ponto A em relação à reta r , devemos seguir o seguinte procedimento:
- Encontramos o plano perpendicular à reta r que passa pelo ponto A (plano π da representação gráfica anterior). Para isso, devemos utilizar o vetor direção da reta, que será o vetor normal do plano.
- Calculamos o ponto de intersecção entre o plano encontrado e a reta (ponto M na imagem anterior).
- Usamos a fórmula ponto sobre ponto simétrico (vista na seção acima) para encontrar o ponto simétrico do ponto A em relação ao ponto M. O resultado é o ponto simétrico que procurávamos.
Exemplo de cálculo do ponto de simetria em relação a uma reta
Assim que soubermos calcular o ponto de simetria de outro ponto em relação a uma reta, veremos um exercício resolvido como exemplo:
- Encontre o ponto simétrico do ponto A em relação à linha r. Sendo dito ponto e linha:
![Rendered by QuickLaTeX.com \displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5906f8f5fce95109f9f19d93d1f41cd_l3.png)
Primeiro, precisamos calcular o plano perpendicular à reta r que passa pelo ponto A. O vetor normal a este plano será o vetor diretor da reta, cujos componentes são os termos na frente do parâmetro
![]()
porque é expresso na forma de equações paramétricas:
![]()
E os coeficientes A, B e C da equação de um plano coincidem com as coordenadas do seu vetor normal, portanto:
![]()
O ponto A deve estar neste plano, então podemos agora substituir o ponto A na equação do plano para encontrar o coeficiente D:
![]()
![]()
![]()
![]()
![]()
Portanto, a equação do plano perpendicular à reta ry que passa pelo ponto A é:
![]()
Depois de conhecermos a equação do plano, precisamos calcular o ponto de intersecção do plano e da reta. Para fazer isso, substituímos as coordenadas da reta na equação do plano e resolvemos a equação resultante:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd611c8a6c7e516dbb67583b49f0b8e6_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Agora substituímos o valor de
![]()
obtido na equação da reta:
![Rendered by QuickLaTeX.com \displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b0c515e3969169679e810db65a99e3f_l3.png)
Portanto, o ponto de intersecção entre a reta r e o plano perpendicular a ela é:
![]()
Finalmente, basta encontrar o ponto simétrico do ponto A em relação ao ponto M; para isso, podemos utilizar a fórmula vista no início desta página:
![Rendered by QuickLaTeX.com \begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4b39555d71f045dd42e9422dd077679_l3.png)
ponto simétrico a um plano
Antes de vermos o método de determinação do ponto de simetria de outro ponto em relação a um plano, vejamos qual é a sua definição:
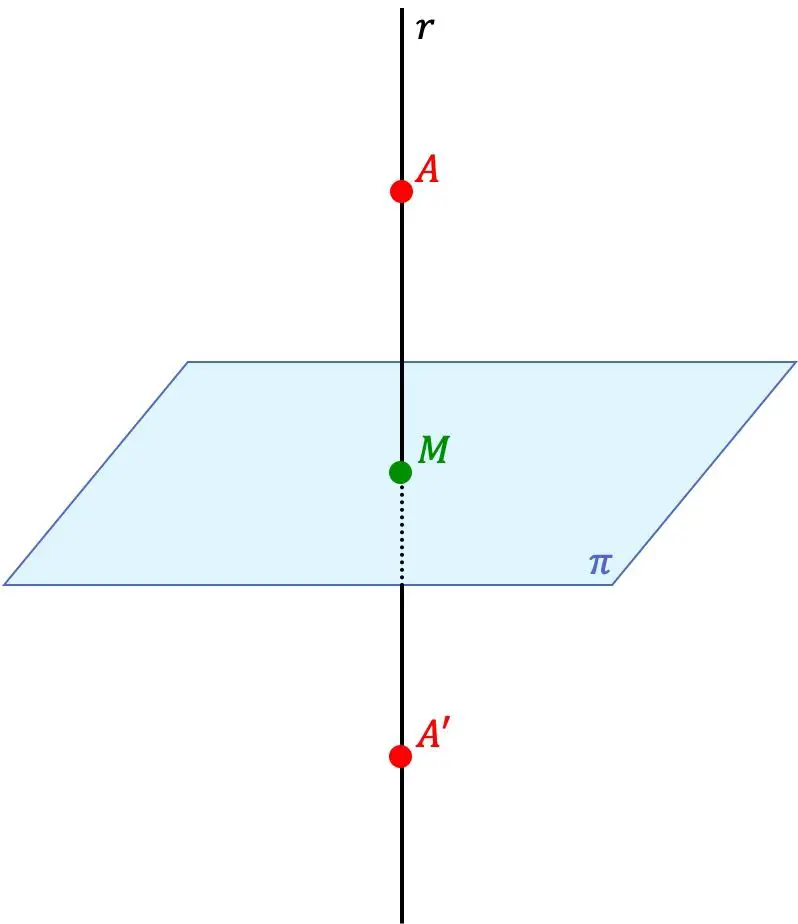
O ponto A’ é o ponto simétrico do ponto A em relação a um plano se os dois pontos A’ e A estão na mesma linha perpendicular ao plano e, além disso, a distância entre o ponto A’ e o plano é equivalente à distância entre o ponto A e o plano.
![]()
Portanto, o plano também é um plano de simetria entre os dois pontos.
Assim, para conhecer as coordenadas cartesianas do ponto simétrico do ponto A em relação ao plano π, deve-se seguir os seguintes passos:
- Encontramos a equação da reta perpendicular ao plano que passa pelo ponto A. Para isso usaremos o vetor normal ao plano como vetor diretor da reta.
- Calculamos o ponto de intersecção entre o plano e a reta encontrada (ponto M da imagem anterior).
- Usamos a fórmula ponto sobre ponto simétrico (vista na seção inicial) para encontrar o ponto simétrico do ponto A em relação ao ponto M. O resultado é o ponto simétrico que procurávamos.
Exemplo de determinação do ponto de simetria em relação a um plano
Abaixo você pode ver um problema resolvido referente ao ponto de simetria de outro ponto em relação a um plano:
- Determine o ponto de simetria de A em relação ao plano π. Tendo dito ponto e plano:
![]()
A primeira coisa que precisamos fazer é encontrar a equação da reta perpendicular ao plano e que passa pelo ponto A. Para isso, podemos usar o vetor normal ao plano como vetor diretor da reta, cujas componentes X, Y, Z são os coeficientes dos termos A, B e C respectivamente da equação do plano:
![]()
Podemos agora construir as equações paramétricas da reta ortogonal ao plano com o vetor diretor encontrado e um de seus pontos (ponto A):
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ec51a68802f626dcd5cf7a3bc1dda59_l3.png)
Uma vez conhecida a reta perpendicular, calculamos o ponto de intersecção do plano e da reta substituindo as coordenadas da reta na equação do plano:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb4ee2c7f6742eec2e1fa11cac3c5635_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Agora substituímos o valor de
![]()
obtido na equação da reta:
![Rendered by QuickLaTeX.com \displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a9373141f2f699971d5789e1cb0ed0d_l3.png)
Portanto, o ponto de intersecção entre o plano e a reta perpendicular é:
![]()
Por fim, só precisamos encontrar o ponto simétrico do ponto A em relação ao ponto M. E, para isso, podemos usar a fórmula vista no início desta página:
![Rendered by QuickLaTeX.com \begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e8199cf83bc3bdfbf0a7b2adb65a97af_l3.png)