Esta página explica as diferentes posições relativas que existem entre uma linha e um círculo. Além disso, você poderá ver como encontrar a posição relativa entre uma linha e um círculo.
Quais são as posições relativas de uma linha e de um círculo?
Na geometria analítica, a posição relativa de uma reta em relação a um círculo só pode ser exterior, tangente ou secante:
- Exterior : quando a distância entre a linha e o centro do círculo é maior que o raio.
- Tangente : quando a distância entre a reta e o centro do círculo é igual ao raio.
- Secante : quando a distância entre a linha e o centro do círculo é menor que o raio.
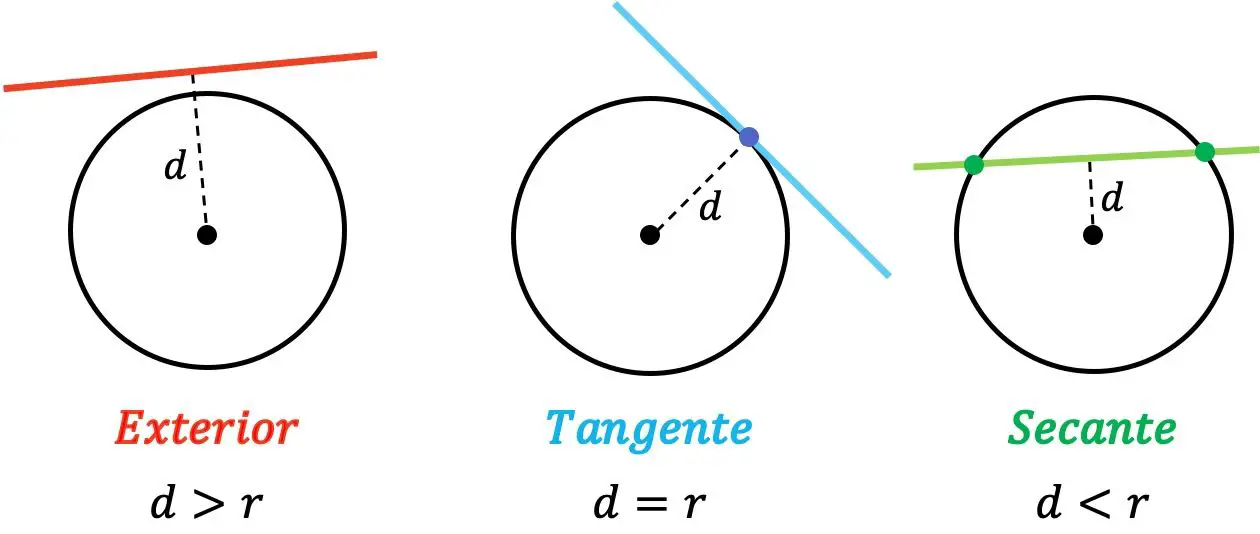
Portanto, se uma linha estiver fora de um círculo, ela não o interceptará em nenhum ponto. Por outro lado, quando a reta é tangente à circunferência, as duas têm um ponto em comum. E, finalmente, uma reta é secante a uma circunferência quando a interseta em dois pontos diferentes.
Como determinar a posição relativa entre uma linha e um círculo?
Existem duas maneiras de encontrar a posição relativa de uma reta em relação a um círculo no plano: uma calculando a distância entre a reta e o centro do círculo, e a outra resolvendo um sistema composto de equações da equação de a reta e a equação da circunferência.
A seguir, veremos exatamente o que é cada método.
Método 1: Distância entre a linha e o centro do círculo
Como vimos na explicação do conceito de posição relativa entre uma reta e um círculo, a distância entre uma reta e o centro de um círculo indica que tipo de posição relativa se trata.
Este método consiste, portanto, em encontrar a distância entre a linha e o centro do círculo. Obviamente, para poder fazer isso você deve saber calcular a distância entre um ponto e uma reta , nesta página você poderá ver como fazê-lo, além de exemplos e exercícios resolvidos para praticar.
Então, dependendo do resultado da distância obtida, será um caso ou outro:
- A linha estará fora do círculo se a distância obtida for maior que o raio do círculo.
- A reta será tangente ao círculo se a distância obtida for equivalente ao raio do círculo.
- A linha cruzará o círculo se a distância obtida for menor que o raio do círculo.
Método 2: resolver um sistema de equações
Outra maneira de encontrar a posição relativa de uma reta em um círculo é usar um sistema de equações formado pela equação da reta e pela equação do círculo. Obviamente, para aplicar este método você precisa saber qual é a equação da circunferência e qual é a fórmula da equação da reta .
Dependendo do número de soluções do sistema de equações, estaremos diante de um caso ou outro:
- Se o sistema de equações não tiver solução, significa que a reta e o círculo não têm um ponto comum, portanto a reta está fora do círculo.
- Se o sistema de equações tem 1 solução, isso implica que a reta e o círculo têm um ponto comum, portanto a reta é tangente ao círculo.
- Se o sistema de equações tiver 2 soluções, isso significa que a reta e a circunferência têm dois pontos em comum, portanto a reta é secante à circunferência.