Neste artigo explicamos o que são funções contínuas e como determinar se uma função é contínua num ponto ou não. Além disso, você encontrará propriedades de funções contínuas e análises de continuidade das funções mais comuns. Finalmente, você pode praticar com exercícios resolvidos sobre a função contínua para compreender totalmente o conceito.
O que é uma função contínua?
A continuidade de uma função pode ser estudada graficamente. Uma função contínua é uma função que pode ser representada em um gráfico sem tirar o lápis do papel.
Função contínua
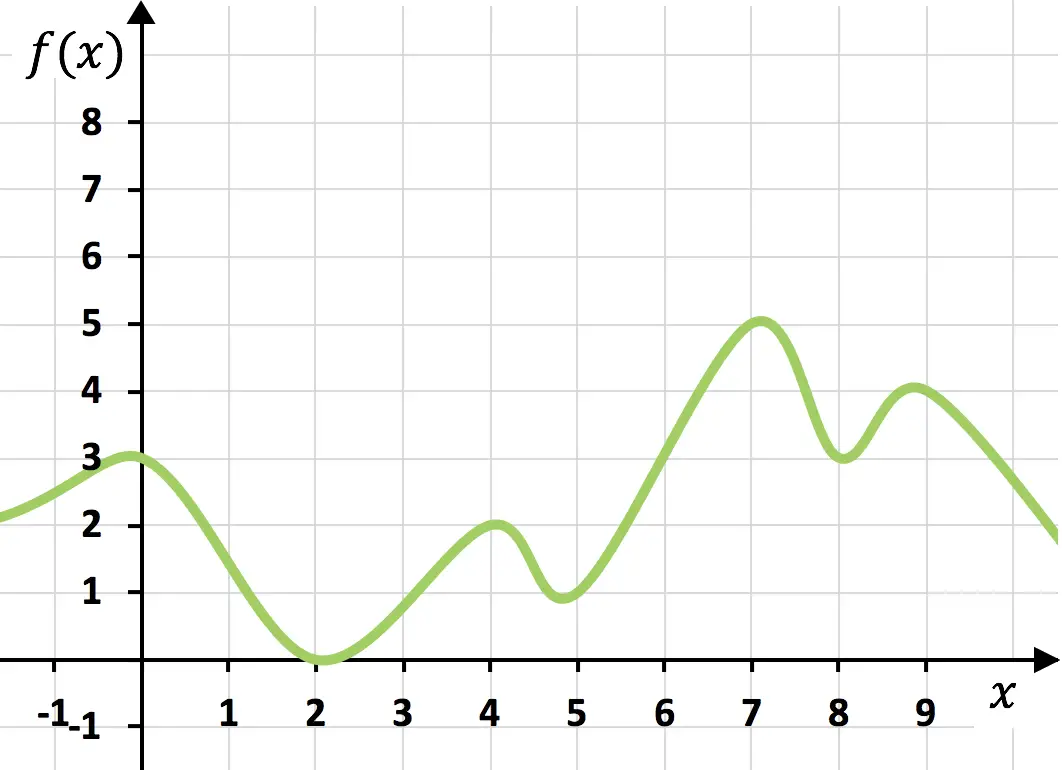
A função acima é contínua porque pode ser desenhada de uma só vez, sem levantar a mão do papel.
Por outro lado, quando a condição de continuidade anterior não é colocada numa função, diz-se que é uma função descontínua .
Função descontínua
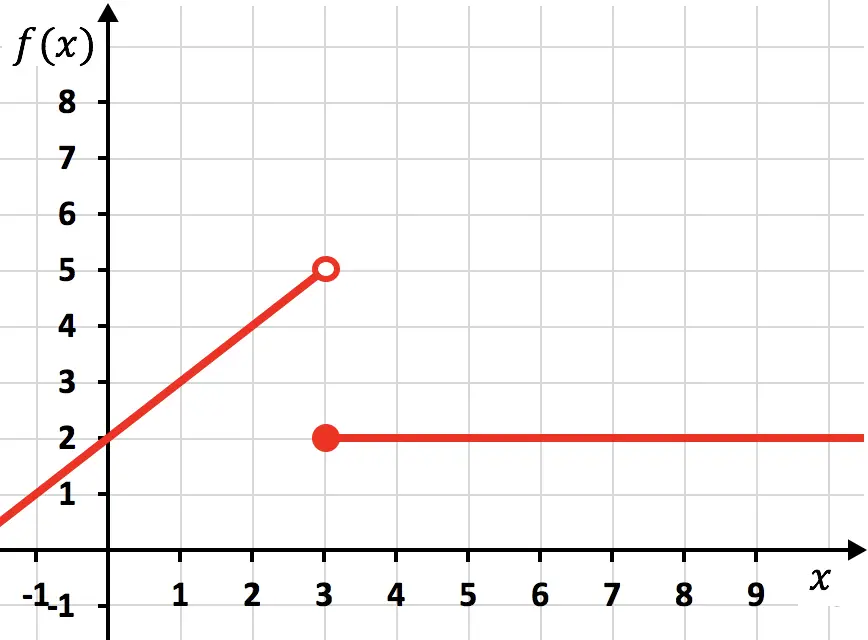
A função anterior é descontínua porque para representá-la é necessário fazer duas linhas com o lápis. Neste caso, a função deixa de ser contínua em x=3, dizemos portanto que x=3 é um ponto de descontinuidade .
Além disso, existem três tipos de descontinuidades : descontinuidade evitável, descontinuidade inevitável de salto finito e descontinuidade inevitável de salto infinito. No link a seguir você pode ver como é cada tipo de descontinuidade e o que há de diferente em cada uma delas:
➤ Veja: tipos de descontinuidades
Continuidade de uma função em um ponto
Depois de vermos a aparência do gráfico de uma função contínua, veremos como saber se uma função é contínua ou não analiticamente.
Matematicamente, uma função é contínua em um ponto se as três condições a seguir forem atendidas:
- A função existe neste ponto, ou seja, existe a imagem do ponto.
- Existe o limite da função neste ponto. Portanto, os limites laterais esquerdo e direito da função neste ponto são iguais.
- A imagem do ponto coincide com o limite da função neste ponto.
![]()
![]()
![]()
Assim, se as três condições de continuidade forem satisfeitas em todos os pontos de uma função, a função é contínua.
Como exemplo, analisaremos a continuidade da seguinte função por partes:

Mesmo se você mudar de seção, no ponto
![]()
A função é contínua, pois os limites laterais da função neste ponto são iguais e coincidem mais com o valor da função neste ponto.
![]()
Por outro lado, a função não é contínua no ponto
![]()
porque os dois limites laterais são diferentes e, portanto, o limite da função não existe neste ponto:
![]()
Resumindo, a função definida pelas peças é contínua em todos os números reais, exceto em
![]()
onde há uma descontinuidade.
Também podemos verificar que a função é descontínua em
![]()
pois para representá-lo graficamente é necessário retirar o lápis do papel neste momento.
Continuidade de funções elementares
Certos tipos de funções são contínuas pelas suas características:
- As funções constantes são contínuas em todos os números reais.
![]()
- As funções polinomiais são contínuas para todos os números reais.
![]()
- As funções racionais (ou fracionárias) são contínuas em todos os números reais exceto em valores que anulam o denominador da fração, nestes pontos a função apresenta uma descontinuidade.
![]()
- As funções exponenciais são contínuas sobre todos os números reais:
![]()
- As funções logarítmicas são contínuas em todos os pontos que tornam seu argumento positivo.
![]()
- A continuidade das funções irracionais , ou funções com raízes, depende do índice do radical (n). Se o índice for par, estas são funções contínuas em todos os pontos que tornam o argumento raiz igual ou maior que zero. Mas se o índice for ímpar, são funções contínuas em todos os números reais.
![]()
- A continuidade das funções trigonométricas depende do tipo de função. A função seno e a função cosseno são contínuas no conjunto dos números reais, mas a função tangente é descontínua nos pontos
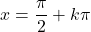
(onde k é um número inteiro).
![]()
Propriedades de funções contínuas
Sean
![]()
E
![]()
duas funções contínuas no ponto
![]()
Próximo:
- A soma de duas funções contínuas num ponto é outra função contínua nesse ponto.
![]()
- O produto de duas funções contínuas num ponto é igual a outra função contínua nesse ponto.
![]()
- A divisão de duas funções contínuas num ponto resulta em outra função contínua nesse ponto, desde que esse ponto não cancele a função de divisão.
![]()
- A composição de duas funções contínuas num ponto dá origem a uma função contínua neste mesmo ponto.
![]()
➤ Veja: o que é uma função composta?
Exercícios resolvidos sobre a continuidade de uma função
Exercício 1
Encontre as descontinuidades da função mostrada no gráfico a seguir. Determine também que tipo de descontinuidade é.
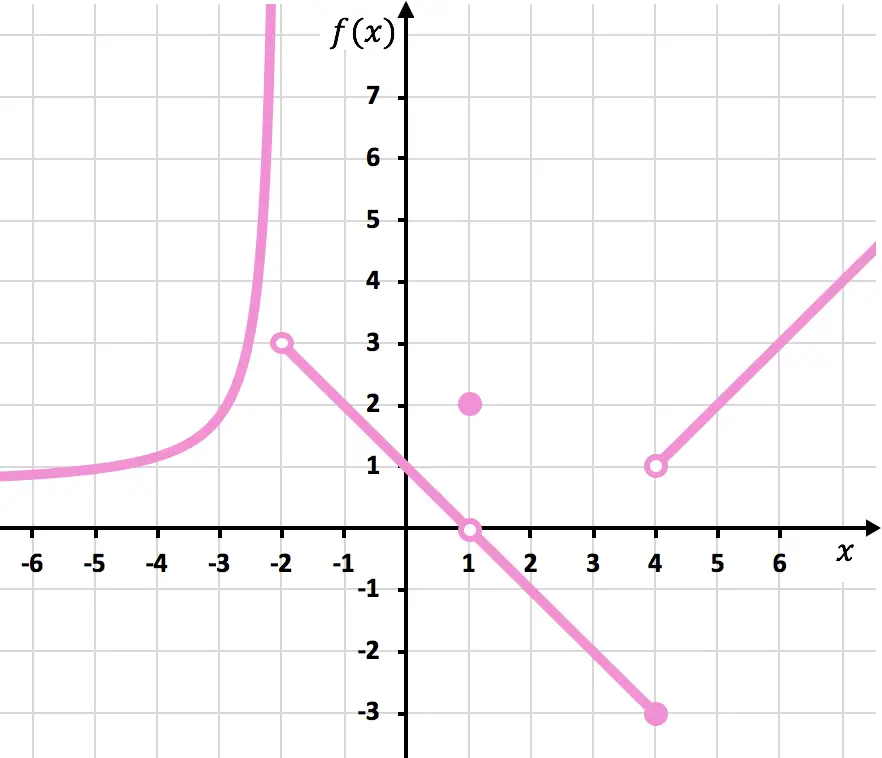
Nota: para realizar este exercício recomendamos que veja primeiro quais são os diferentes tipos de descontinuidades e como são identificadas. Você pode ver a explicação no link do princípio dos tipos de descontinuidade .
Para desenhar a função você deve levantar o lápis em x=-2, em x=1 e em x=4. A função é, portanto, descontínua nestes três pontos.
Em x=-2, o limite do lado esquerdo é +∞ e o limite do lado direito é 3. Assim, como um dos limites laterais é infinito, a função tem uma inevitável descontinuidade de salto infinito em x=-2.
![]()
O limite da função em x=1 é 0 e, por outro lado, o valor da função em x=1 é igual a 2. A função apresenta portanto uma descontinuidade evitável em x=1.
![]()
![]()
Em x = 4, o limite do lado esquerdo é -3 e o limite do lado direito é 1. Portanto, como os dois limites laterais são diferentes e nenhum deles dá infinito, a função inevitavelmente tem uma descontinuidade de salto finita em x =4.
![]()
Exercício 2
Determine os pontos nos quais a função mostrada no gráfico a seguir é descontínua.
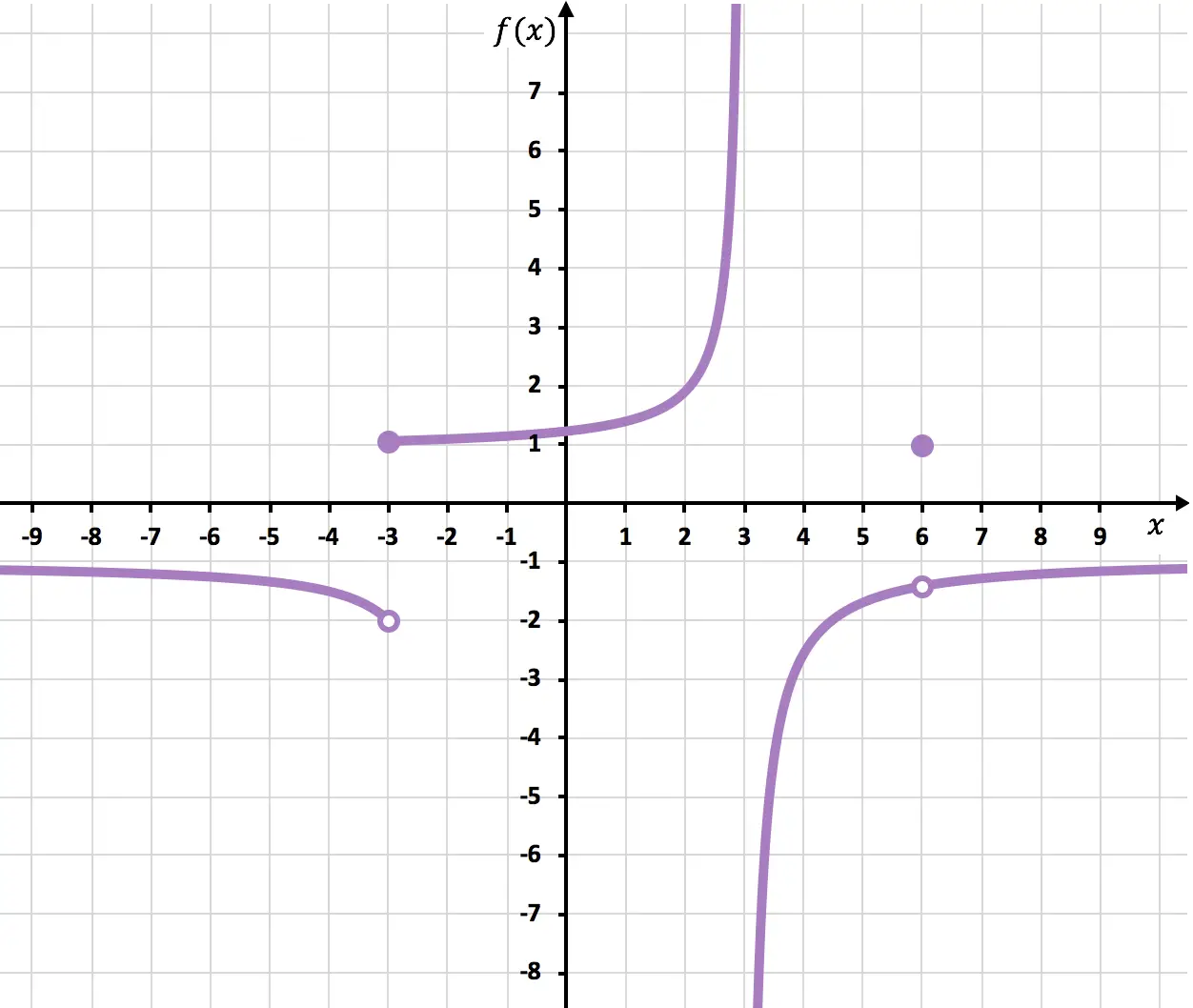
No ponto x=6 a função é interrompida porque existe um ponto aberto. O limite quando x se aproxima de 6 é -1,4 mas f(6)=1. A função, portanto, tem uma descontinuidade evitável em x=6 porque o valor do limite não coincide com o valor da função:
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4](https://mathority.org/wp-content/ql-cache/quicklatex.com-33612be383c71fea04c8c886710f7f10_l3.png)
![]()
Em x=-3 os limites laterais não coincidem e nenhum dá o infinito. A função, portanto, tem uma inevitável descontinuidade de salto finito em x=-3.
![]()
E finalmente, a função tem uma inevitável descontinuidade de salto infinito em x = 3, uma vez que pelo menos um limite lateral neste ponto resulta no infinito.
![]()
Exercício 3
Analise a continuidade da seguinte função racional:
![]()
As funções racionais são contínuas em todo o seu domínio, ou seja, em todos os números reais, exceto nos valores que cancelam o denominador. Portanto, igualamos o denominador da função racional a zero para ver quais pontos não pertencem ao domínio:
![]()
![]()
![]()
A função será, portanto, contínua em todos os pontos, exceto x=5.
Exercício 4
Analise a continuidade da seguinte função por partes:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a18e6289d268e6ea9fe1ee3ea14d31fd_l3.png)
A função também é contínua na primeira seção,
![]()
, como na segunda seção,
![]()
, uma vez que são funções polinomiais.
Portanto, o único ponto em que a função pode ser descontínua é o ponto em que a função se quebra por partes. Então vamos calcular os limites laterais neste ponto:
![]()
![]()
Os dois limites laterais coincidem portanto, o limite da função quando x tende a 1 é igual a 3:
![]()
Além disso, a imagem de x=1 também é 3:
![]()
Assim, como o limite da função em x=1 é igual à imagem do referido ponto, a função é contínua no ponto x=1. E, portanto, é contínuo em todos os números reais.
![]()
Exercício 5
Estude a continuidade da seguinte função irracional:
![]()
É uma função radical com índice par, portanto a função será contínua enquanto o argumento do radical for maior que 0 (porque a raiz quadrada de um número negativo não existe):
![]()
Resolvemos a desigualdade:
![]()
![]()
![]()
A solução consiste em todos os números maiores ou iguais a -3. A função é, portanto, contínua no intervalo de seu domínio:
![]()
Exercício 6
Analise a continuidade da seguinte função logarítmica:
![]()
Esta é uma função logarítmica e não existe o logaritmo de um número negativo nem o logaritmo de 0. Portanto, a função existirá enquanto o argumento do logaritmo for positivo (maior que zero):
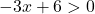 Resolvemos a desigualdade:
Resolvemos a desigualdade:
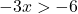
![]()
Lembre-se de que ao dividir um número negativo pelo outro lado de uma inequação, você deve inverter o sinal da inequação.
![]()
A solução consiste em todos os números menores que 2. O domínio de definição da função é, portanto:
![]()
A função é, portanto, contínua em todos os pontos do seu domínio.
Exercício 7
Calcule a continuidade da seguinte função:
![]()
No denominador da fração temos um radical com índice par, portanto a função existirá sempre que o conteúdo da raiz for igual ou maior que zero:
![]()
Mas também, a raiz está no denominador da fração, e o denominador de uma fração nunca pode ser 0. Portanto, a função só existirá se o conteúdo da raiz for estritamente maior que 0:
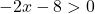 Agora resolvemos a desigualdade:
Agora resolvemos a desigualdade:
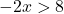
![]()
Lembre-se de que quando mudamos os lados de um número negativo multiplicando ou dividindo uma inequação, devemos também girar o sinal de inequação.
![]()
O resultado são todos os números menores que -4. Assim, o domínio da função e, portanto, a sua continuidade, são definidos pelo seguinte intervalo:
![]()
Exercício 8
Calcule o valor de k para que a função seja contínua em todo
![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7d8f0d6e0730c139c3baff0989a8fe7_l3.png)