Nesta página você encontrará tudo sobre a parábola: o que é, o que representa, seus elementos (foco, diretriz, vértice, etc.) sua equação (com os diferentes tipos de equações da parábola), exemplos, exercícios resolvidos, suas propriedades, suas aplicações,…
O que é uma parábola?
A parábola é um conceito que possui significados muito diferentes, mas sua definição matemática é a seguinte:
Em matemática, uma parábola é o lugar geométrico dos pontos no plano que são equidistantes de um ponto fixo (chamado de foco) e de uma linha fixa (chamada de diretriz).
Portanto, qualquer ponto de uma parábola está à mesma distância do seu foco e da sua diretriz.

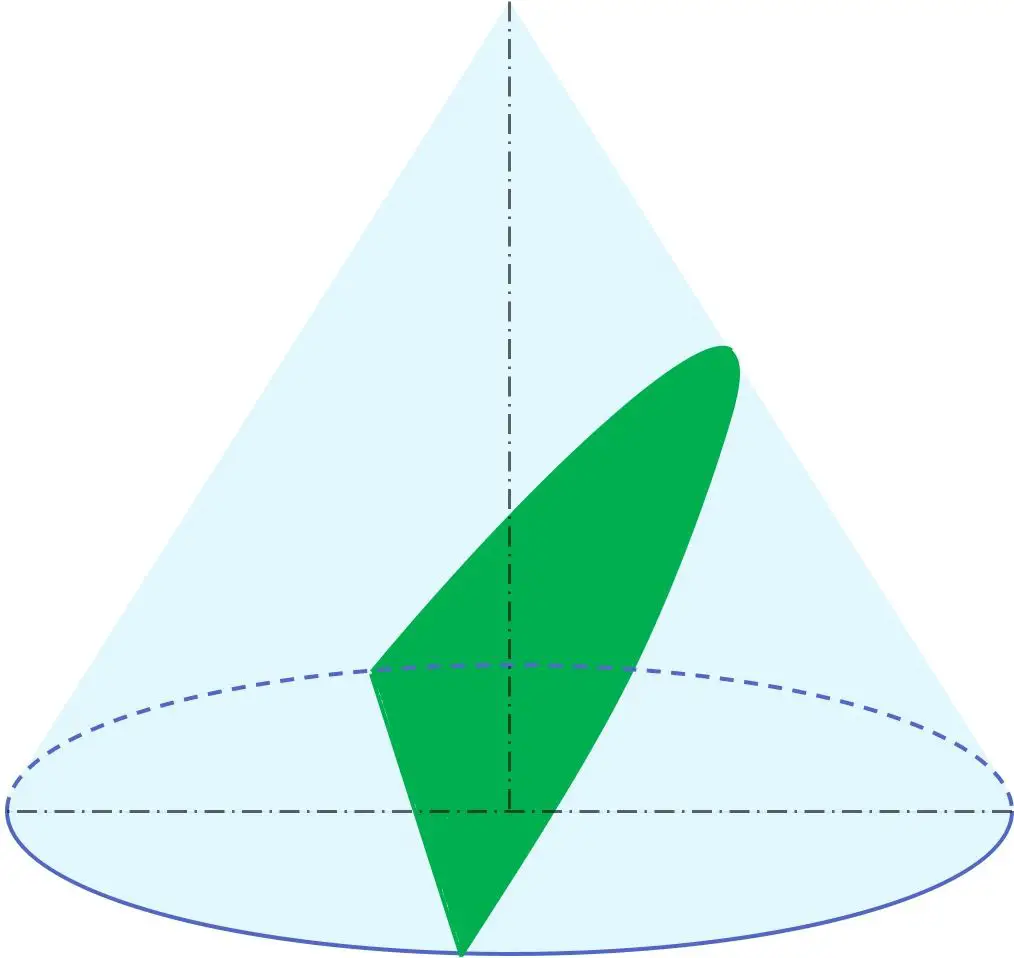
Além disso, em geometria, a parábola é uma das seções cônicas junto com a circunferência, a elipse e a hipérbole. Em outras palavras, uma parábola pode ser obtida a partir de um cone.
Em particular, a parábola resulta da secção de um cone por um plano com um ângulo de inclinação em relação ao eixo de revolução equivalente ao ângulo do gerador do cone. Portanto, o plano que contém a parábola é paralelo ao gerador do cone.
Elementos de uma parábola
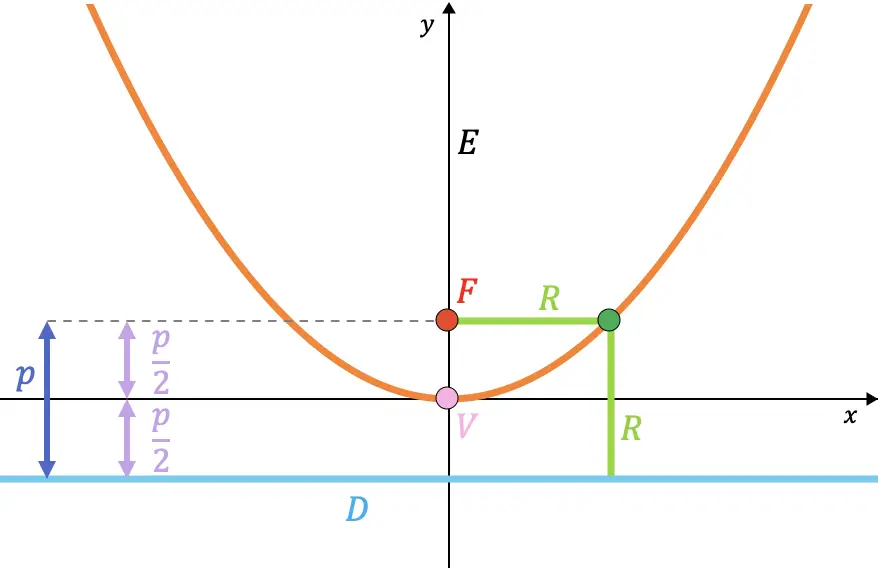
As características de uma parábola dependem dos seguintes elementos:
- Foco (F) : é um ponto fixo dentro da parábola. A distância de qualquer ponto da parábola ao foco é igual à distância deste mesmo ponto à diretriz da parábola.
- Diretriz (D) : é uma reta fixa exterior à parábola. Um ponto da parábola está à mesma distância da diretriz e do foco da parábola.
- Parâmetro (p) : é a distância do foco ao diretor.
- Vetor raio (R) : é o segmento que une um ponto da parábola ao foco. Seu valor coincide com a distância do ponto à diretriz.
- Eixo (E) : é a reta perpendicular à diretriz que passa pelo foco e é o eixo de simetria da parábola, no gráfico abaixo corresponde ao eixo do computador (eixo Y). Também chamado de eixo focal.
- Vértice (V) : é o ponto de intersecção entre a parábola e seu eixo.
- Distância focal : é a distância entre o foco e o vértice, ou entre a diretriz e o vértice. Seu valor é sempre igual a
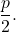
lado direito
O lado direito de uma parábola é a corda dentro da parábola que passa pelo foco e é paralela à diretriz.
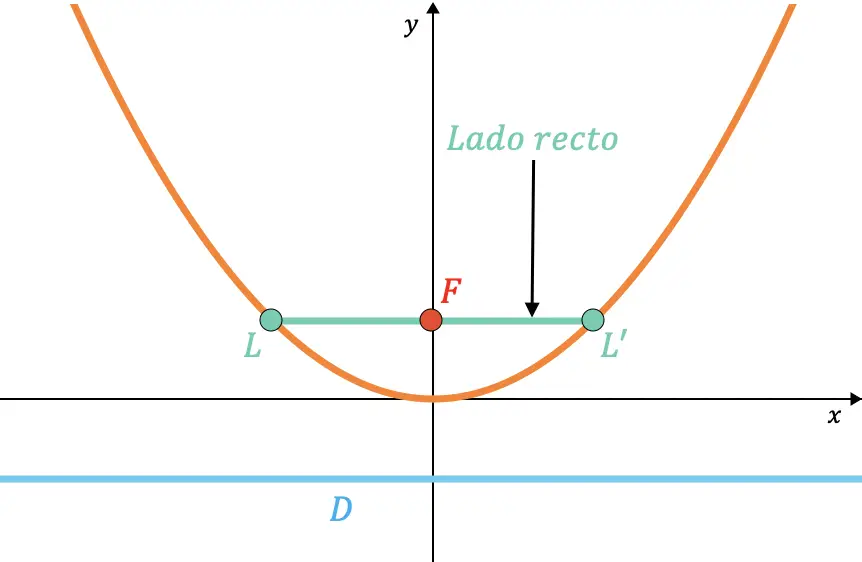
Da mesma forma, pode-se mostrar que o comprimento do lado direito é sempre o dobro do valor do parâmetro
![]()
![]()
Por outro lado, as duas retas tangentes à parábola que passam pelas extremidades do lado direito formam um ângulo de 45º com o próprio lado direito e também se cruzam no topo da parábola.
equações de parábola
A equação de uma parábola é um tipo de função quadrática porque deve sempre ter pelo menos 1 termo quadrado. Além disso, a equação de uma parábola depende da sua orientação horizontal ou vertical.
Assim, na geometria analítica, existem várias maneiras de expressar matematicamente uma parábola: a equação canônica ou reduzida , a equação ordinária e a equação geral da parábola.
Equação reduzida ou canônica da parábola
O que diferencia a equação reduzida ou canônica das demais equações parabólicas é que o vértice da parábola é a origem das coordenadas , ou seja, o ponto (0,0).
A forma da equação reduzida da parábola depende se ela é horizontal ou vertical. Observe a seguinte representação gráfica onde estão indicadas as 4 variantes possíveis:
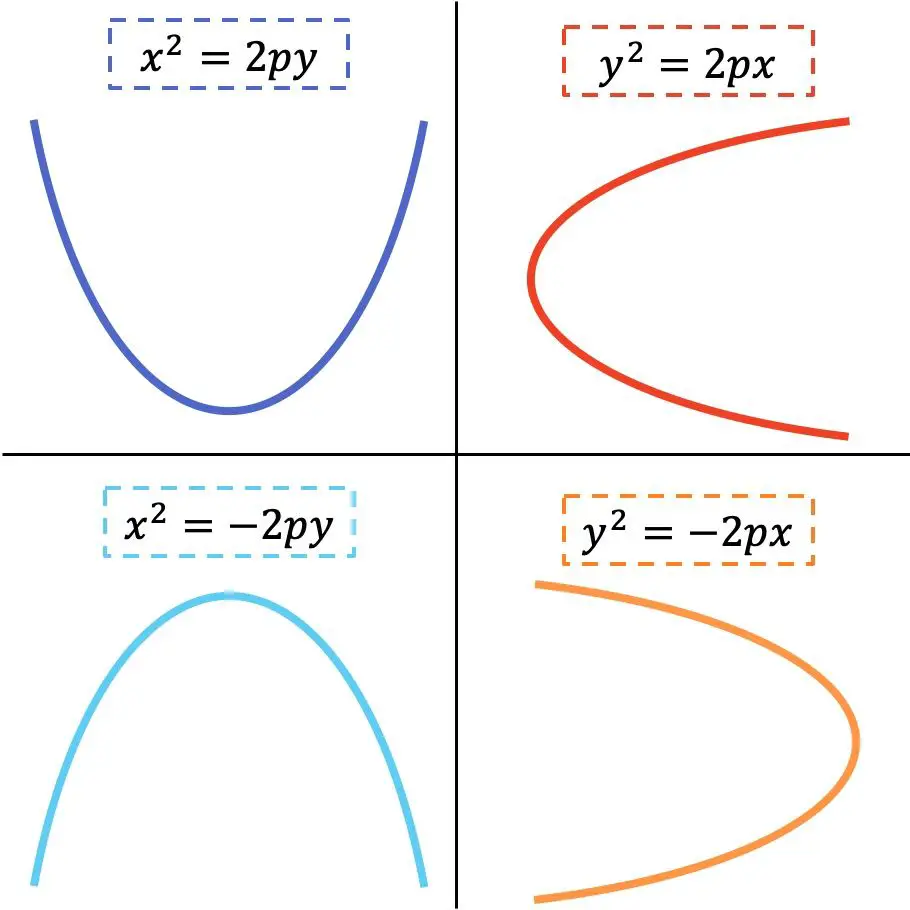
Ouro
![]()
é o parâmetro característico da parábola.
Como você pode ver na imagem anterior, quando a variável x é elevada ao quadrado, a parábola é vertical, por outro lado, quando a variável y é elevada ao quadrado, a parábola é horizontal. Por outro lado, a direção dos ramos da parábola depende do sinal da equação.
Equação ordinária da parábola
Acabamos de ver como fica a equação da parábola quando seu vértice ou centro corresponde à origem das coordenadas (a equação reduzida ou canônica), mas qual é a equação da parábola se o vértice está fora da origem?
Quando o vértice da parábola é um ponto qualquer, utilizamos a equação ordinária da parábola , cuja expressão é:
![]()
onde o centro ou vértice da parábola é o ponto
![]()
A equação anterior corresponde à parábola orientada verticalmente, ou seja, o eixo focal da parábola é paralelo ao eixo Y.
Da mesma forma, para definir uma parábola orientada horizontalmente (seu eixo focal é paralelo ao eixo X), devemos utilizar a seguinte variante da equação ordinária da parábola:
![]()
Onde, como antes, o centro ou vértice da parábola é o ponto
![]()
Equação geral da parábola
Até agora, todas as equações de parábolas que analisamos são usadas para expressar parábolas horizontais ou verticais. Mas obviamente uma parábola também pode ser oblíqua ou inclinada .
Bom, para expressar esse tipo de parábola, utilizamos a equação geral da parábola , cuja fórmula é a seguinte:
![]()
A equação acima é uma parábola se e somente se os coeficientes
![]()
E
![]()
não são simultaneamente zero e, além disso, a seguinte condição é atendida:
![]()
Exemplo de como encontrar o vértice, foco e diretriz de uma parábola a partir de sua equação
Em muitos exercícios e problemas de parábola, você é solicitado a calcular o vértice, o foco e a diretriz de uma determinada parábola. Portanto, vamos ver como isso é feito através de um exemplo:
- Encontre o vértice, o foco e a diretriz da seguinte parábola:
![]()
O fundamental para resolver este tipo de problema de parábola é determinar o parâmetro p da parábola . Neste caso, a equação da parábola corresponde à equação reduzida ou canônica (parábola vertical):
![]()
Portanto, o parâmetro p é:
![]()
![]()
![]()
Por outro lado, como a parábola segue a equação reduzida ou canônica, isso significa que seu vértice ou centro está na origem das coordenadas:
![]()
Depois de conhecermos o vértice e o valor do parâmetro da parábola, podemos facilmente encontrar seu foco e diretriz.
O termo quadrático da equação é a variável x para que o eixo da parábola seja paralelo ao eixo OY e, de fato, como seu vértice é o ponto (0,0), o eixo da parábola será o OY próprio eixo. Então, o foco de uma parábola está sempre localizado no eixo da parábola e a uma distância de
![]()
do topo da parábola, então suas coordenadas são:
![]()
![]()
![]()
Da mesma forma, a diretriz será a linha horizontal que está a uma distância
![]()
do vértice da parábola, que é a origem das coordenadas. A equação da reta será, portanto:
![]()
![]()
![]()
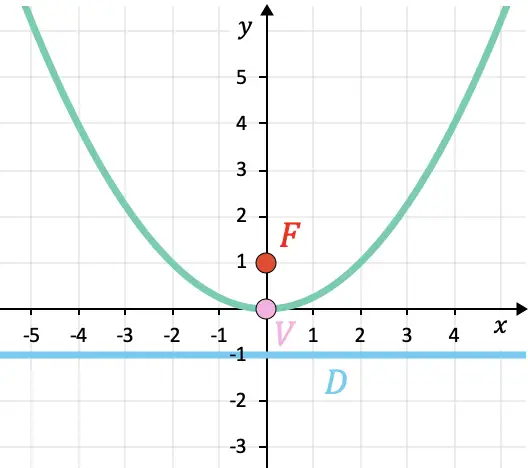
A parábola foi representada graficamente abaixo para que você possa verificar os resultados:
Propriedades das parábolas
Todas as parábolas têm as seguintes propriedades:
- Uma parábola é uma curva aberta, ou seja, é composta por dois ramos sem pontos em comum que se estendem de forma ilimitada.
- Cada parábola possui um único eixo de simetria, onde está localizado o vértice da referida parábola.
- Uma parábola orientada verticalmente é convexa quando seus ramos sobem; pelo contrário, a parábola é côncava se os seus ramos forem para baixo.
- A excentricidade de uma parábola é equivalente à unidade (1). A excentricidade é um coeficiente que neste caso é calculado dividindo a distância do foco ao centro da parábola pela distância do vértice à diretriz (e as duas distâncias sempre coincidem em seu valor).
- Da propriedade anterior segue-se que todas as parábolas são semelhantes ou semelhantes.
- Uma parábola não tem assíntotas.
aplicações parabólicas
Agora que você está familiarizado com o significado de uma parábola, você pode estar se perguntando… qual é o sentido de uma parábola?
Bom, mesmo que não lhe pareça, a forma geométrica de uma parábola é muito comum na vida real. Por exemplo, muitas vezes ao lançar uma bola ela faz um movimento parabólico, principalmente no basquete. Bem, a equação da parábola é muito útil para estudar analiticamente a trajetória parabólica que a bola segue.
Outra aplicação da antena parabólica diz respeito a antenas (daí o nome antena parabólica). Como cada raio que incide sobre um objeto de formato parabólico paralelo ao eixo de simetria é refletido diretamente em direção ao foco, ou seja, todos os raios que vão para a antena parabólica estão concentrados no foco e isso pode ser utilizado de diferentes maneiras. É por isso que o foco de uma parábola é tão importante.
Problemas corrigidos com pratos
Exercício 1
Calcule o vértice, o foco e a diretriz da parábola cuja equação é a seguinte:
![]()
Primeiro, a parábola será horizontal porque segue a seguinte expressão da equação reduzida ou canônica da parábola:
![]()
Portanto, seu parâmetro p é:
![]()
![]()
![]()
Por outro lado, como a parábola segue a equação reduzida ou canônica, isso significa que seu vértice ou centro está na origem das coordenadas:
![]()
Depois de conhecermos o vértice e o valor do parâmetro da parábola, podemos calcular facilmente seu foco e diretriz.
O termo quadrático da equação é a variável e ou seja, o eixo da parábola será paralelo ao eixo OX e, de fato, como seu vértice é o ponto (0,0), l O eixo da parábola será o próprio eixo OX. Então, o foco de uma parábola está sempre localizado no eixo da parábola e a uma distância de
![]()
do topo da parábola, cujas coordenadas são:
![]()
![]()
![]()
Da mesma forma, a diretriz está à distância
![]()
do vértice da parábola, que é a origem das coordenadas e é perpendicular ao seu eixo focal. A equação da reta diretora é, portanto:
![]()
![]()
![]()
Exercício 2
Encontre o vértice, o foco e a diretriz da parábola cuja equação é a seguinte:
![]()
A parábola é definida segundo sua equação ordinária (eixo paralelo ao eixo Y), cuja fórmula é:
![]()
Portanto, seu parâmetro p é:
![]()
![]()
![]()
Por outro lado, neste caso a equação ordinária da parábola implica que o seu centro não está na origem das coordenadas, por outro lado, as coordenadas cartesianas do vértice da parábola são os números entre parênteses com o seu sinal alterado :
![]()
Uma vez conhecido o vértice e o valor do parâmetro da parábola, podemos calcular seu foco e diretriz.
O termo quadrático da equação é a variável x de modo que o eixo da parábola seja paralelo ao eixo OY. Assim, o foco de uma parábola está sempre localizado no eixo da parábola e a uma distância de
![]()
do vértice da parábola, de modo que as coordenadas do ponto focal sejam aquelas do vértice, adicionando
![]()
verticalmente:
![]()
![]()
![]()
![]()
Da mesma forma, a diretriz será a linha horizontal localizada a uma distância
![]()
do topo da parábola. A equação da reta diretora é, portanto:
![]()
![]()
![]()
![]()
Exercício 3
Determine a equação parabólica cujo eixo é paralelo ao eixo das abcissas, tem como vértice o ponto V(5,2) e seu foco é o ponto P(8,2).
Neste caso, o vértice da parábola não é a origem das coordenadas, portanto precisamos da equação ordinária para definir a parábola do enunciado. Além disso, o eixo focal da parábola é paralelo ao eixo x, o que significa que a parábola será orientada horizontalmente (os ramos irão para a direita ou para a esquerda) e, portanto, o termo quadrático da equação deve ser a variável você :
![]()
Então podemos substituir as coordenadas do vértice da parábola na equação:
![]()
Agora precisamos encontrar o valor do parâmetro
![]()
A distância da lareira ao topo deve ser
![]()
portanto, podemos encontrar o valor do parâmetro
![]()
da seguinte equação:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} V(5,2) \\[2ex] P(8,2) \end{array} \right\} \longrightarrow \ 8-5 = \cfrac{p}{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91d82e4dce56ca1c48f7c2dba2be5561_l3.png)
![]()
![]()
![]()
![]()
Finalmente, a equação da parábola é:
![]()
![]()
![]()