Nesta página você encontrará o significado da excentricidade da elipse e como ela é calculada (fórmula). Além disso, você verá exemplos de cálculos de excentricidade de elipse.
Qual é a excentricidade da elipse?
A excentricidade da elipse é um parâmetro que mede o quão redonda ou achatada é uma elipse, ou seja, a excentricidade de uma elipse indica o quanto a elipse se assemelha a um círculo.
Por outro lado, lembremos também em que consiste uma elipse: a elipse é o lugar geométrico de todos os pontos de um plano cuja soma das distâncias a dois outros pontos fixos (chamados focos F e F’) é constante.
Fórmula de excentricidade da elipse
Depois de vermos a definição da excentricidade da elipse, vamos ver como ela é calculada a partir de sua fórmula:
A fórmula para a excentricidade da elipse é a seguinte:
![]()
Ouro:
-

é a excentricidade da elipse
-

é a distância de um foco (pontos F e F’) da elipse ao seu centro
-

é o comprimento do semieixo maior (ou maior) da elipse.
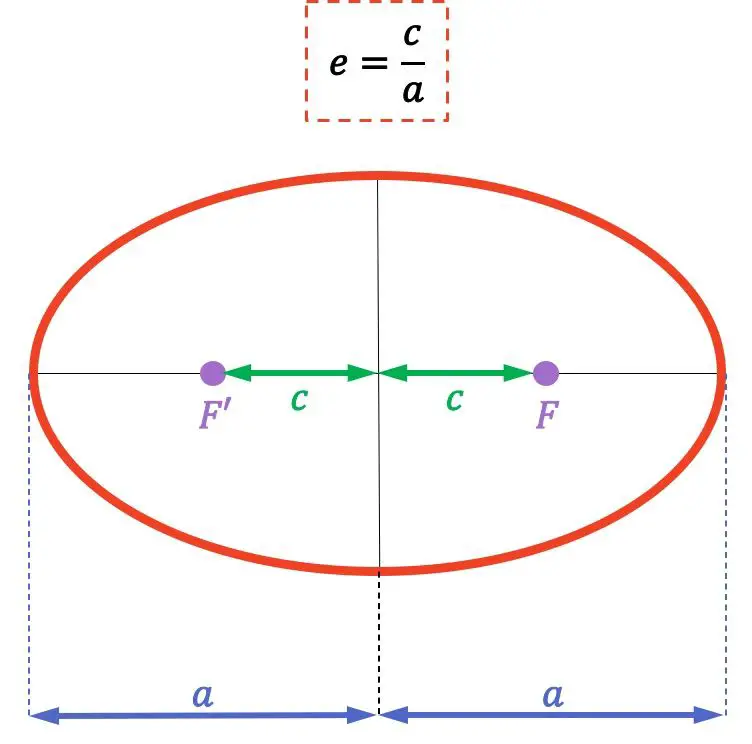
Lembre-se de que os focos de uma elipse são os pontos fixos cuja soma das distâncias a qualquer ponto da elipse é constante. Além disso, a distância entre os dois pontos focais é chamada de distância focal.
O valor da excentricidade varia de zero, o que significa que é um círculo perfeito, a um, o que significa que é uma linha horizontal. Obviamente 0 e 1 não estão incluídos porque os objetos geométricos resultantes não são mais elipses.

![]()
d(P,F)
![]()
d(P,F’)
![]()
tem
![]()
tem

![]()
tem
![]()
contra,
![]()
e= \cfrac{c}{a} = \cfrac{4}{5} = \bm{0,8} $