Aqui você descobrirá como a equação (fórmula) da elipse é calculada, tendo ela a origem como centro ou não. Você também descobrirá quais são os elementos da elipse, como calculá-los e para que servem. Além disso, você poderá ver exemplos e exercícios resolvidos de equações de elipse.
Fórmula da equação da elipse
A fórmula para a equação da elipse em coordenadas cartesianas é:
![]()
Ouro:
-

E

são as coordenadas do centro da elipse:
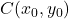
-

é o raio horizontal da elipse.
-

é o raio vertical da elipse.
Equação da elipse centrada na origem
Um tipo de elipse muito comum é aquela cujo centro está na origem das coordenadas, ou seja, no ponto (0,0). É por isso que veremos como determinar a equação da elipse centrada na origem.
Seguindo a fórmula para a equação da elipse:
![]()
Se a elipse estiver centrada na origem das coordenadas, isso significa que
![]()
E
![]()
são iguais a 0, então sua equação será:
![]()
Há matemáticos que também chamam essa expressão de equação canônica ou equação reduzida da elipse.
elementos da elipse
Depois de vermos como é a equação da elipse, veremos quais são seus elementos. Mas primeiro, vamos lembrar o que é exatamente uma elipse:
A elipse é uma linha plana, fechada e curva muito semelhante à circunferência, mas seu formato é mais oval. Em particular, a elipse é o lugar geométrico de todos os pontos de um plano cuja soma das distâncias a dois outros pontos fixos (chamados focos F e F’) é constante.
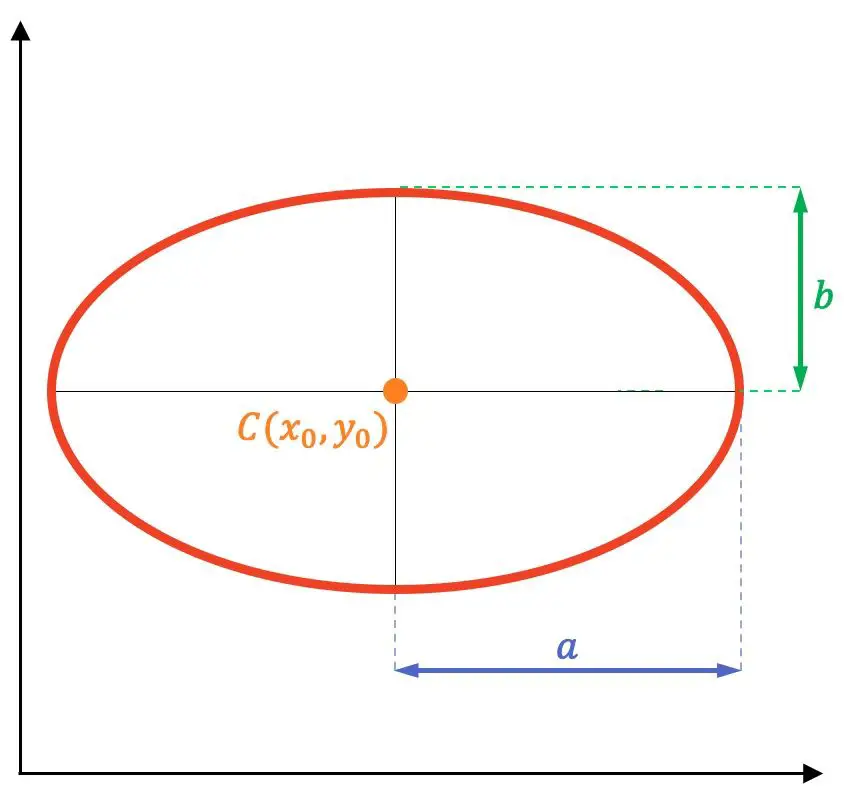
Portanto, os elementos de uma elipse são:
- Os focos : são os pontos fixos F e F’ (pontos de cor roxa na imagem abaixo). A soma das distâncias entre qualquer ponto da elipse e cada foco é constante para todos os pontos da elipse.
- Eixo principal ou focal : é o eixo de simetria da elipse em que se localizam os focais. Também chamado de eixo maior.
- Eixo secundário : é o eixo de simetria da elipse perpendicular ao eixo principal. É também denominado eixo menor e corresponde à bissetriz perpendicular do segmento que une os focos.
- Centro : é o ponto de intersecção dos eixos da elipse. Além disso, é o centro de simetria da elipse (ponto laranja no gráfico).
- Vértices : pontos de intersecção da elipse com seus eixos de simetria (pontos pretos).
- Semieixo maior ou eixo principal: segmento que vai do centro da elipse até os vértices do eixo principal.
- Semi-eixo menor ou eixo secundário: segmento entre o centro da elipse e os vértices do eixo secundário.
- Distância focal : Esta é a distância entre os dois pontos focais.
- Distância semifocal : corresponde à distância entre o centro e cada um dos pontos focais.
- Os vetores de rádio : são os segmentos que unem qualquer ponto da elipse a cada foco (segmentos azuis no gráfico).

Relação entre elementos de uma elipse
Os diferentes elementos de uma elipse estão interligados. Além disso, as relações entre eles são muito importantes para exercícios sobre elipses, pois geralmente são necessárias para resolver problemas sobre elipses e determinar suas equações.
Como vimos acima na definição da elipse, a distância de qualquer ponto da elipse ao foco F mais a distância do mesmo ponto ao foco F’ é constante. Bem, esse valor constante é igual a duas vezes o que o semieixo maior mede. Em outras palavras, a seguinte igualdade é válida para qualquer ponto de uma elipse:
![]()
Ouro
![]()
E
![]()
é a distância do ponto P ao foco F e F’ respectivamente e
![]()
é o comprimento do eixo semifocal.
Portanto, como o vértice do eixo secundário está exatamente no meio do eixo focal, a distância dele a um dos focos é equivalente ao comprimento do eixo semiprimário (
![]()
):
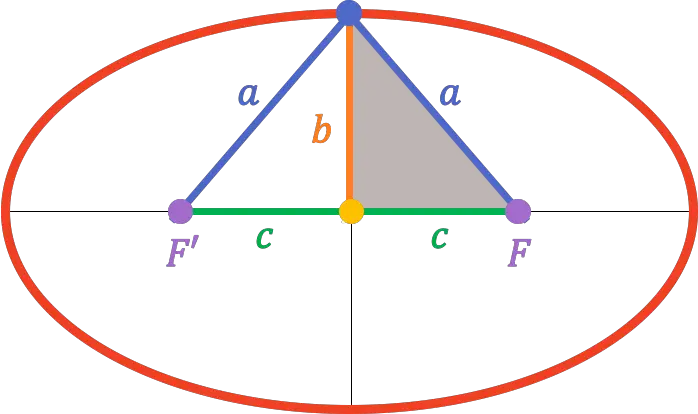
Assim, a partir do teorema de Pitágoras , é possível encontrar a relação que existe entre o semieixo principal, o semieixo secundário e a meia distância focal:
![]()
Lembre-se desta fórmula porque será muito útil para calcular os resultados de exercícios com elipses.
Excentricidade da elipse
Obviamente, nem todas as elipses são iguais, mas algumas são mais alongadas e outras mais achatadas. Portanto, existe um coeficiente que serve para medir o quão arredondada é uma determinada elipse. Este coeficiente é denominado excentricidade e é calculado com a seguinte fórmula:
![]()
Ouro
![]()
é a distância do centro da elipse a um de seus focos e
![]()
o comprimento do semieixo maior.
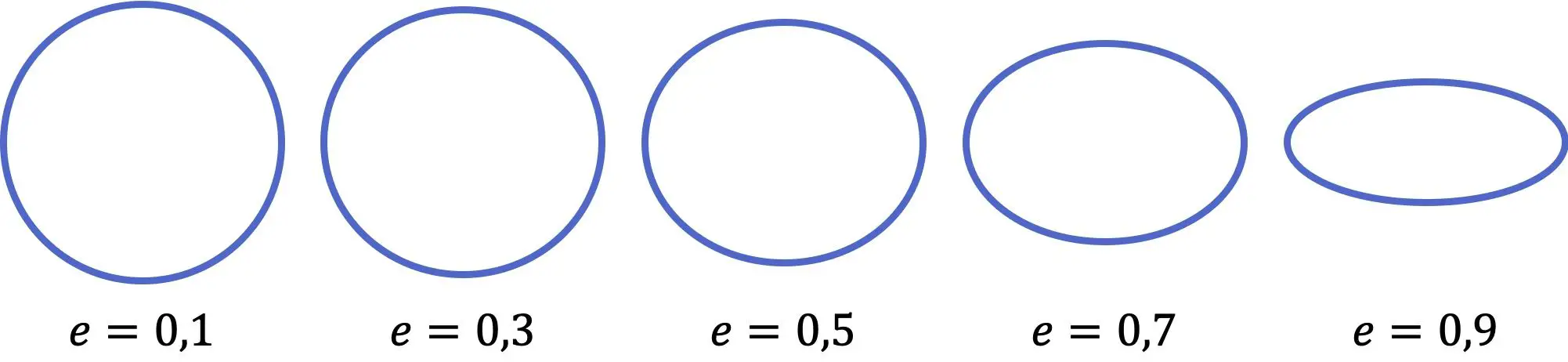
Como você pode ver na representação anterior, quanto menor o valor da excentricidade da elipse, mais ela se assemelha a um círculo, por outro lado, quanto maior o coeficiente, mais achatada é a elipse. Além disso, o valor da excentricidade varia de zero (círculo perfeito) a um (linha horizontal), ambos não inclusivos.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\esquerda(3+\sqrt{24},1}\direita)} \bm{F\esquerda(3-\sqrt{24},1}\direita)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Por fim, se este artigo foi útil para você, certamente também se interessará por nossas páginas sobre a fórmula da hipérbole e a fórmula da parábola . Você encontrará uma explicação detalhada do que são a hipérbole e a parábola, suas equações, suas características, exemplos, exercícios resolvidos,…