Aqui você encontrará tudo sobre retas paralelas: o que significam, como determinar se duas retas são paralelas, suas propriedades, etc. Além disso, você poderá ver diversos exemplos e exercícios resolvidos de retas paralelas.
O que são linhas paralelas?
Linhas paralelas são aquelas que nunca se cruzam, ou seja, mesmo que suas trajetórias se estendam ao infinito, nunca se tocam. Portanto, os pontos de duas retas paralelas estão sempre à mesma distância entre si e, além disso, duas retas paralelas não têm pontos em comum.
Por exemplo, as duas linhas a seguir são paralelas:

Geralmente indicamos que duas linhas são paralelas a 2 barras verticais || entre as linhas
Por outro lado, apesar de duas retas paralelas nunca se cruzarem, em geometria analítica dizemos que formam um ângulo de 0º porque têm a mesma direção.
Quando duas linhas são paralelas?
Depois de vermos a definição de retas paralelas, veremos como determinar duas retas paralelas. Obviamente, uma maneira seria representar graficamente as linhas e ver se elas se cruzam no gráfico, mas existem métodos ainda mais simples e fáceis de usar.
Determine o paralelismo de duas retas com suas inclinações
Você pode saber quando duas retas são paralelas observando a inclinação de cada reta. Lembre-se de que a inclinação de uma linha é o parâmetro
![]()
da equação explícita e da equação ponto-inclinação da reta:
![]()
No entanto, existem várias maneiras de determinar a inclinação de uma reta, portanto, para saber como calculá-la, recomendamos dar uma olhada na fórmula da inclinação de uma reta . Além disso, na página do link você também encontrará uma explicação sobre o que representa a inclinação de uma linha e por que ela é tão importante para uma linha.
Assim, no plano, duas retas são paralelas se tiverem a mesma inclinação (coeficiente m) e ordenadas diferentes na origem (coeficiente n) .
Por exemplo, as duas linhas a seguir são paralelas:
![]()
São duas retas paralelas porque ambas têm a mesma inclinação e, além disso, seus termos independentes são diferentes.
![]()
![]()
Deve-se notar que se duas retas tivessem a mesma inclinação e ao mesmo tempo o mesmo computador na origem, seriam retas idênticas porque seriam exatamente idênticas.
Encontre o paralelismo de duas retas da equação implícita
Lembre-se de que a equação implícita (ou geral) da reta é:
![]()
Assim, se os coeficientes A e B de duas retas são proporcionais entre si, mas não ao coeficiente C , isso significa que as retas são paralelas.
![]()
![]()
Aqui estão duas linhas paralelas expressas em forma de equação geral (ou implícita):
![]()
Eles são paralelos porque os números na frente da variável
![]()
são proporcionais aos números na frente da variável
![]()
, mas não com termos independentes.
![]()
Como antes, se todos os coeficientes (A, B e C) de duas retas implícitas fossem proporcionais, isso implicaria que as duas retas coincidem, ou em outras palavras, que são iguais.
Propriedades de linhas paralelas
As características das linhas paralelas são as seguintes:
- Propriedade simétrica : se uma reta é paralela a outra, esta reta também é paralela à primeira. Esta propriedade também é possuída por linhas perpendiculares.
![]()
- Propriedade transitiva : se uma reta é paralela a outra reta, e esta segunda reta é paralela a uma terceira reta, a primeira reta também é paralela à terceira reta.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8ed30d043440defc6ebfd30c740e937_l3.png)
- O produto escalar dos vetores de direção (vetor que indica a direção de uma reta) de duas retas paralelas é igual ao produto de seus módulos.
![]()
- Além disso, os vetores de direção de duas retas paralelas são sempre linearmente dependentes um do outro, uma vez que são proporcionais .
Esta condição é necessária para que as linhas sejam paralelas, mas não suficiente, ou em outras palavras, duas linhas paralelas devem ter vetores de direção proporcionais, mas o fato de duas linhas terem vetores de direção proporcionais não implica diretamente que sejam paralelas. Já as retas coincidentes também possuem vetores de direção proporcionais.
- As linhas paralelas ao eixo das abcissas (eixo X) são horizontais e sempre têm a forma

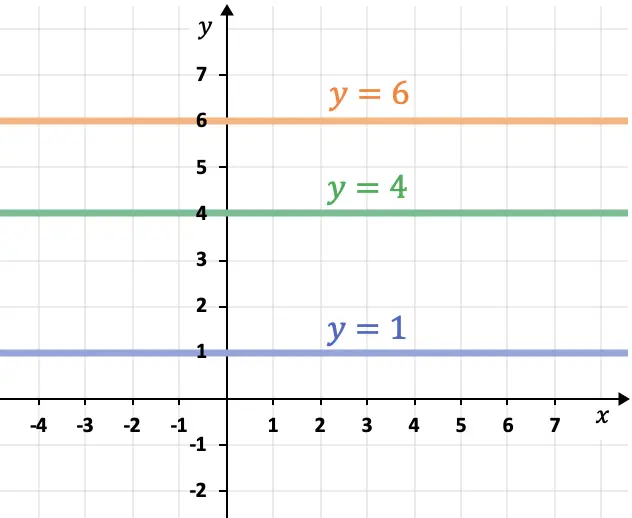
- As linhas paralelas ao eixo do computador (eixo Y) são verticais e sempre seguem a expressão

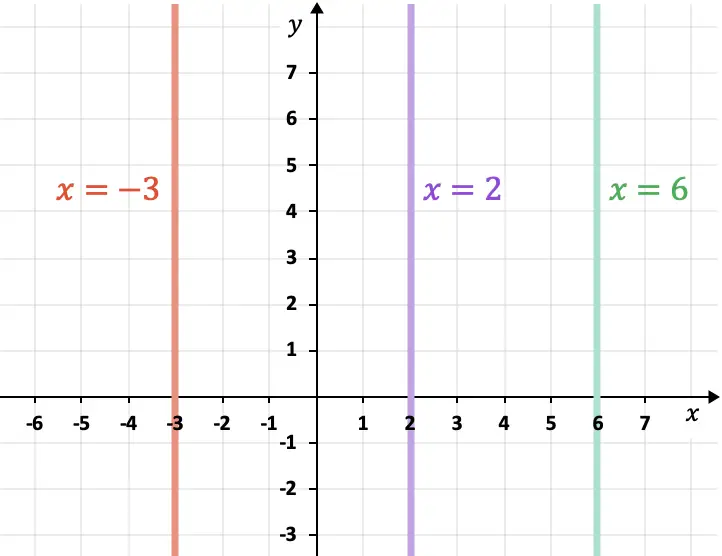
Como calcular a distância entre duas linhas paralelas no plano
Para encontrar a distância entre duas retas paralelas no plano (em R2), basta pegar um ponto em uma das duas retas e calcular a distância deste ponto até a outra reta.
Podemos fazer isso desta forma porque duas retas paralelas estão sempre à mesma distância uma da outra.

Por outro lado, se ao usar a fórmula obtivermos uma distância de 0 unidades, isso significa que as retas se tocam em algum ponto e, portanto, as retas não são paralelas, mas se cruzam, coincidentes ou perpendiculares. Se quiser, você pode conferir as diferenças entre esse tipo de linha em nosso site.
Então, para que você possa ver como isso é feito, determinaremos a distância entre as duas retas paralelas a seguir como exemplo:
![]()
A primeira coisa que precisamos fazer é marcar um ponto em uma das linhas (a que você deseja). Neste caso, calcularemos um ponto na reta
![]()
Para fazer isso, devemos dar um valor a uma das variáveis, faremos por exemplo
![]()
![]()
E agora limpamos a outra variável (
![]()
) da equação obtida para saber quanto vale neste momento:
![]()
![]()
![]()
Portanto, o ponto obtido da reta
![]()
Leste:
![]()
E uma vez que já temos um ponto em uma reta, calculamos a distância desse ponto até a outra reta usando a fórmula da distância de um ponto a uma reta:
![]()
![]()
A distância entre as duas linhas paralelas é, portanto, equivalente a 0,45 unidades .
Linhas paralelas resolveram problemas
Exercício 1
Quais das seguintes linhas são paralelas?
![Rendered by QuickLaTeX.com \begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1baec7cae9d15180df86f9cf4f44d828_l3.png)
Duas retas são paralelas se tiverem a mesma inclinação (e interceptações diferentes). Assim, a inclinação de cada linha é:
![]()
![]()
![]()
![]()
Então apenas as linhas são paralelas
![]()
E
![]()
porque são os únicos que têm inclinações iguais.
Exercício 2
Encontre a equação explícita da reta paralela à reta
![]()
e o que acontece além do ponto
![]()
ser direto
![]()
![]()
Para que a linha seja paralela à linha
![]()
ambos devem ter a mesma inclinação. e a inclinação da linha
![]()
é 3:
![]()
Portanto, a equação explícita da reta que precisamos encontrar será:
![]()
E uma vez que conhecemos a inclinação da reta, podemos calcular a interceptação substituindo o ponto que pertence à reta na equação da reta:
![]()
![]()
![]()
![]()
Portanto, a equação explícita da reta é:
![]()
Exercício 3
Calcule o valor das incógnitas
![]()
E
![]()
de modo que as duas linhas a seguir sejam paralelas:
![]()
As linhas são descritas em forma de equação geral (ou implícita). Portanto, para que as duas retas sejam paralelas, seus coeficientes A e B devem ser proporcionais, ou seja, deve-se cumprir a seguinte equação:
![]()
Devemos, portanto, resolver a equação anterior para obter o valor da incógnita
![]()
Para fazer isso, multiplicamos as frações transversalmente:
![]()
![]()
![]()
Por outro lado, para que as retas sejam paralelas seus termos independentes não podem ser proporcionais aos demais coeficientes:
![]()
Portanto, como antes, resolvemos a desigualdade multiplicando as frações transversalmente:
![]()
![]()
![]()
Em suma, para que as duas linhas sejam paralelas
![]()
deve ser 2 e
![]()
pode ser qualquer número real, exceto 3.
Exercício 4
Qual é a distância entre as duas linhas paralelas a seguir?
![]()
Primeiro, verificaremos se se trata de duas retas paralelas. Para isso, os coeficientes das variáveis
![]()
E
![]()
devem ser proporcionais entre si, mas não aos termos independentes:
![]()
Na verdade, as linhas são paralelas, podemos, portanto, aplicar o procedimento.
Agora precisamos pegar um ponto de uma das retas (a que você deseja). Neste caso, calcularemos um ponto na reta
![]()
Para fazer isso, você deve atribuir um valor a uma das variáveis, por exemplo faremos
![]()
![]()
E agora limpamos a outra variável (
![]()
) da equação obtida para saber seu valor neste ponto:
![]()
![]()
![]()
Para que o ponto obtido da reta
![]()
Leste:
![]()
Depois de conhecermos um ponto em uma reta, calculamos a distância desse ponto até a outra reta com a fórmula:
![]()
![]()