Nesta página você encontrará tudo sobre retas secantes: o que significam, os diferentes tipos que existem, como saber se duas retas são secantes, como encontrar seu ponto comum,… Você também poderá ver vários exemplos e exercícios resolvidos de retas secantes.
O que são duas linhas que se cruzam?
Em matemática, a definição de retas secantes é a seguinte:
Duas linhas se cruzam quando se cruzam em apenas um ponto. Portanto, as linhas que se cruzam têm apenas um ponto em comum. Além disso, duas linhas que se cruzam devem necessariamente estar contidas no mesmo plano cartesiano.
O conceito de que duas retas que se cruzam em um único ponto é importante porque se tivessem mais de um ponto de intersecção seriam retas coincidentes e, por outro lado, se não tivessem ponto de interseção, seriam retas paralelas.
Exemplos de linhas que se cruzam
Depois de vermos o significado de duas linhas que se cruzam, vejamos agora 2 exemplos diferentes deste tipo de linhas:
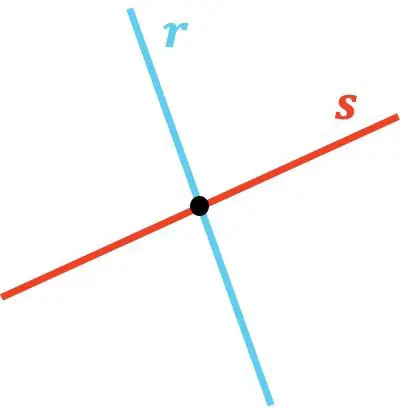
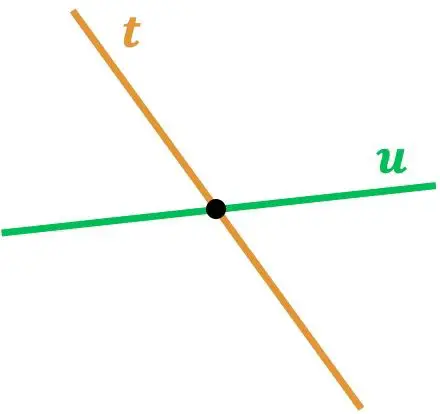
Como você pode ver, as linhas r e s se cruzam porque se tocam em um ponto. E, da mesma forma, a linha t cruza a linha u , pois há um ponto onde elas se cruzam.
Tipos de linhas que se cruzam
Existem dois tipos de linhas que se cruzam:
- Retas perpendiculares : são retas que se cruzam formando um ângulo reto de 90º.
- Linhas oblíquas: consistem em linhas que se cruzam em um ângulo agudo entre 0º e 90º (não incluídas).
Linhas retas perpendiculares

Linhas perpendiculares são aquelas linhas que se cruzam para formar quatro ângulos de 90 graus.
Da mesma forma, as inclinações de duas retas perpendiculares sempre satisfazem a seguinte condição:
![]()
Outra propriedade das linhas perpendiculares que se cruzam é que o produto escalar entre seus vetores de direção (um vetor que indica a direção de uma linha) é igual a zero.
![]()
Se você está mais interessado em retas perpendiculares, neste link você pode ver exemplos de retas perpendiculares . Além disso, você também encontrará como calcular uma reta perpendicular a outra, as propriedades desse tipo de reta, exercícios resolvidos passo a passo, etc.
linhas oblíquas

Linhas oblíquas são aquelas linhas que se cruzam formando ângulos agudos e ângulos obtusos aos pares. Ou seja, faça dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º). Porém, de acordo com a definição do ângulo de duas retas, o ângulo entre duas retas é o menor daqueles que forma.
O ângulo entre duas linhas oblíquas e suas inclinações pode ser calculado usando a seguinte fórmula:
![]()
Como você sabe se duas linhas se cruzam?
Existem basicamente 3 métodos para encontrar a posição relativa de duas linhas:
- Com os vetores de direção das duas retas.
- Com as inclinações das duas linhas.
- Com a equação implícita (ou geral) das duas retas.
A seguir veremos a explicação dos 3 métodos que existem para saber quando duas linhas se cruzam.
Dos vetores de direção das linhas
Se as coordenadas dos vetores de direção (vetor que marca a direção de uma reta) de duas retas diferentes não forem proporcionais , essas duas retas se cruzam.
Vejamos um exercício resolvido passo a passo de duas linhas que se cruzam:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8a2fa136f2840fc1f680e0f7f10ed6_l3.png)
Ambas as linhas são expressas como equações paramétricas, portanto os componentes do vetor de direção de cada linha são os números na frente do parâmetro
![]()
![]()
Então, para ver se os vetores diretores são proporcionais, precisamos dividir as suas coordenadas entre eles. Se obtivermos o mesmo resultado nas duas divisões, elas serão proporcionais; por outro lado, se o resultado for diferente, isso significará que os vetores não são proporcionais.
![]()
As divisões dos componentes não são equivalentes, portanto os vetores não são proporcionais e portanto as retas se cruzam.
no início das encostas
Se duas retas têm inclinações diferentes , isso implica que as retas se cruzam.
Por exemplo, as duas linhas a seguir se cruzam porque têm inclinações diferentes:
![]()
A inclinação da linha
![]()
é -2 e a inclinação da linha
![]()
é 3.
![]()
Como as duas retas não têm a mesma inclinação, elas se cruzam.
Da equação implícita da reta
Também pode ser descoberto se duas retas se cruzam ou não por meio das equações implícitas (ou equações gerais) das retas. A equação implícita da reta é a seguinte:
![]()
Assim, duas retas se cruzam quando seus coeficientes A e B não são proporcionais.
Vejamos um exemplo de duas retas que se cruzam definidas com sua equação implícita:
![]()
Para verificar que se trata de duas retas que se cruzam, devemos analisar a proporcionalidade do coeficiente A (número na frente da variável
![]()
) com o coeficiente B (dígito na frente da variável
![]()
):
![]()
Os dois termos não são proporcionais, portanto as duas linhas se cruzam efetivamente.
Encontre o ponto comum de duas linhas que se cruzam
Como vimos, as retas que se cruzam têm apenas um ponto em comum. Assim, para calcular o ponto de intersecção de duas retas secantes , é necessário resolver o sistema de equações formado pelas duas retas.
Como exemplo, encontraremos o ponto de intersecção das duas retas a seguir:
![]()
Para determinar o ponto de intersecção das duas retas, devemos resolver o sistema de equações lineares formado pelas duas retas:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77ae257986963d3652d5996fc09be9fb_l3.png)
Neste caso, resolveremos o sistema com o método de substituição. Iremos, portanto, isolar a variável
![]()
da primeira equação e substitua-a na segunda equação:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3ad955c3f2ebeb8ad0bdee85a226c73b_l3.png)
![]()
![]()
![]()
![]()
![]()
E quando soubermos quanto vale o desconhecido
![]()
Substituímos seu valor na expressão encontrada para
![]()
![]()
![]()
A solução do sistema de equações é, portanto, o ponto de intersecção das duas retas. E este ponto é
![]()
linha que cruza um círculo
Normalmente, quando dizemos que duas retas se cruzam, estamos nos referindo ao conceito que acabamos de ver. Porém, em geometria, há outro significado da reta secante:
Uma linha que cruza um círculo é uma linha que cruza um círculo (ou uma curva) em dois pontos diferentes.
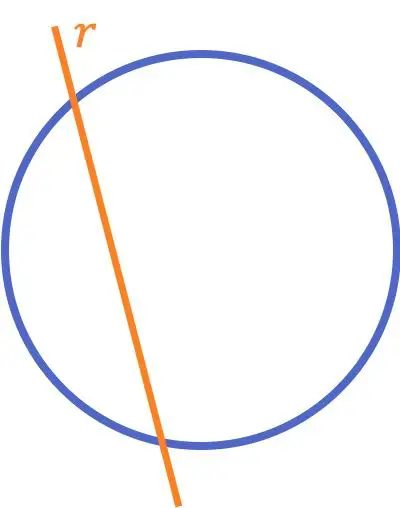
Ao contrário do conceito de duas linhas que se cruzam, normalmente ensinado na escola primária, esta definição de uma linha que se cruza com um círculo é frequentemente estudada em aulas posteriores, juntamente com todas as posições relativas de linhas com círculos.