Nesta página você encontrará a explicação dos diferentes métodos que existem para determinar a posição relativa de duas retas no plano (em R2). Além disso, você verá vários exemplos e poderá praticar com exercícios resolvidos passo a passo.
Qual é a posição relativa de duas retas no plano?
Antes de olhar para as posições relativas entre duas retas no plano, obviamente você precisa saber exatamente o que é uma reta, você pode encontrá-la na definição de reta .
Assim, ao trabalhar em duas dimensões (em R2), existem 3 tipos de posições relativas possíveis entre duas linhas:
linhas que se cruzam

Duas linhas que se cruzam têm apenas um ponto em comum.
Linhas paralelas

Duas retas são paralelas se não têm ponto comum. Isto é, se eles nunca se cruzarem.
linhas coincidentes

Duas retas são iguais se todos os seus pontos forem comuns.
Por outro lado, o ângulo entre duas linhas no plano também depende da sua posição relativa:
- As linhas que se cruzam se cruzam em um ângulo entre 0º (não incluído) e 90º (inclusive). Além disso, se formarem apenas um ângulo reto de 90º, isso significa que as duas linhas são perpendiculares.
- Retas paralelas formam um ângulo de 0º, pois possuem a mesma direção.
- E, pelo mesmo motivo, as retas coincidentes também fazem um ângulo de 0º entre elas.
Se você quiser saber como o ângulo entre duas linhas é calculado, você pode verificar a fórmula do ângulo entre duas linhas . Aqui você encontrará uma explicação detalhada de como determinar o ângulo entre duas retas, além de diversos exemplos e até exercícios resolvidos para que você possa praticar e compreender totalmente o conceito.
Como encontrar a posição relativa de duas retas no plano
Conhecer a posição relativa entre duas linhas no espaço bidimensional depende de como as linhas são expressas:
- Vetores de direção de linha: se duas linhas tiverem um vetor de direção diferente, elas deverão se cruzar. Por outro lado, se as coordenadas dos seus vetores de direção forem iguais ou proporcionais, podem ser paralelos ou coincidentes (é necessário verificar se possuem um ponto comum).
- Equação explícita: quando duas retas têm inclinações diferentes
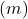
eles secam Pelo contrário, se as linhas têm a mesma inclinação, mas uma ordem diferente na origem
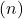
eles são paralelos. Finalmente, duas retas são confundidas quando originalmente têm inclinações e ordenadas iguais.
- Equação geral (ou implícita): duas retas com coeficientes não proporcionais A e B sempre se cruzarão. Porém, serão paralelos quando estes dois parâmetros forem proporcionais entre si, mas não ao coeficiente C. E, finalmente, quando os três termos forem proporcionais, isso implica que as retas estão confusas.
Se você tiver alguma dúvida sobre as equações da reta acima, pode consultar a explicação das equações da reta no plano . Aqui você encontrará a fórmula de todas as equações lineares, como são calculadas, exemplos e exercícios resolvidos de equações lineares.
Na tabela a seguir você tem um resumo das propriedades anteriores:

A seguir, veremos dois exemplos de como determinar a posição relativa entre duas linhas:
Exemplo 1
- Encontre a posição relativa entre as duas linhas a seguir definidas na forma de uma equação explícita:
![]()
As duas linhas têm a mesma inclinação:
![]()
Mas eles têm computadores diferentes na origem:
![]()
Portanto, como têm a mesma inclinação, mas interceptações diferentes, as retas são paralelas .
Exemplo 2
- Determine a posição relativa entre as duas linhas a seguir expressas com sua equação implícita (ou geral):
![]()
Ambas as retas são expressas como uma equação explícita, portanto precisamos ver se algum de seus coeficientes é proporcional:
![]()
Os 3 termos das retas são proporcionais, portanto as retas coincidem .
Determine a posição relativa de duas retas no plano com um sistema de equações
Outra forma de saber a posição relativa entre duas retas é analisar o sistema de equações formado pelas equações das retas:
- Se o sistema tiver uma solução única , as linhas se cruzam. Além disso, o ponto de intersecção das duas retas é a solução do sistema.
- Se for um sistema sem solução , isso indica que as retas não possuem pontos em comum e, portanto, são retas paralelas.
- Se o sistema tiver infinitas soluções , isso significa que as retas possuem todos os pontos em comum e, portanto, são retas que se cruzam.
Exemplo 3
- Calcule a posição relativa das duas linhas a seguir usando um sistema de equações:
![]()
Para encontrar a posição relativa das duas retas, precisamos resolver o seguinte sistema de equações lineares formado pelas duas retas:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-243b1e787e6532fbafbfca53d934f4ad_l3.png)
Neste caso, resolveremos o sistema com o método de substituição. Iremos, portanto, isolar a variável
![]()
da segunda equação e substitua-a na primeira equação:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad3456c92c838f40d60afdb45e1eb2f3_l3.png)
![]()
![]()
![]()
![]()
![]()
E quando soubermos quanto vale o desconhecido
![]()
Substituímos seu valor na expressão encontrada para
![]()
![]()
![]()
Obtivemos, portanto, apenas uma solução do sistema de equações composto pelas duas retas, portanto as duas retas se cruzam . E o ponto onde eles se cruzam é a solução do sistema, ou seja, o ponto
![]()
Problemas resolvidos de posição relativa de duas retas no plano
Exercício 1
Determine se as seguintes linhas se cruzam, são paralelas ou coincidem:
![]()
Ambas as retas são expressas como uma equação implícita (ou geral), portanto precisamos ver se algum de seus coeficientes é proporcional:
![]()
Apenas os coeficientes A e B das retas são proporcionais entre si, e não ao coeficiente C. Portanto as duas retas são paralelas .
Exercício 2
Encontre a posição relativa entre as duas linhas a seguir expressas como equações paramétricas:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bafb951a2141722b0bbb7a1681f506ea_l3.png)
Poderíamos resolver o sistema de equações formado pelas duas retas para encontrar sua posição relativa. Porém, por estarem na forma de equações paramétricas, pode-se facilmente encontrar seus vetores de direção e se não forem proporcionais significa que as retas se cruzam. E neste caso, não gastaremos tanto tempo resolvendo todo um sistema de equações.
Para que as coordenadas cartesianas do vetor de direção de cada linha sejam os números na frente do parâmetro
![]()
![]()
Uma vez conhecidos os vetores de direção, verificamos sua proporcionalidade:
![]()
Os vetores de direção não são proporcionais, portanto as linhas se cruzam .
Exercício 3
Indique se as seguintes linhas se cruzam, são paralelas ou coincidentes e também encontre um ponto de intersecção entre elas (se aplicável).
![]()
As duas retas são definidas por sua equação explícita e têm inclinações diferentes:
![]()
Como possuem inclinações diferentes, as linhas se cruzam .
Portanto, como as retas se cruzam, elas terão 1 ponto em comum e para calculá-lo devemos resolver o sistema de equações formado pelas duas retas:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3923ff74a214543ddd2cc44a42e3813_l3.png)
Neste caso resolveremos o sistema com o método de equalização porque ambos
![]()
já foram excluídos:
![]()
![]()
![]()
![]()
![]()
E uma vez que temos o desconhecido
![]()
substituímos seu valor em qualquer expressão de
![]()
para saber quanto vale:
![]()
![]()
Portanto, o ponto de intersecção das duas retas é o resultado do sistema:
![]()
Exercício 4
Calcule o valor das incógnitas
![]()
E
![]()
de modo que as duas linhas a seguir sejam paralelas:
![]()
As linhas são descritas em forma de equação geral (ou implícita). Portanto, para que as duas retas sejam paralelas, seus coeficientes A e B devem ser proporcionais, ou seja, deve-se cumprir a seguinte equação:
![]()
Devemos, portanto, resolver a equação anterior para obter o valor da incógnita
![]()
Para fazer isso, multiplicamos as frações transversalmente:
![]()
![]()
![]()
Por outro lado, para que as retas sejam paralelas seus termos independentes não podem ser proporcionais aos demais coeficientes:
![]()
Portanto, como antes, resolvemos a desigualdade multiplicando as frações transversalmente:
![]()
![]()
![]()
Em suma, para que as duas linhas sejam paralelas
![]()
deve ser 2 e
![]()
pode ser qualquer número real, exceto 3.
Exercício 5
Encontre a equação explícita da reta paralela à reta
![]()
e o que acontece além do ponto
![]()
ser direto
![]()
![]()
Para que a linha seja paralela à linha
![]()
ambos devem ter a mesma inclinação. e a inclinação da linha
![]()
é 2:
![]()
Portanto, a equação da reta que precisamos encontrar será:
![]()
E uma vez que conhecemos a inclinação da reta, podemos calcular a interceptação y substituindo o ponto que pertence à reta na equação da reta:
![]()
![]()
![]()
![]()
![]()
Portanto, a equação explícita da reta é:
![]()
Se você chegou até aqui, significa que já dominou as posições relativas entre duas linhas no plano. Bom trabalho!
Mas uma coisa que muitos se perguntam é… e qual é a utilidade de saber a posição relativa entre duas linhas?
Pois bem, uma das aplicações da posição relativa entre linhas é poder saber a distância entre 2 linhas, já que o cálculo da distância entre duas linhas depende da sua posição relativa:
- Se as linhas se cruzarem ou coincidirem, a distância será zero.
- Por outro lado, quando as retas são paralelas, deve ser aplicada uma fórmula específica. Se você estiver mais interessado, pode conferir como é calculada a distância entre duas retas paralelas .