Nesta página você verá a explicação da magnitude de um vetor e como calculá-lo com sua fórmula. Você também poderá ver como encontrar o módulo a partir de dois pontos: sua origem e seu fim. Além disso, você descobrirá como determinar os componentes de um vetor a partir de seu módulo e das propriedades do módulo de um vetor. Você pode até praticar com exemplos, exercícios e problemas passo a passo.
Qual é o módulo de um vetor?
A magnitude de um vetor representa a distância entre sua origem e seu fim. Portanto, a magnitude de um vetor é igual ao comprimento desse vetor.
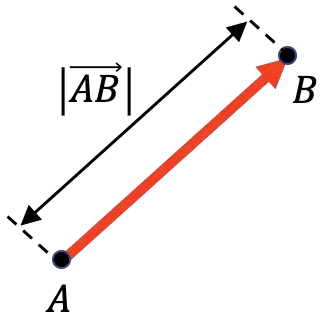
Como você pode ver na representação gráfica acima, a magnitude de um vetor é simbolizada por uma barra vertical em cada lado do vetor:
![]()
Por outro lado, o módulo de um vetor é igual à norma de um vetor , então você também pode vê-lo escrito dessa forma. É por isso que existem matemáticos que também representam o módulo de um vetor com duas barras verticais de cada lado:
![]()
Fórmula para o módulo de um vetor
Para encontrar a magnitude de um vetor no plano, devemos aplicar a seguinte fórmula:
Para determinar a magnitude de um vetor, devemos calcular a raiz quadrada (positiva) da soma dos quadrados de seus componentes. Em outras palavras, se tivermos o seguinte vetor:
![]()
Seu módulo é:
![]()
Por exemplo, calcularemos a magnitude do seguinte vetor usando a fórmula:
![]()
![]()
Calcule a magnitude de um vetor com as coordenadas de sua origem e fim
Acabamos de ver como a magnitude de um vetor é determinada quando conhecemos suas componentes, mas o que aconteceria se soubéssemos apenas os pontos onde ele começa e onde termina?
Assim, para calcular a magnitude de um vetor a partir das coordenadas de sua origem e de seu final, você deve seguir estes dois passos:
- Primeiro encontramos os componentes do vetor. Para fazer isso, precisamos subtrair o extremo menos a origem.
- E a seguir calculamos o módulo do vetor obtido com a fórmula que vimos na seção anterior.
Vamos ver como isso é feito através de um exemplo:
- Calcule a magnitude do vetor cuja origem é o ponto
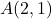
e como ponto final
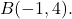
Primeiro precisamos encontrar as componentes do vetor, então subtraímos seu ponto final menos sua origem:
![]()
Uma vez conhecido o vetor, calculamos sua magnitude usando a fórmula de magnitude vetorial:
![]()
E deixamos o resultado como raiz quadrada, porque não é exato.
Como calcular as componentes de um vetor a partir do seu módulo
Vimos como extrair a norma de um vetor a partir das suas componentes, mas o processo também pode ser invertido. Em outras palavras, podemos calcular as componentes de um vetor através do seu módulo.
O processo de encontrar os componentes de um vetor a partir de sua magnitude é chamado de decomposição vetorial . Então, para decompor um vetor, precisamos do seu módulo, obviamente, e do ângulo que ele forma com o eixo das abcissas (eixo X).
Para que os componentes X e Y do vetor possam ser calculados com as razões trigonométricas:

Como você pode ver na imagem, a magnitude de um vetor forma um triângulo retângulo com seus componentes, portanto as fórmulas elementares da trigonometria podem ser aplicadas.
Deve-se levar em conta que, diferentemente do módulo de um vetor, suas componentes podem ser negativas porque o seno e o cosseno podem assumir valores negativos.
Como exemplo, resolveremos a decomposição vetorial do vetor cuja magnitude e ângulo com o eixo OX são:
![]()
A componente horizontal do vetor é igual ao módulo multiplicado pelo cosseno do ângulo:
![]()
E a componente vertical do vetor é igual a multiplicar o módulo pelo seno do ângulo:
![]()
Então o vetor é o seguinte:
![]()
Propriedades de módulo de um vetor
Módulo é um tipo de operação vetorial que possui as seguintes características:
- A magnitude de um vetor nunca pode ser negativa , será sempre igual ou maior que 0.
![]()
Na verdade, o único vetor que existe com magnitude zero é o vetor zero, ou seja, o vetor
![]()
- A magnitude do produto de um vetor por um número real (ou escalar) é equivalente a multiplicar o valor absoluto do escalar pela magnitude do vetor. Portanto, vale a seguinte igualdade:
![]()
- A desigualdade triangular é verificada: o módulo da soma de dois vetores é menor ou igual à soma de seus módulos separadamente.
![]()
- Além disso, a magnitude da soma de dois vetores está relacionada ao produto escalar pela seguinte equação:
![]()
vetor unitário
Em matemática, um vetor unitário é um vetor cujo módulo é igual a um.
![]()
Portanto, o comprimento de um vetor unitário é uma unidade.
Pode parecer muito difícil para um vetor ter um módulo exatamente 1, mas na verdade é fácil encontrar este tipo de vetor:
Para encontrar o vetor unitário de qualquer vetor, basta dividi-lo pelo seu módulo:
![]()
Ouro
![]()
é o vetor unitário de
![]()
E
![]()
seu módulo.
O vetor unitário também é chamado de versor ou vetor normalizado.
Além disso, o vetor unitário tem a mesma direção e sentido do vetor original.
Por exemplo, calcularemos o vetor unitário do seguinte vetor:
![]()
Para normalizar o vetor, primeiro precisamos calcular sua magnitude:
![]()
E, por fim, calculamos o vetor unitário dividindo o vetor original pelo seu módulo:
![]()
Exercícios de módulo vetorial resolvidos
Exercício 1
Calcule a magnitude do seguinte vetor:
![]()
Para calcular o módulo do vetor devemos aplicar sua fórmula:
![]()
Exercício 2
Ordene os seguintes vetores do mais curto para o mais longo.
![]()
![]()
![]()
![]()
O comprimento de um vetor é igual à sua magnitude. Portanto, precisamos calcular os módulos de todos os vetores:
![]()
![]()
![]()
![]()
Assim, os vetores ordenados do menor para o maior comprimento (ou módulo) são:
![]()
Exercício 3
Determine a magnitude do vetor cuja origem é o ponto
![]()
e como ponto final
![]()
Para calcular seu módulo, primeiro você deve encontrar o vetor. Para fazer isso, subtraímos o extremo menos a origem:
![]()
Uma vez conhecido o vetor, seu módulo é calculado usando a fórmula do módulo:
![]()
Exercício 4
Decomponha o seguinte vetor e encontre seus componentes:
![]()
A componente horizontal do vetor é igual ao módulo multiplicado pelo cosseno do ângulo:
![]()
E a componente vertical do vetor é igual a multiplicar o módulo pelo seno do ângulo:
![]()
Então o vetor é o seguinte:
![]()
Neste caso, as duas componentes são idênticas, ou seja, o ângulo de inclinação do vetor é de 45º.
Exercício 5
Calcule o vetor com a mesma direção e sentido do vetor a seguir, mas com módulo 1.
![]()
O vetor com a mesma direção e mesmo sentido, mas com módulo 1, é o vetor unitário. Para calculá-lo, primeiro encontramos o módulo do vetor:
![]()
E agora calculamos o vetor unitário dividindo o vetor original pelo seu módulo:
![]()
Exercício 6
Decomponha vetorialmente o seguinte vetor e calcule seu vetor unitário:
![]()
Primeiro, decompomos o vetor e encontramos suas coordenadas:
![]()
![]()
Então o vetor é o seguinte:
![]()
E agora calculamos o vetor unitário dividindo o vetor obtido pelo seu módulo:
![]()
Observe que os componentes de um vetor unitário são iguais ao cosseno e ao seno do ângulo que ele forma com o eixo X.