Esta página explica como multiplicar um vetor por um número real (ou escalar) numericamente e graficamente. Além disso, você também encontrará exemplos e exercícios resolvidos do produto de um vetor por um escalar. Por fim, também são explicadas as propriedades deste tipo de operação com vetores.
Como você multiplica um vetor por um número real?
Para calcular numericamente o produto de um vetor e um número (ou escalar), cada componente do vetor deve ser multiplicado pelo número.
![]()
![]()
Assim, o resultado da multiplicação de um vetor por um número dá origem a um novo vetor com as seguintes características:
- O resultado do produto de um vetor por um escalar produz um novo vetor com a mesma direção do vetor original.
- Além disso, o novo vetor terá a mesma direção se o número for positivo.
- Ou terá o significado oposto se o número for negativo.
- A magnitude do vetor resultante é equivalente à magnitude do vetor original vezes o escalar.
No gráfico a seguir você pode ver como a direção do vetor é mantida independentemente do sinal do escalar. Por outro lado, a direção do vetor depende do sinal do número que ele multiplica.

Além disso, no gráfico a seguir vê-se claramente que a magnitude do vetor produto resultante é igual à magnitude do vetor original multiplicado pelo escalar.
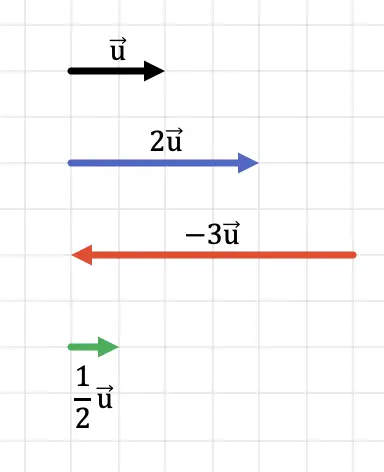
Obviamente, se multiplicarmos o vetor por um número maior que 1, o resultado será um vetor de maior comprimento (de maior módulo). Por outro lado, se multiplicarmos o vetor por um número menor que 1, o resultado será um vetor de comprimento menor (módulo menor).
Nota: Não confunda o produto de um vetor e um escalar com o produto escalar de vetores . Embora tenham um nome semelhante, são dois conceitos completamente diferentes.
Exemplo de produto de um vetor por um escalar
A seguir, veremos um exemplo numérico de como é calculado o produto de um vetor e um número:
- Multiplique o seguinte vetor por 4:
![]()
![]()
Como você viu, esse tipo de operação vetorial não é muito complicada, pois não é necessário fazer muitos cálculos.
No entanto, existem operações vetoriais mais complicadas, como adição e subtração de vetores. Se você já entendeu como calcular o produto de um vetor e um escalar, recomendamos que passe para o próximo nível e veja como resolver adição e subtração vetorial, pois são operações um pouco mais difíceis e, na verdade, eles são muito mais usados (são mais importantes).
Propriedades de multiplicar um vetor por um número
O produto de um vetor por um número possui as seguintes propriedades:
- Propriedade associativa : Quando o vetor é multiplicado por mais de um número, a ordem das multiplicações não importa.
![]()
- Propriedade distributiva em relação à adição e subtração de vetores:
![]()
![]()
- Propriedade distributiva em relação à adição de escalares:
![]()
- Elemento neutro : Obviamente, qualquer vetor multiplicado por 1 dá o próprio vetor:
![]()
Problemas resolvidos de multiplicação de um vetor por um escalar
Exercício 1
Calcule analiticamente o resultado do produto do seguinte vetor por 3:
![]()
Para encontrar o produto, você deve multiplicar cada coordenada do vetor por 3:
![]()
Exercício 2
Multiplique o seguinte vetor por 6 e encontre seu módulo:
![]()
Primeiro multiplicamos o vetor pelo escalar:
![]()
Existem agora duas maneiras de calcular a magnitude do vetor obtido. A primeira é encontrar a magnitude do vetor original e depois multiplicá-la por 6:
![]()
![]()
E a segunda forma é calcular diretamente a magnitude do vetor obtido na multiplicação:
![]()
Assim, com ambos os procedimentos mostra-se que o resultado não depende do método pelo qual o módulo é calculado.
Exercício 3
Do seguinte vetor:
![]()
Calcule as seguintes operações algebricamente:
![]()
![]()
![]()
![]()
A seguir, determine se os vetores resultantes têm a mesma direção e sentido do vetor original e ordene-os do mais curto para o mais longo.
Primeiro calculamos as multiplicações:
![]()
![]()
![]()
![]()
Portanto, os vetores multiplicados por números positivos têm a mesma direção e sentido do vetor original. E os vetores multiplicados por números negativos têm a mesma direção, mas a direção oposta ao vetor original.
Vetores da mesma direção e da mesma direção:
![]()
E
![]()
Vetores com a mesma direção, mas com significados diferentes:
![]()
Finalmente, devemos ordenar os vetores de acordo com o seu comprimento, ou equivalentemente, o seu módulo. O vetor de maior comprimento (ou maior módulo) será aquele que foi multiplicado por um número maior (em valor absoluto), e o vetor de menor comprimento (ou menor módulo) será aquele que foi multiplicado por um menor número (em valor absoluto). Então a ordem dos comprimentos é:
![]()
Observe que o comprimento ou módulo não depende do sinal do escalar que é multiplicado, pois a direção do vetor não modifica seu módulo.
Exercício 4
Considere os dois vetores a seguir:
![]()
Calcule a seguinte operação:
![]()
Primeiro resolvemos as multiplicações de vetores por números:
![]()
![]()
![]()
E então subtraímos os vetores:
![]()
![]()
Exercício 5
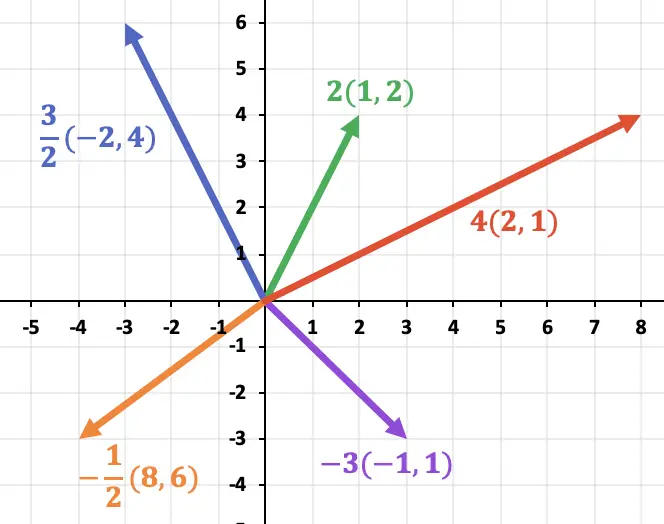
Execute as seguintes multiplicações de vetores por escalares e represente graficamente os resultados:
![]()
![]()
![]()
![]()
![]()
Primeiro multiplicamos os vetores pelos escalares reais:
![]()
![]()
![]()
![]()
![]()
Finalmente, uma vez calculados os vetores, nós os representamos no gráfico: