Esta página explica como adicionar dois vetores no plano, gráfica e numericamente. Existem 3 maneiras de adicioná-los graficamente: o método do paralelogramo, cabeça com cauda e polígono. Além disso, você também encontrará exercícios resolvidos sobre adição de vetores e todas as propriedades da adição de vetores.
Como adicionar dois vetores graficamente?
Basicamente, existem duas maneiras de adicionar vetores a partir de sua representação gráfica. Com ambas as formas obtém-se o mesmo resultado, mas alguns preferem adicioná-las usando o método cabeça-cauda e outros com o método do paralelogramo . Portanto, explicaremos os dois métodos para que você escolha o que preferir. 😉
Por outro lado, estes dois métodos são usados para somar dois vetores, mas o que acontece se quisermos somar mais de dois vetores? É portanto necessário utilizar o método do polígono , que consiste em utilizar sucessivamente o método do paralelogramo. Você também encontrará sua explicação após os métodos cabeça-cauda e paralelogramo.
Método ou regra do paralelogramo
A regra do paralelogramo ou método do paralelogramo (ou lei do paralelogramo) é um procedimento gráfico que permite encontrar a soma de dois vetores de uma forma muito simples. As etapas a seguir para aplicar este processo são as seguintes:
- Primeiramente traçamos os vetores e os posicionamos no mesmo ponto de aplicação, ou seja, colocamos as origens de ambos os vetores no mesmo ponto.
- Então desenhamos no final de um vetor uma linha paralela ao outro vetor. E repetimos o passo com o outro vetor. Obteremos, portanto, o desenho de um paralelogramo (daí o nome da regra).
- Por fim, o resultado da soma será o vetor que vai da origem comum até o ponto onde as duas retas paralelas se cruzam.
Veja o seguinte exemplo genérico em que dois vetores são adicionados com a regra do paralelogramo:

O resultado da soma dos vetores é a diagonal do paralelogramo que eles formam com seus paralelos.
método cabeça e cauda
O método head and tail , ou também conhecido como método do triângulo , é outro procedimento com o qual dois vetores podem ser adicionados graficamente. Neste caso, os passos a seguir são:
- Mova um vetor adicionado e coloque-o de forma que sua origem fique logo no final do outro vetor adicionado.
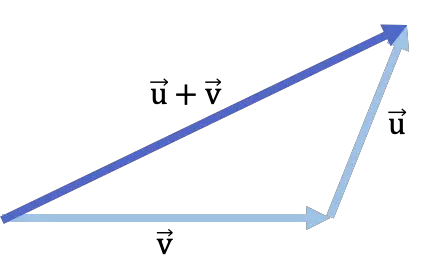
- O resultado da adição de vetores é o segmento que vai do início do primeiro vetor adicionado até o final do outro vetor. Se você olhar de perto, um triângulo é concluído com os dois vetores adicionados e o vetor adicionado.
Aqui está um exemplo de adição de vetores usando o método head-to-tail:
método polígono
Depois de vermos como resolver graficamente a soma de dois vetores, veremos como isso é feito quando temos mais de dois vetores.
Quando se deseja somar três ou mais vetores, existe uma técnica para agilizar o cálculo da operação. Esta técnica é chamada de método do polígono e consiste na aplicação sucessiva do método cabeça-cauda:
- Primeiro precisamos colocar cada vetor após o outro, de modo que a origem de um vetor coincida com o fim de outro vetor. A ordem em que os colocamos é irrelevante.
- E o resultado da soma é o vetor obtido unindo o início do primeiro vetor ao final do último vetor.
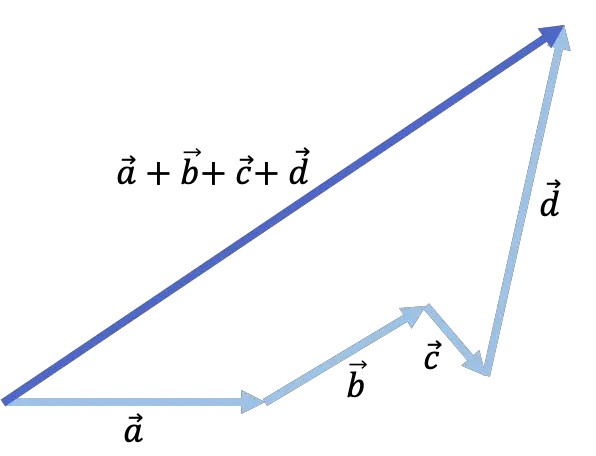
Veja o exemplo a seguir onde 4 vetores são adicionados:
Calcule a soma de dois vetores numericamente
Assim que soubermos como adicionar vetores geometricamente, veremos como calcular uma soma vetorial numericamente ou algebricamente.
Para somar numericamente dois vetores, você deve somar seus respectivos componentes. Ou, em outras palavras, as coordenadas X dos dois vetores são somadas entre si e iguais às coordenadas Y.
![]()
![]()
Por exemplo, a soma entre vetores
![]()
E
![]()
Leste:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(1,2) +(5, 3) \\[2ex] & = (1+5,2+3) \\[2ex] & = \bm{(6,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c0813ac0f7ad7fafa1f20b6284430a5_l3.png)
Por outro lado, devemos ter em mente que a adição vetorial de dois vetores não é a mesma que a adição dos módulos dos vetores, na verdade os resultados são totalmente diferentes. Você pode ver as diferenças entre as duas operações nas propriedades da magnitude vetorial (também chamada de magnitude vetorial).
Adicionar propriedades de vetor
A adição de vetores tem as seguintes características:
- Propriedade associativa : Colocar parênteses entre a soma de vários vetores não modifica o resultado da operação.
![]()
- Propriedade Comutativa – Ao contrário da subtração vetorial, o resultado da adição entre dois vetores é independente da ordem em que são adicionados.
![]()
- Propriedade do elemento oposto : a soma de um vetor mais seu oposto, ou seja, sua negação, é igual a 0.
![]()
- Propriedade do elemento neutro : obviamente, qualquer vetor mais o vetor nulo ou nulo é equivalente ao próprio vetor:
![]()
Problemas resolvidos de adição de vetores
Exercício 1
Calcule a soma dos vetores graficamente
![]()
E
![]()
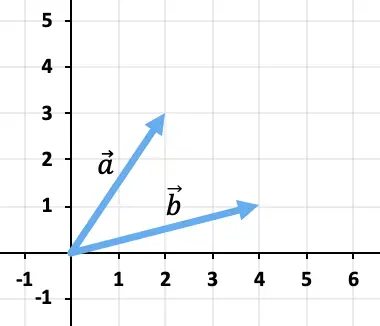
Para adicionar os dois vetores, usaremos a regra da cabeça e da cauda. Portanto, colocaremos a origem do vetor
![]()
no final do vetor
![]()
, e a soma será o vetor que vai da origem das coordenadas até o final de
![]()
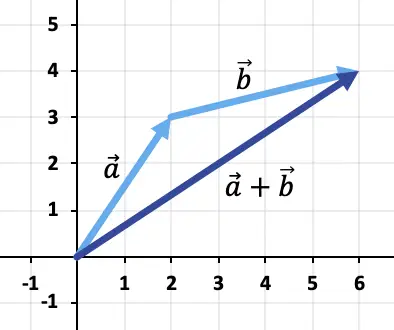
Portanto, o resultado da adição de vetores é:
Exercício 2
Resolva a soma dos vetores graficamente
![]()
E
![]()
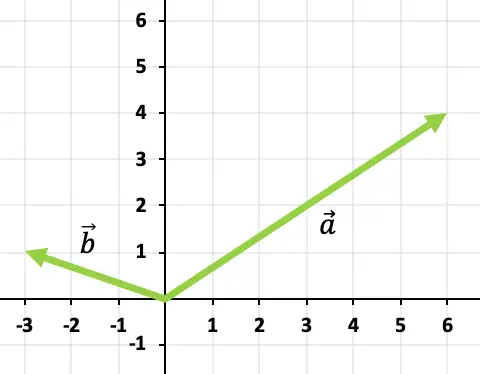
Para adicionar os dois vetores, usaremos a regra cabeça-cauda. Vamos, portanto, localizar a origem do vetor
![]()
no final do vetor
![]()
, e o vetor soma será aquele que vai da origem dos eixos até o final de
![]()
Portanto, o resultado da adição de vetores é:
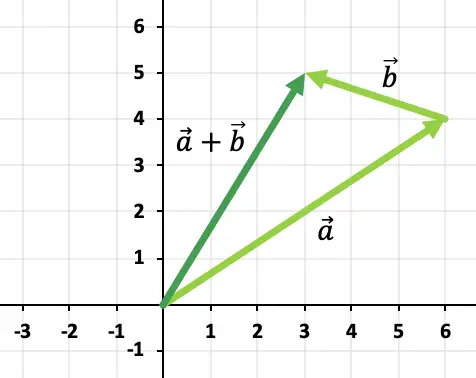
Exercício 3
Determine graficamente o vetor resultante da soma de todos os vetores representados no gráfico:
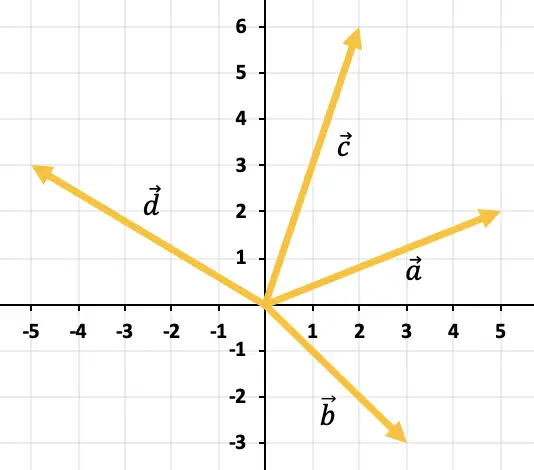
Para adicionar mais de 2 vetores do gráfico, você deve usar a regra do polígono. Devemos, portanto, mover os vetores para que permaneçam contínuos, ou seja, um após o outro (a ordem é irrelevante). Portanto a soma de todos os vetores será o vetor que vai da origem do primeiro vetor até o final do último vetor.
Portanto o resultado da soma dos 4 vetores é o vetor representado em vermelho:
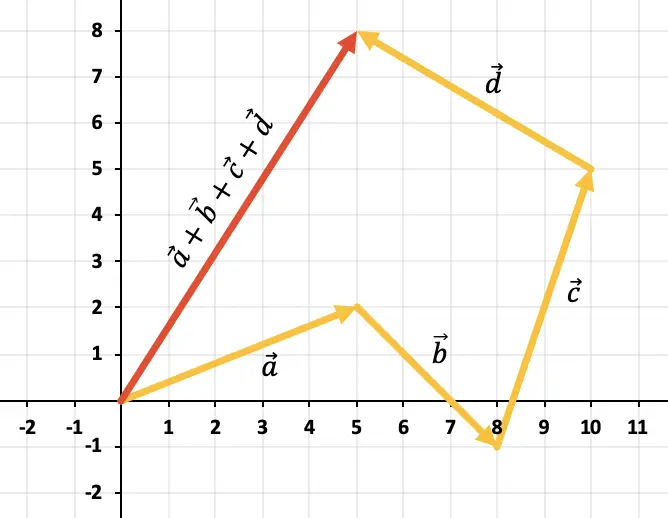
Exercício 4
Encontre numericamente a soma dos seguintes vetores:
![]()
Para somar numericamente dois vetores, você deve somar suas respectivas coordenadas:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}& =(3,-2)+(-4,6) \\[2ex] & = (3+(-4) ,-2+6)\\[2ex] & =\bm{(-1,4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6299484debe49023b686839df40f88b_l3.png)
Exercício 5
Calcule analiticamente a soma dos seguintes vetores:
![]()
Para somar vetores numericamente, você deve somar suas respectivas coordenadas:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}+\vv{c}+\vv{d}& =(-1,3)+(4,0)+(2,-5)+(3,-2) \\[2ex] & = (3,3)+(2,-5)+(3,-2) \\[2ex] & = (5,-2)+(3,-2)\\[2ex] & =\bm{(8,-4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05b7c1606bfa3d94d080163a40dc4412_l3.png)