O método dos mínimos quadrados é uma ferramenta matemática para encontrar a melhor linha reta correspondente a um conjunto de pontos . Explicamos para você de uma forma simples:
Imagine que você tem vários pontos em um gráfico espalhados aqui e ali. Você deseja encontrar uma linha reta que melhor “se ajuste” a esses pontos, de modo a minimizar a distância entre a linha e os pontos . Esta é a ideia por trás do método dos mínimos quadrados.
O método utiliza uma fórmula para calcular a equação da reta que minimiza a soma dos quadrados das diferenças entre os pontos e a reta. Ou seja, procura a reta que apresenta o menor “desvio” dos pontos.
Em termos simples, o método dos mínimos quadrados é útil para a análise dos dados obtidos durante uma investigação, com o objetivo de expressar o seu comportamento de forma linear, reduzindo os erros das informações roubadas.
Quem criou o método dos mínimos quadrados?
O método dos mínimos quadrados, ferramenta fundamental em estatística e análise de dados, é atribuído ao matemático alemão Carl Friedrich Gauss , que o propôs em 1794. Contudo, Gauss só o publicou em 1809 .
Curiosamente, o matemático francês Andrien-Marie Legendre publicou uma versão semelhante em 1805 , desenvolvendo-a de forma independente.
Ambos os matemáticos ajudaram a criar este método que tem sido amplamente utilizado em várias disciplinas para ajustar modelos aos dados observados e fazer previsões precisas.
Fórmula de mínimos quadrados
Sem dúvida, para compreender o que envolve este método, é fundamental explicar a sua fórmula e o processo da sua implementação. Aqui está uma explicação detalhada da fórmula dos mínimos quadrados:
defina o problema
Digamos que você tenha um conjunto de dados com duas variáveis, uma variável independente (x) e uma variável dependente (y), e queira ajustar uma linha reta a esses dados.
O objetivo é encontrar os valores dos coeficientes da equação da reta (interseção e inclinação) que minimiza a soma dos quadrados das diferenças entre os valores reais de y, e os valores previstos pelo linha ajustada.
Calcule a equação da reta
A equação de uma reta tem a forma y = mx + b, onde m é a inclinação eb é a interceptação y. A fórmula dos mínimos quadrados para calcular os valores myb é:
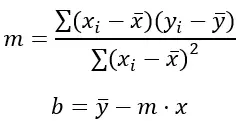
Ouro:
Σ representa a soma dos valores.
x i e y i são os valores das variáveis xey respectivamente para cada ponto de dados.
x̄ e ȳ são as médias dos valores de xey respectivamente.
(x i – x̄) e (y i – ȳ) são as diferenças entre os valores de x e y e suas respectivas médias.
(x i – x̄) 2 é o quadrado da diferença entre o valor de x e sua média.
interpretar os resultados
Depois de calcular os valores de m e b usando a fórmula, você pode usá-los para obter a equação da reta ajustada. Por exemplo, se você tiver m = 2 e b = 3, então a equação da reta ajustada seria y = 2x + 3. Isso permite fazer previsões ou estimativas dos valores de y para diferentes valores de x com base no direito ajustado.
Quando o método dos mínimos quadrados é usado?
Você provavelmente se perguntará: quando esse método é usado? É muito útil em diversas situações! Por exemplo, quando você deseja analisar dados experimentais ou de pesquisa para encontrar uma relação ou tendência .
Suponha que você esteja investigando a relação entre o preço de uma casa e seu tamanho em metros quadrados. Você pode usar o método dos mínimos quadrados para encontrar a reta que melhor se ajusta aos dados e dá uma ideia clara dessa relação.
Também é usado em economia para modelar e prever variáveis como demanda de produtos ou comportamento de preços . Além disso, na engenharia, o método dos mínimos quadrados é aplicado para ajustar modelos matemáticos a dados de teste ou simulação.
O método dos mínimos quadrados é uma ferramenta poderosa e versátil usada em muitos campos de estudo e trabalho para analisar dados e encontrar relações importantes.
Aplicações do método dos mínimos quadrados em outros teoremas
Além de seu uso em si, o método dos mínimos quadrados é muito útil em outros teoremas. Vamos ver um pouco mais sobre o assunto a seguir.
Teorema da regressão
É amplamente utilizado no teorema da regressão para encontrar a melhor reta que se ajusta a um conjunto de dados . Por exemplo, você pode usá-lo para analisar a relação entre a altura de uma planta e a quantidade de luz que ela recebe para determinar como a planta crescerá em diferentes condições de iluminação.
Interpolação de teorema
Neste caso, o método dos mínimos quadrados também é aplicado no teorema da interpolação para encontrar a função polinomial que melhor se ajusta a um conjunto de pontos. Por exemplo, você pode usá-lo para aproximar a trajetória de um objeto em movimento com base em dados de posição e tempo.
Teorema do ajuste de curva
É usado no teorema do ajuste de curva para encontrar uma curva que se ajuste a um conjunto de dados . Isto é útil em aplicações como modelagem de dados climáticos para prever mudanças climáticas ou para prever a trajetória de um projétil.
Teorema da análise de Fourier
No teorema da análise de Fourier, o método dos mínimos quadrados é usado para aproximar uma função periódica de uma série de dados discretos . Isto se aplica à sinalização de dados e à compressão de imagem e som.
Teorema da Regressão Não Linear
Finalmente, o método dos mínimos quadrados também é aplicado no teorema da regressão não linear para encontrar a melhor curva que se ajusta a um conjunto de dados que não segue uma relação linear . Por exemplo, você pode usá-lo para analisar como a concentração de um produto químico afeta a taxa de reação.
Exemplo do método dos mínimos quadrados
Para entender melhor como você pode aplicar o método dos mínimos quadrados, vejamos um exemplo abaixo.
Suponha que você tenha os seguintes dados de altura (em centímetros) de uma planta em semanas diferentes:
| Semana | altura em centímetros |
| 1 | dez |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | vinte |
Você deseja encontrar a melhor linha reta que se ajuste a esses dados para fazer uma previsão da altura futura da planta.
Etapa 1 : representar graficamente os dados
A primeira coisa a fazer é representar graficamente os dados em um gráfico de dispersão. O eixo x representará semanas e o eixo y representará a altura em centímetros. Aqui está o gráfico:
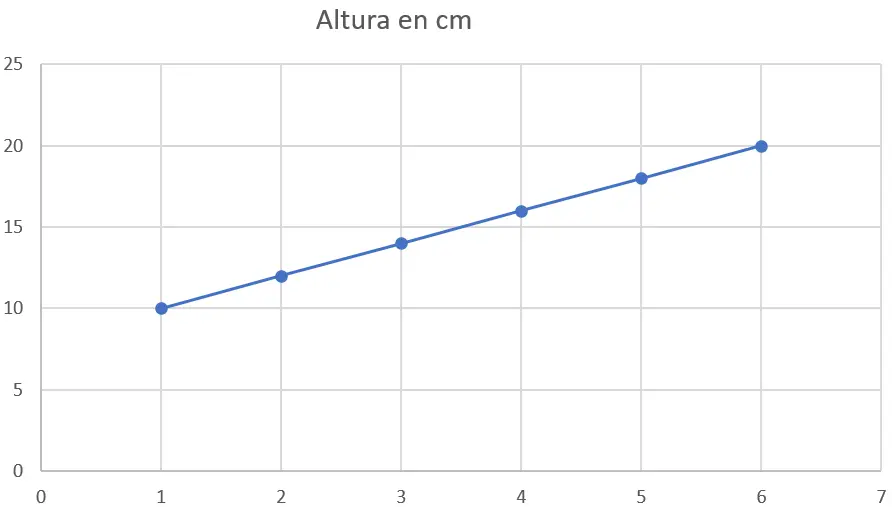
Etapa 2 : Aplicar o método dos mínimos quadrados
O método dos mínimos quadrados busca encontrar uma reta que minimize a soma dos quadrados das diferenças entre os dados reais e os valores previstos pela reta. Neste caso, a reta é representada pela equação de uma reta: y = mx + b, onde “y” é a altura, “x” são as semanas, “m” é a inclinação da reta e “b” é a interceptação y.
Para encontrar os valores de “m” e “b” que minimizam a soma dos quadrados das diferenças, são utilizadas as seguintes fórmulas:
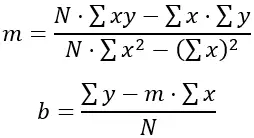
Onde N é o número de pontos de dados (neste caso, 6), Σxy é a soma das semanas vezes as alturas, Σx é a soma das semanas, Σy é a soma das alturas e Σx 2 é a soma dos quadrados das semanas .
Aplicando essas fórmulas aos dados de altura, obtemos:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
Substituindo esses valores nas fórmulas de “m” e “b”:
m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2,07
b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24
Portanto, a equação da reta que corresponde aos dados de altura é: y.