A regressão linear é um método estatístico usado para estudar a relação entre duas variáveis contínuas . A ideia principal da regressão linear é encontrar a reta que melhor se ajusta aos dados. Além disso, permite prever o valor de uma variável com base no valor de outra.
Essa linha reta é chamada de “regressão” e é usada para prever valores desconhecidos ou para entender a relação entre variáveis. Em resumo, a regressão linear é uma ferramenta para analisar e modelar a relação entre duas variáveis contínuas.
Por que a regressão linear é importante?
A regressão linear é importante porque permite modelar e analisar a relação entre duas variáveis contínuas , o que pode ser útil para prever valores futuros e identificar padrões e tendências nos dados.
Além disso, a regressão linear é uma ferramenta fundamental em estatística e na maioria das áreas de pesquisa científica e social, incluindo economia, psicologia, medicina, engenharia e física, entre outras. Também é usado na tomada de decisões de negócios e na otimização de processos na indústria e nos negócios.
Em resumo, a regressão linear é uma ferramenta poderosa e versátil que permite análise e melhor compreensão de dados e relações entre variáveis em diversas áreas de pesquisa e prática.
Quais são os tipos de regressão linear?
Existem vários tipos de regressão linear, alguns dos quais são:
regressão linear simples
A análise de regressão linear simples é uma ferramenta amplamente utilizada para estudar o efeito de uma variável independente sobre uma única variável dependente , na qual se considera que existe uma relação linear entre elas. A equação de regressão linear simples permite estimar os valores da variável dependente com base nos valores da variável independente.
A fórmula de regressão linear simples é:
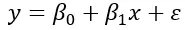
Onde, β 0 é o valor da variável dependente quando a variável independente é zero. β 1 representa a mudança na variável dependente por unidade de mudança na variável independente e ε representa o resíduo ou erro. Ou seja, a variabilidade dos dados que não pode ser explicada pela relação linear da fórmula.
Regressão linear múltipla
A regressão linear múltipla é utilizada quando há mais de uma variável independente que pode afetar a variável dependente que está sendo estudada.
A fórmula para regressão linear múltipla é:
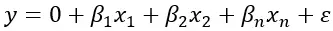
Onde Y representa a variável dependente , β 1 , β 2 , β n são as variáveis independentes que podem afetar o valor de Y, a regressão e ε representa o possível erro existente. Esta fórmula permite estimar o valor de Y com base nos valores das variáveis independentes.
Qual é a fórmula de regressão linear?
A fórmula de regressão linear é:
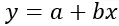
Ouro:
y é a variável dependente (ou resposta) a ser prevista
x é a variável independente (ou preditora) usada para fazer a previsão
a é a interceptação (ou o ponto onde a linha de regressão cruza o eixo Y quando x=0)
b é a inclinação da linha de regressão (indicando a taxa de variação de y para cada alteração de x)
Para encontrar os valores de a e b, utilizamos o método dos mínimos quadrados que busca minimizar a soma dos erros quadráticos entre os valores observados e os valores previstos pela reta de regressão.
Aqui estão as fórmulas:
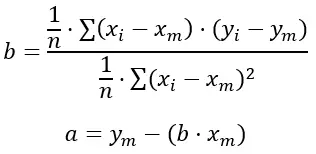
Ouro:
n é o número total de conjuntos de dados que temos.
x i e y i são os valores que tomamos no somatório.
x m e y m são os valores médios de cada variável.
Como aplicar o método de regressão linear?
O método de regressão linear pode ser aplicado seguindo as etapas abaixo:
- Coletar dados : A primeira coisa a fazer é coletar os dados de seu interesse. Por exemplo, se você deseja estudar a relação entre salário e idade de um grupo de pessoas, é necessário coletar informações sobre o salário e a idade de cada uma delas.
- Traçar os dados – A seguir, é necessário traçar os dados em um plano cartesiano, onde a variável independente (neste caso, idade) é colocada no eixo horizontal e a variável dependente (salário) é colocada no eixo vertical.
- Determine a linha de regressão : A linha de regressão que melhor se ajusta aos dados deve ser determinada. Esta linha é obtida a partir da fórmula de regressão linear, que é calculada a partir dos dados estatísticos da amostra .
- Avaliar a qualidade do ajuste – É importante avaliar até que ponto a linha de regressão se ajusta aos dados. Isso pode ser feito usando medidas estatísticas.
- Faça previsões – Finalmente, as previsões podem ser feitas usando a linha de regressão resultante. Por exemplo, se você quiser prever o salário de uma pessoa de 30 anos, você usaria a fórmula de regressão linear e substituiria o valor da idade nela.
É importante observar que essas etapas podem variar ligeiramente dependendo do tipo de regressão linear utilizada e do software estatístico utilizado.
Para que é usada a regressão linear?
A regressão linear é usada quando você deseja analisar a relação entre duas variáveis , onde uma variável pode afetar o valor de outra variável. Portanto, a regressão linear pode ser usada para compreender como uma variável independente afeta uma variável dependente e para prever o valor da variável dependente com base na variável independente.
É importante notar que a regressão linear assume que a relação entre as duas variáveis é linear , o que significa que a mudança na variável dependente é proporcional à mudança na variável independente.
Portanto, a regressão linear deve ser utilizada quando se suspeita de uma relação linear entre as duas variáveis. Se esta condição não for satisfeita, poderá ser mais apropriado utilizar outros modelos de regressão não linear ou diferentes métodos estatísticos.
Quais são as aplicações da regressão linear?
A regressão linear é utilizada em uma ampla variedade de aplicações em áreas como estatística, economia, engenharia, ciências sociais, biologia, entre outras. Aqui estão algumas das aplicações mais comuns de regressão linear:
- Análise de Tendências – Para analisar tendências em dados históricos e prever tendências futuras.
- Previsão – Prever o valor futuro de uma variável com base em valores passados de uma ou mais variáveis.
- Pesquisa de mercado : estudo da relação entre a demanda de um produto e seu preço.
- Análise Financeira – Estudar a relação entre receitas e despesas de uma empresa e prever resultados financeiros futuros.
- Estudos epidemiológicos : estudam a relação entre a exposição a um fator de risco e a probabilidade de desenvolver uma doença.
- Ciências Sociais – Estudar a relação entre duas ou mais variáveis em áreas como psicologia, sociologia e ciência política.
- Pesquisa Operacional – A regressão linear é usada para modelar e otimizar sistemas complexos em áreas como engenharia industrial e logística.
- Ciências Ambientais – Utilizadas para estudar a relação entre fatores ambientais e efeitos nos ecossistemas.
O que são resíduos na regressão linear?
Os resíduos na regressão linear são a diferença entre os valores observados da variável dependente e os valores previstos pelo modelo de regressão linear . Em outras palavras, é a distância vertical entre os pontos de dados reais e a linha de regressão.
A ideia por trás dos resíduos é que, se a linha de regressão se ajustar bem aos dados, os resíduos deverão ser pequenos e aleatórios. Se os resíduos forem grandes ou seguirem determinado padrão, isso pode ser sinal de que a relação entre as variáveis não é linear ou de que o modelo de regressão linear não está ajustado aos dados.
Os resíduos também são usados para avaliar a precisão do modelo de regressão linear e para identificar valores discrepantes ou pontos de dados influentes que podem afetar a qualidade do modelo.
Posso executar a regressão linear com mais de uma variável dependente?
Na regressão linear, a variável dependente é sempre uma variável única. No entanto, você pode ter mais de uma variável independente. Neste caso, falaríamos de regressão linear múltipla .
Na regressão linear múltipla, o objetivo é estudar o efeito de múltiplas variáveis independentes sobre uma única variável dependente.
Como posso interpretar coeficientes na regressão linear?
Na regressão linear, os coeficientes representam a inclinação e a interceptação da linha de regressão . A inclinação indica a mudança na variável dependente por unidade de mudança na variável independente, enquanto o intercepto representa o valor da variável dependente quando a variável independente é igual a zero.
Exemplos Numéricos de Regressão Linear
Um exemplo simples pode ser o seguinte:
Suponha que temos os seguintes dados de idade e altura para um grupo de pessoas:
| anos de idade) | Altura (cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| Quatro cinco | 190 |
Queremos determinar se existe uma relação entre a idade e a altura dessas pessoas. Para fazer isso, usaremos regressão linear.
Primeiro, podemos desenhar umgráfico estatístico com os dados (neste caso recomendamos o uso de um gráfico de dispersão):
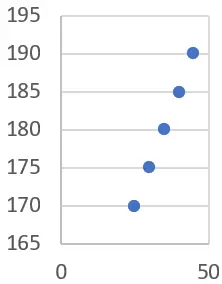
Podemos perceber que há uma tendência clara de que à medida que a idade aumenta, a altura também aumenta. Podemos confirmar isso calculando a linha de regressão linear.
Calculando os coeficientes da reta de regressão linear com as fórmulas que vimos anteriormente, obtemos:
em = 145
b = 1
Portanto, a equação da reta de regressão linear é:
Altura = 145 + 1 Idade
Podemos usar esta equação para prever a altura de uma pessoa com base na sua idade. Por exemplo, se uma pessoa tem 32 anos, podemos prever que a sua altura seria:
Altura = 145 + 1 32 = 177 cm