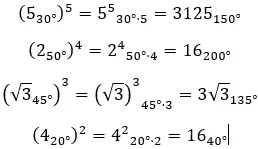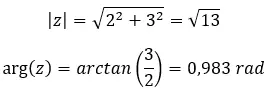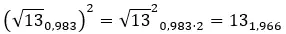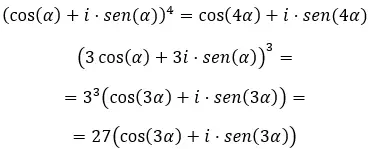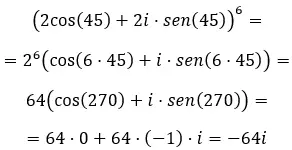Resolver as potências dos números complexos é algo bastante fácil de fazer, se você conhecer o método correto. Portanto, neste artigo explicaremos como resolver potências complexas de três maneiras: para números complexos na forma binomial, na forma polar e na forma trigonométrica.
Como resolver a potência de um número complexo?
Como dissemos na introdução, podem surgir três situações quando se opera com poderes complexos. A primeira e mais simples é quando recebemos o número na forma polar . A segunda é quando recebemos o número na forma binomial e a terceira é quando recebemos o número na forma trigonométrica.
Ou seja, ao operar com complexos na forma polar, o exercício pode ser resolvido mais rapidamente. Portanto, é recomendável converter o número em questão para a forma polar. Mas, na verdade, todos os métodos são fáceis de resolver . Dito isto, explicaremos como todos os casos são resolvidos e ofereceremos um exercício.
Potências de números complexos na forma polar
Quando queremos resolver potências complexas na forma polar , simplesmente elevamos o módulo para qualquer e multiplicamos o argumento por n. Expressado matematicamente, obtemos a seguinte fórmula:
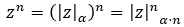
Aqui estão alguns exemplos, para que você possa tentar resolvê-los sozinho:
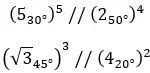
Potências de números complexos na forma binomial
Por outro lado, quando queremos resolver potências complexas na forma binomial , podemos utilizar dois métodos diferentes. A primeira trata de resolver a potência de forma “algébrica” (resolvendo como se eu fosse uma variável). E o segundo sistema é converter a forma binomial em polar e depois seguir o procedimento anterior.
Se você não sabe como passar da forma binomial para a polar, explicamos isso muito claramente em nosso artigo sobre números complexos . Porém, agora veremos isso rapidamente com um exemplo.
Tente resolver a seguinte potência complexa: (2 + 3i) 2 .
Potências de números complexos na forma trigonométrica
Finalmente, quando queremos resolver potências complexas na forma trigonométrica , devemos usar a conhecida fórmula de de Moivre. Que está escrito da seguinte forma:
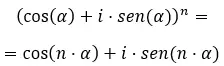
Conhecendo esta fórmula, tente resolver os seguintes exercícios: