Neste artigo explicamos como salvar o limite de uma função quando ela dá incerteza 0/0. Além disso, você poderá praticar com exercícios resolvidos sobre a indeterminação de zero entre zero.
Como resolver a indeterminação zero entre zero (0/0)
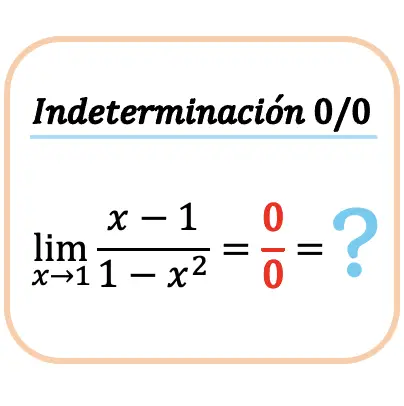
Veremos então como calcular o limite de uma função quando ela dá indeterminação zero entre zero (0/0). Para fazer isso, calcularemos um exemplo passo a passo:
![]()
Primeiro tentamos calcular o limite substituindo o valor de x na função:
![]()
Mas obtemos a indeterminação 0 dividida por 0.
Quando o limite de uma função pontual dá a incerteza 0/0 , é necessário fatorar os polinômios do numerador e do denominador e depois simplificar os fatores comuns.
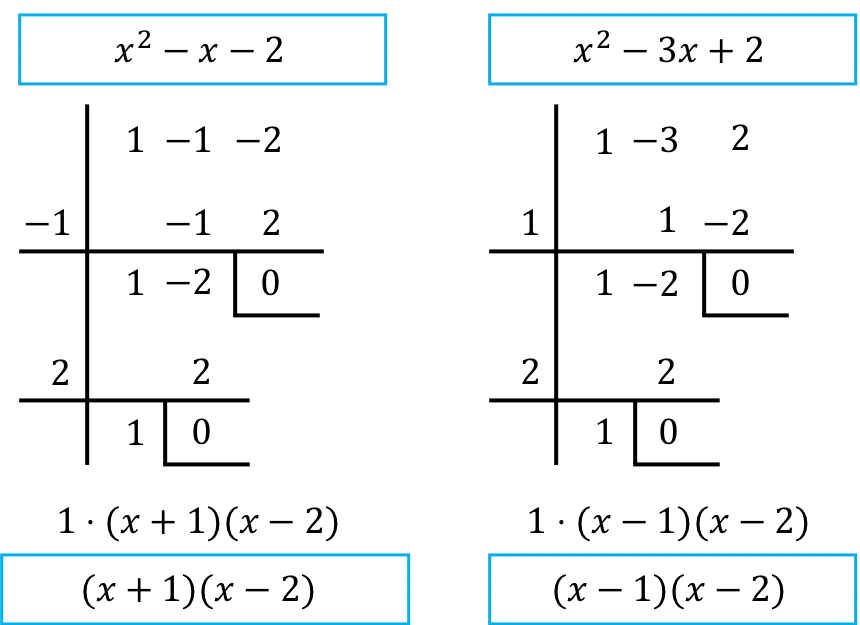
Devemos, portanto, fatorar os polinômios do numerador e denominador da fração. Para fazer isso, usamos a regra de Ruffini:
➤ Se você não sabe como fatorar um polinômio , recomendamos que veja a explicação em nosso site especializado em polinômios: www.polinomios.org
Assim, uma vez fatorados os polinômios, o limite é o seguinte:
![]()
Podemos agora simplificar o limite eliminando os fatores que se repetem no numerador e no denominador da fração:
![]()
E finalmente, recalculamos o limite:
![]()
Como você pode ver, uma vez fatorados e simplificados os polinômios, é muito fácil encontrar a solução no limite.
Indeterminação 0/0 com raízes
Acabamos de ver como as indeterminações 0/0 das funções racionais são resolvidas. Porém, se o limite for de uma função irracional (ou radical), a indeterminação 0/0 é resolvida de forma diferente.
![]()
Primeiro, tentamos resolver o limite realizando as seguintes operações:
![]()
Mas obtemos zero sobre zero indeterminação.
Se o limite de uma função com raízes dá indeterminação 0/0 , deve-se multiplicar o numerador e o denominador da fração pelo conjugado da expressão radical.
➤ Lembre-se que o conjugado é a mesma expressão irracional, mas com o sinal do meio modificado.
A seguir, multiplicamos o numerador e o denominador da fração pelo conjugado da expressão radical:
![]()
Dentro deste tipo de limites, ao realizar este passo obteremos sempre uma identidade notável que podemos simplificar. Neste caso, no denominador temos o produto de uma soma e uma diferença, portanto:
![]()
![]()
Simplificamos o fator que se repete no numerador e no denominador:
![]()
E desta forma podemos encontrar o resultado do limite:
![]()
Exercícios resolvidos sobre indeterminação 0/0
Abaixo preparamos vários exercícios resolvidos passo a passo sobre os limites de funções que fornecem indeterminações 0/0. Você pode tentar fazê-los e depois verificar a solução.
Não se esqueça que você pode nos tirar qualquer dúvida sobre como resolver limites nos comentários!
Exercício 1
Calcule o limite da seguinte função racional no ponto x=-2.
![]()
Logicamente, primeiro tentamos resolver o limite:
![]()
Mas acabamos com indeterminação 0/0. Devemos, portanto, fatorar os polinômios do numerador e do denominador:
![]()
Agora simplificamos a fração removendo os parênteses que se repetem no numerador e no denominador:
![]()
E por fim, recalculamos o limite com a fração simplificada:
![]()
Exercício 2
Resolva o limite da seguinte função quando x se aproxima de -1:
![]()
Primeiro tentamos resolver o limite normalmente:
![]()
Mas obtemos a indeterminação 0 entre 0. Devemos, portanto, fatorar os 2 polinômios da fração:
![]()
Agora podemos simplificar os polinômios:
![]()
E resolvemos o limite:
![]()
Exercício 3
Determine a solução do limite da seguinte função radical:
![]()
Primeiro, verificamos se o limite dá algum tipo de indeterminação:
![]()
O limite dá a indeterminação zero dividido por zero e temos uma raiz na função. Devemos, portanto, multiplicar o numerador e o denominador da fração pelo conjugado da expressão radical:
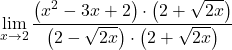
O denominador corresponde ao desenvolvimento da identidade notável do produto de uma soma e uma diferença, podemos portanto simplificá-lo:
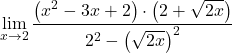
![]()
No entanto, ainda não podemos simplificar os termos da fração. Devemos, portanto, fatorar os polinômios:
![]()
Desta forma podemos simplificar a fração:
![]()
E agora podemos determinar o resultado do limite:
![]()
Exercício 4
Calcule o limite quando x se aproxima de 0 da seguinte função radical:
![]()
Primeiro, tentamos calcular o limite da função como sempre fazemos:
![]()
Mas obtemos a forma indeterminada de 0/0. Portanto, multiplicamos o numerador e o denominador da função pelo conjugado da expressão irracional:
![]()
Aplicamos a fórmula de identidade notável correspondente para simplificar o denominador:
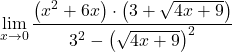
![]()
![]()
Agora fatoramos o binômio do numerador tomando o fator comum:
![]()
Simplificamos os fatores que se repetem no numerador e no denominador da função:
![]()
E, finalmente, resolvemos o limite da função:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b4874df2f48ad131d48c4e5923a5b02_l3.png)
Exercício 5
Resolva o seguinte limite usando o método de indeterminação 0/0:
![]()
➤ Veja: como calcular os limites laterais de uma função
Primeiro tentamos resolver o limite:
![]()
Mas no limite obtemos indeterminação zero sobre zero. Portanto, fatoramos os polinômios do numerador e do denominador:
![]()
Agora simplificamos a fração eliminando os fatores que se repetem no numerador e no denominador:
![]()
E calculamos o limite novamente:
![]()
Mas agora nos encontramos com a indeterminação de um número dividido por 0. Devemos, portanto, calcular os limites laterais da função quando x tende a -1.
Primeiro resolvemos o limite lateral da função no ponto x=-1 à esquerda:
![]()
E então calculamos o limite lateral da função no ponto x=-1 à direita:
![]()
Portanto, como os dois limites laterais não coincidem, o limite da função em x=-1 não existe:
![]()