Você certamente já ouviu falar do conjunto dos números imaginários ou da unidade imaginária. É um conceito matemático que surge da necessidade matemática de expressar números que não pertencem aos números reais .
O que são números imaginários?
Números imaginários são aqueles que, quando elevados ao quadrado, dão um número negativo . Portanto, estes são valores equivalentes à raiz quadrada de um número negativo. Por exemplo, a unidade imaginária (o número i) é igual à raiz quadrada de -1.
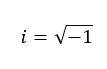
Esses números não pertencem aos números reais porque no conjunto real as raízes negativas não podem ser resolvidas. É aqui que reside a importância do cenário imaginário. Este conjunto foi inventado para poder lidar com raízes negativas e poder resolver todas aquelas equações e problemas quadráticos que “não têm solução”, porque nos dão uma raiz negativa.
Para evitar confusão, é importante distinguir entre números imaginários e números complexos . Complexos são números compostos por um número real e um número imaginário . Portanto, os imaginários são uma subcategoria de complexos, que não possuem parte real. Na tabela a seguir você poderá apreciar melhor as diferenças.
| número complexo | festa real | parte da imaginação | Descrição |
| 4+7i | 4 | 7i | Complexo |
| 3 | 3 | 0 | puro real |
| 2i | 0 | 2i | Pura Imaginação |
Para finalizar a situação deste conjunto digital, podemos visualizar na imagem a seguir uma estrutura de todos os conjuntos. Como podemos ver, os números complexos abrangem todos os tipos de números , estes por sua vez podem ser divididos em números reais e números imaginários puros (que são os que tratamos neste artigo).

Exemplos de números imaginários
Da unidade imaginária (i), podemos deduzir outros números imaginários. Você só precisa aplicar a seguinte fórmula:
m = ri
Onde m é um número imaginário, r é um número real e i é a unidade imaginária. Na imagem a seguir você pode ver como obtemos diferentes imaginários a partir de raízes negativas.
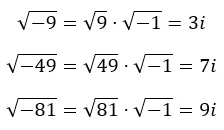
Na verdade, podemos extrapolar para a seguinte expressão:
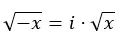
Propriedades de números imaginários
Os números imaginários têm uma série de propriedades muito interessantes . Alguns já falamos no início deste artigo e outros não:
- Os imaginários não pertencem ao conjunto das realidades, porque são números que fisicamente não existem e não podem ser representados na nossa realidade.
- Estes são valores equivalentes a raízes negativas.
- Eles podem ser representados graficamente na linha imaginária.
- As potências imaginárias (este é um conceito que explicaremos na próxima seção) são de grande ajuda na simplificação de cálculos numéricos envolvendo valores imaginários.
- A fórmula de Euler é uma expressão que permite relacionar números imaginários com números reais.
Operações com números imaginários
Agora que você conhece todas as características importantes dos números imaginários, é hora de aprender como resolver operações com eles. Para operar com valores imaginários , você deve seguir os mesmos passos que segue para operar com valores reais, exceto que deve levar em consideração um conceito: potências imaginárias.
poderes imaginativos
Os números imaginários possuem uma propriedade muito interessante que ocorre quando multiplicamos a unidade imaginária por ela mesma. Ou seja, isso acontece quando você faz potências de unidade imaginária . Se anotarmos as potências, como na lista a seguir, um padrão pode ser descoberto:
eu 0 = 1
eu 1 = eu
eu 2 = eu · eu = ( √ -1) · ( √ -1) = -1
eu 3 = eu 2 eu = (-1) eu = -eu
eu 4 = eu 2 eu 2 = (-1) (-1) = 1
Conhecer este conceito nos tornará muito mais fácil resolver operações com números imaginários, pois poderemos simplificar operações difíceis e torná-las um pouco mais fáceis. Além disso, o bom desses poderes é que eles se repetem indefinidamente. Podemos ver isso se adicionarmos mais alguns poderes:
eu 5 = eu
eu 6 = -1
eu 7 = -eu
eu 8 = 1
etc.
E com potências negativas isso também acontece.
Operações aritméticas com números imaginários
A seguir daremos um exemplo de cada operação aritmética básica, para que você possa ver os cálculos de números imaginários resolvidos.
- Somar números imaginários: é exatamente o mesmo que somar números reais, só não se esqueça de somar o i.
4i + 3i = 7i
- Subtração de números imaginários: As subtrações também são resolvidas da mesma forma que no conjunto real.
4i – 3i = eu
- Multiplicação de números imaginários: neste caso devemos ter em mente as potências imaginárias que mencionamos anteriormente.
3i 4i = 12 eu 2 = 12 (-1) = -12
- Divisão de números imaginários: neste tipo de divisão também devemos estar atentos, caso encontremos uma potência imaginária, o que nos permite simplificar a operação.
12i ÷ 4i = 3
Equações com números imaginários
Como dissemos antes, quando resolvemos equações do conjunto real, às vezes obtemos raízes negativas e, portanto, as equações “não têm solução” . Mas, agora que conhecemos os imaginários, podemos resolver estas equações. Vejamos um exemplo:
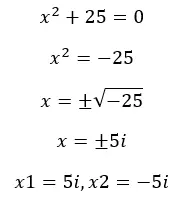
Para que são usados os números imaginários?
Os números imaginários surgem da necessidade de poder expressar valores que estão fora do conjunto real. É por isso que, a princípio, pode parecer que eles não têm muitos aplicativos úteis . Mas a verdade é que é exatamente o contrário. Porque quando os combinamos com os reais, obtemos os números complexos.
E estes têm muitas aplicações. São utilizados para estudar corrente alternada (por apresentar valores negativos), seu uso também é muito difundido na área de ondas (que tem aplicações em física, eletrônica de telecomunicações e mecânica quântica). Entre muitos outros usos.
Além disso, muitas vezes acontece que quando você resolve uma equação quadrática , o valor lhe dá uma raiz negativa e você não consegue operar… Com imaginários você pode resolvê-los . Assim, como conclusão, podemos dizer que é um conjunto que nos permite ampliar nossos conhecimentos mais abstratos.