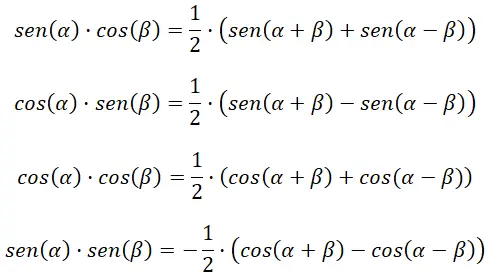Identidades trigonométricas são igualdades entre diferentes funções trigonométricas. Graças a estas equivalências trigonométricas, podemos deduzir uma certa razão trigonométrica com base em qualquer outra. Portanto, é necessário conhecer as fórmulas dessas razões para compreender as fórmulas das identidades trigonométricas. Caso não os conheça no seu caso, recomendamos que visite o último link.
Tabela de identidades trigonométricas
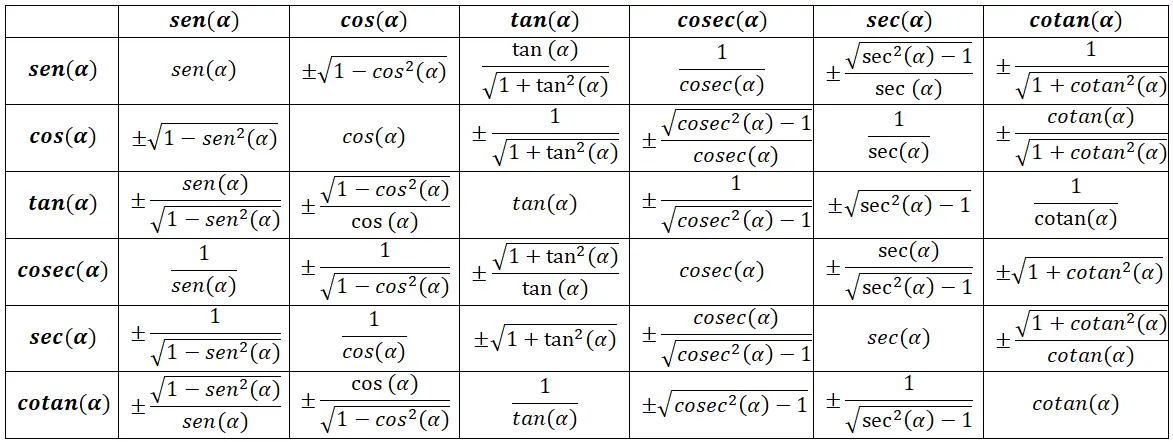
Identidades trigonométricas fundamentais
Há uma série de identidades trigonométricas básicas que são consideradas as mais importantes porque fornecem a base teórica para as demais. Estes são os mais comuns de encontrar e provavelmente os mais fáceis de lembrar, pois são bastante intuitivos. Lembre-se que todas as fórmulas serão baseadas na seguinte imagem:

Identidade trigonométrica fundamental
A primeira identidade de todas é conhecida como identidade trigonométrica fundamental , também conhecida como relação entre seno e cosseno. Abaixo está sua prova matemática: sin² (α) + cos² (α) = 1.
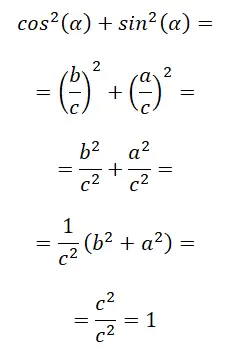
Na última etapa aplicamos basicamente o teorema de Pitágoras, pois c² = a² + b², ficamos então com c² / c² que é igual a 1. Concluindo, podemos afirmar que: sin² (α) + cos² (α) = 1.
Relação entre secante e tangente (secante ao quadrado)
Em segundo lugar, temos uma identidade trigonométrica que relaciona a secante com a tangente, sua expressão é a seguinte: sec² (α) = 1 + tan² (α) . Na imagem a seguir você pode ver algumas fórmulas de lembrete que compõem esta identidade e a seguir o procedimento a seguir para chegar à fórmula final:
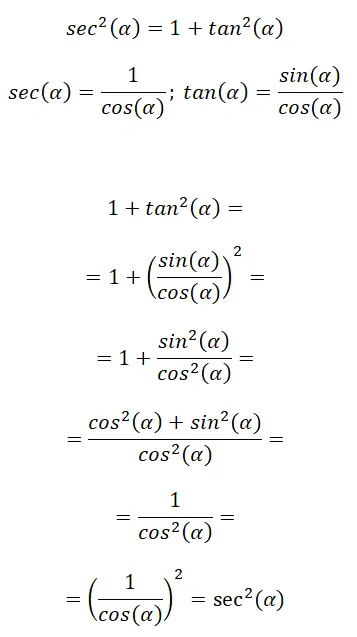
Nesse caso, usamos as fórmulas de razão trigonométrica para encontrar outras razões. Concluindo, podemos dizer que: sec²(α) = 1 + tan²(α).
Relação entre cossecante e cotangente (cosecante ao quadrado)
A partir da definição de cossecante e cotangente podemos encontrar uma ligação na fórmula da tangente, é graças a isso que podemos deduzir outra identidade trigonométrica: cosec² (α) = 1 + cotg² (α) .
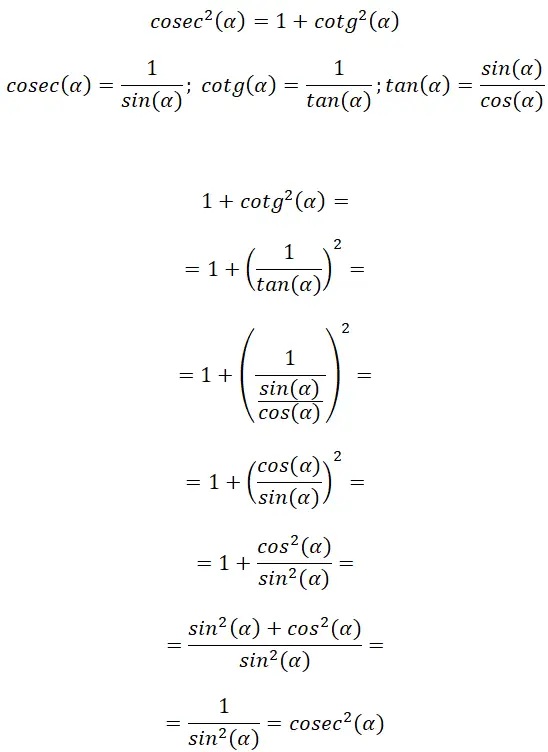
Com esta demonstração podemos verificar que: cosec² (α) = 1 + cotg² (α). Além disso, podemos perceber que esta relação tem alguma semelhança com a anterior, o que se deve à semelhança entre tangente e cotangente.
Razões trigonométricas do ângulo de soma e do ângulo de subtração
As razões de soma ou subtração de ângulos são um tipo de identidade obtida pelo cálculo das razões trigonométricas da adição ou subtração de dois ângulos. Por exemplo, se quisermos calcular o seno de 90 + 60, existe uma série de fórmulas que facilitam esse cálculo. Abaixo está uma lista com todas as fórmulas para identidades trigonométricas deste estilo:
Seno da soma dos ângulos: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Seno da subtração do ângulo: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Cosseno da soma dos ângulos: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Subtração do cosseno angular: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Tangente da soma dos ângulos: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
Subtração de tangente angular: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))
É óbvio que calcular o seno de 150º é mais fácil do que usar as fórmulas que acabamos de explicar para calcular o seno de (90º + 60º). Então, por que essas fórmulas são importantes? Bem, a resposta é que estas identidades permitem-nos calcular as razões trigonométricas de ângulos complexos a partir de ângulos mais simples. Portanto, se memorizarmos as razões dos ângulos notáveis (mais relevantes), não precisaremos usar a calculadora para calcular as razões de ângulos mais complexos como 150º.
Razões trigonométricas de ângulo duplo
Quando queremos calcular as razões trigonométricas de um ângulo duplo (2α) , podemos fazê-lo por meio de uma série de identidades. Mais precisamente, podemos fazer isto através de fórmulas muito semelhantes às que acabamos de discutir na secção anterior. Visto que, se mudarmos β para α, nas expressões anteriores, ficamos com (α + α), que equivale a (2α). Com isso em mente, podemos derivar as seguintes identidades:
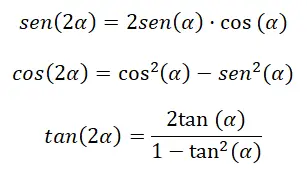
Você pode ver as demonstrações abaixo:
Seno do ângulo duplo: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Cosseno do ângulo duplo: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Ângulo tangente duplo: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
Razões trigonométricas do meio ângulo
Além disso, existem identidades que nos permitem calcular as razões trigonométricas do meio ângulo (α/2) :
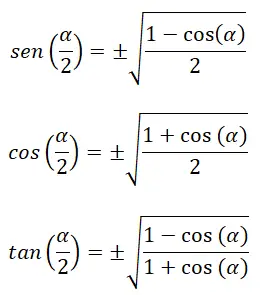
Entre as seguintes fórmulas já conhecidas:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
Se fizermos β = α/2, então podemos provar essas identidades, subtraindo as duas expressões no caso do seno, somando-as no caso do cosseno, e dividindo as duas fórmulas obtidas (a do seno e a do cosseno) no caso da tangente. Porém, resta isolar a proporção que queremos calcular nas fórmulas que obtemos a seguir:
Meio ângulo seno: 1 – cos (α) = 2 sen² (α/2); sen² (α/2) = (1 – cos (α)) ÷ 2
Cosseno de meio ângulo: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
Razões trigonométricas do ângulo triplo
No caso de termos um ângulo triplo (3α) , também podemos utilizar certas identidades para calcular suas razões trigonométricas. Essas identidades vêm das seguintes fórmulas já explicadas: identidades de ângulos duplos, identidades de soma de ângulos e a identidade fundamental da trigonometria.
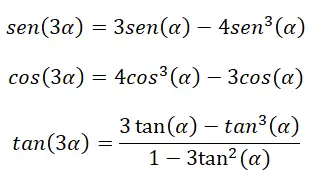
Para provar essas identidades, devemos usar as fórmulas da soma dos ângulos:
Seno da soma dos ângulos: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Cosseno da soma dos ângulos: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Portanto, se aplicarmos as fórmulas dos ângulos duplos nas expressões que acabamos de falar e aplicarmos a identidade fundamental da trigonometria, poderemos provar as identidades. Vale ressaltar que o uso da identidade trigonométrica fundamental nos permite converter todas as razões da expressão em uma. É por isso que a fórmula do seno do ângulo triplo é composta apenas por senos e a do cosseno contém apenas cossenos. Abaixo você confere o procedimento completo:
Seno do ângulo triplo: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sen (α) cos² (α) – sin³ (α) + 2 sen (α) cos² (α) =
= pecado (α) · (1 – pecado² (α)) – pecado³ (α) + 2 pecado (α) · (1 – pecado² (α)) =
= pecado (α) – pecado³ (α) – pecado³ (α) + 2 pecado (α) – 2 pecado³ (α) =
= 3 sen (α) – 4 sen³ (α)
Cosseno do ângulo triplo: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Por fim, a tangente do ângulo triplo pode ser calculada de duas formas: a primeira dividindo a fórmula do seno pela fórmula do cosseno e a segunda substituindo a expressão da tangente do ângulo duplo, na seguinte fórmula à tangente do ângulo duplo ângulo de soma: tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) tan (2α)).
Identidades trigonométricas de acordo com o tipo de ângulo
É importante comentar uma série de fórmulas que são de certa forma regras que permitem o cálculo direto e rápido de razões trigonométricas. Na verdade, também podem ser consideradas identidades trigonométricas, pois apresentam as mesmas características de todas as expressões de que acabamos de falar. Mais precisamente, estas fórmulas permitem-nos determinar as relações trigonométricas de um ângulo a partir da relação que tem com outro ângulo.
ângulos complementares
Os ângulos complementares (α e β ) são aqueles que possuem soma igual a 90º, portanto quando os somamos obtemos um ângulo reto. Para determinar que α é o ângulo complementar de β , devemos resolver uma equação muito simples: α = 90 – β , se o resultado desta equivalência for concordante, então podemos afirmar que são complementares. Graças a estas identidades podemos deduzir as razões trigonométricas de um ângulo em relação às do outro.
Seno do ângulo complementar: sin (90º – α) = cos (α)
Cosseno do ângulo complementar: cos (90º – α) = sin (α)
Tangente do ângulo complementar: tan (90º – α) = cotan (α)
Cossecante do ângulo complementar: cosec (90º – α) = seg (α)
Secante do ângulo complementar: sec (90º – α) = cosec (α)
Cotangente do ângulo complementar: cotan (90º – α) = tan (α)
ângulos adicionais
Os ângulos suplementares (α e β ) são aqueles que possuem soma igual a 180º ou π radianos, podemos portanto deduzir a fórmula α + β = 180º. Ou, em outras palavras, se o ângulo suplementar de α for β , então a seguinte expressão β = 180 – α deve ser satisfeita. Então você pode ver a lista de identidades que podemos deduzir destes ângulos:
Seno do ângulo suplementar: sin (180º – α) = sin (α)
Cosseno do ângulo adicional: cos (180º – α) = -cos (α)
Tangente do ângulo suplementar: tan (180º – α) = -tan (α)
Cosecante do ângulo adicional: cosec (180º – α) = cosec (α)
Secante do ângulo suplementar: seg (180º – α) = -sec (α)
Cotangente do ângulo suplementar: cotan (180º – α) = -cotan (α)
ângulos conjugados
Os ângulos conjugados (α e β ) são aqueles que possuem soma igual a 360º ou 2π radianos, por isso podemos deduzir a fórmula α + β = 360º. E a partir desta primeira fórmula podemos expressar um dos ângulos em termos do outro da seguinte forma: α = 360º – β ou β = 360º – α. Mostraremos agora as igualdades dos ângulos conjugados:
Seno do ângulo conjugado: sin (360º – α) = – sin (α)
Cosseno do ângulo conjugado: cos (360º – α) = cos (α)
Tangente do ângulo conjugado: tan (360º – α) = – tan (α)
Cosecante do ângulo conjugado: cosec (360º – α) = – cosec (α)
Secante do ângulo conjugado: seg (360º – α) = seg (α)
Cotangente do ângulo conjugado: cotan (360º – α) = – cotan (α)
ângulos opostos
Ângulos opostos ou ângulos negativos (α e β ) são aqueles que possuem o mesmo valor numérico, mas possuem sinais diferentes, um exemplo desse tipo de ângulo é 30º e -30º. Deve-se lembrar que o sinal negativo indica que a rotação é no sentido horário, enquanto o ângulo positivo gira no sentido anti-horário.
Seno do ângulo oposto: sin (-α) = – sin (α)
Cosseno do ângulo oposto: cos (-α) = cos (α)
Tangente do ângulo oposto: tan (-α) = – tan (α)
Cossecante do ângulo oposto: cosec (-α) = – cosec (α)
Secante do ângulo oposto: sec (-α) = seg (α)
Cotangente do ângulo oposto: cotan (-α) = – cotan (α)
Ângulos que diferem de 90º ou ângulos mais/menos π/2
Ângulos que diferem em 90º ou ângulos mais/menos π/2 (α e β ) são aqueles que possuem diferença de 90º. Portanto, podem ser expressos como β – α = 90º, onde β é 90º maior que α . Esses ângulos também possuem uma série de fórmulas que relacionam as razões trigonométricas dos dois ângulos.
Seno do ângulo que difere de 90º: sin (90º + α) = cos (α)
Cosseno do ângulo que difere de 90º: cos (90º + α) = -sin (α)
Tangente do ângulo que difere de 90º: tan (90º + α) = – cotan (α)
Cossecante do ângulo que difere de 90º: cosec (90º + α) = seg (α)
Secante do ângulo que difere de 90º: sec (90º + α) = -cosec (α)
Cotangente do ângulo que difere de 90º: cotan (90º + α) = -cotan (α)
Ângulos que diferem de 180º ou ângulos mais/menos π
Os ângulos mais/menos π (α e β ) são equivalentes a ângulos que diferem em 180º. Portanto, podem ser expressos através da seguinte fórmula: β – α = 180º, onde β 180º é maior que α . A seguir, mostramos as identidades trigonométricas que relacionam as razões trigonométricas desses ângulos:
Seno do ângulo que difere de 180º: sin (180º + α ) = -sin ( α )
Cosseno do ângulo que difere de 180º: cos (180º + α ) = -cos ( α )
Tangente do ângulo que difere de 180º: tan (180º + α ) = tan ( α )
Cosecante do ângulo que difere de 180º: cosec (180º + α ) = -cosec ( α )
Secante do ângulo que difere de 180º: sec (180º + α ) = -sec ( α )
Cotangente do ângulo que difere de 180º: cotan (180º + α ) = cotan ( α )
Transformações de razões trigonométricas
Finalmente, existem identidades trigonométricas que nos permitem expressar uma determinada razão trigonométrica por meio de outras operações . Portanto, se tivermos uma soma de rácios e quisermos expressá-la como um produto, podemos recorrer a estas fórmulas. Embora, infelizmente, não exista uma expressão para todas as operações aritméticas, só é possível passar da adição ou subtração ao produto e vice-versa .
Converter adição ou subtração em produto
As quatro fórmulas a seguir nos ajudam a calcular a adição e subtração de funções trigonométricas:
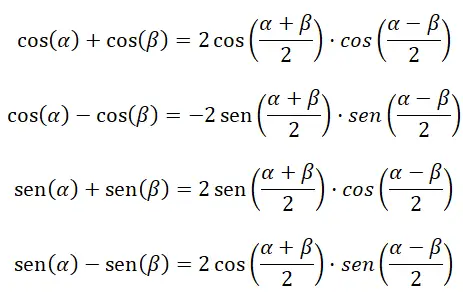
Transforme o produto em adição ou subtração
As quatro fórmulas a seguir nos ajudam a calcular os produtos de funções trigonométricas: