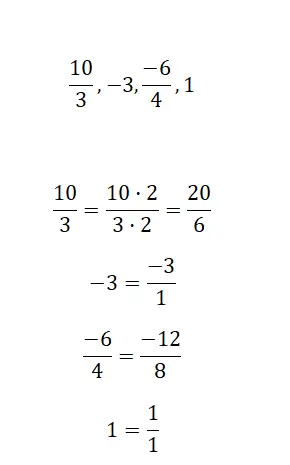Neste artigo você encontrará uma explicação sobre frações equivalentes ou frações iguais que é muito completa e fácil de entender. Mais especificamente, falaremos sobre a sua definição, como calculá-las e como saber se duas frações são equivalentes. Assim você acabará sabendo tudo o que precisa para resolver exercícios de frações equivalentes como os que apresentaremos no final. Dito isto, vamos começar com o tema.
Calculadora de frações equivalentes
Com a ajuda desta calculadora de frações equivalentes, você poderá verificar se duas frações são iguais, sem precisar fazer nenhum cálculo. O seu funcionamento é muito simples, basicamente basta inserir os valores correspondentes aos dois numeradores e aos dois denominadores e clicar no botão “Calcular”.
O que são frações equivalentes?
Frações equivalentes são aquelas que expressam o mesmo valor numérico , portanto, são frações que equivalem ao mesmo resultado, mesmo que tenham numerador e denominador diferentes. Isso significa que possuem uma relação proporcional, que pode ser de dois tipos: ampliada ou simplificada. A seguir mostramos um exemplo gráfico de frações equivalentes para que o conceito seja melhor compreendido.
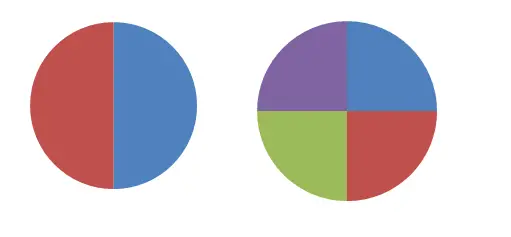
Na imagem anterior você pode ver dois círculos divididos em duas e quatro partes. Se tentarmos definir a primeira por uma fração, diremos que cada parte é igual a 1/2 do todo, enquanto na segunda figura utilizaremos a fração 1/4. Obviamente, essas duas frações não são equivalentes , pois representam quantidades diferentes. Mas, se pegarmos dois pedaços do segundo círculo (2/4), esta expressão equivale a 1/2.
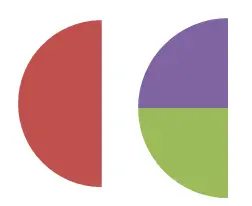
Nesta segunda imagem você pode ver a equivalência entre 1/2 e 2/4 , também pode ser verificada numericamente. Já que 1/2 = 0,5 e 2/4 = 0,5. Segundo a definição que comentamos anteriormente, se as duas frações expressam o mesmo valor numérico, então são frações equivalentes.
Exemplos de frações equivalentes
Mostraremos agora 5 exemplos de frações equivalentes. E se quiser entender como os calculamos, recomendamos que continue lendo.
- Frações equivalentes a meio: 2/4, 3/6, 4/8, etc.
- Frações equivalentes a um terço: 2/6, 3/9, 4/12, etc.
- Frações equivalentes a um quarto: 2/8, 3/12, 4/16, etc.
- Frações iguais à unidade: 4/4, 7/7, 15/15, etc.
- Frações equivalentes a um quinto: 2/10, 3/15, 4/20, etc.
Como calcular frações equivalentes?
Para obter frações equivalentes, precisamos multiplicar ou dividir o numerador e o denominador pelo mesmo número. Pois, se modificarmos as duas partes da fração da mesma forma, mantemos uma relação proporcional. Portanto, podemos utilizar dois métodos: amplificação e redução.
Encontrar uma fração equivalente por amplificação
Neste primeiro caso, precisamos multiplicar uma fração inicial por um determinado valor numérico. Isso significa que precisamos multiplicar o numerador e o denominador por esse número. Para que você possa ver com um exemplo, mostramos a seguir duas frações equivalentes, que são obtidas após fazer uma multiplicação:
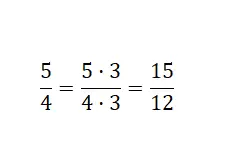
O que fizemos foi multiplicar ambas as partes da fração por três: 5 x 3 = 15 e 4 x 3 = 12 . Obtemos assim uma fração equivalente amplificada, pois é maior. Concluindo, encontramos uma fração composta por valores numéricos diferentes, que expressa a mesma quantidade da fração original.
Encontrando uma fração equivalente por simplificação
Em segundo lugar, podemos optar por simplificar uma fração dividindo o numerador e o denominador de uma determinada fração. Obteremos assim outra fração equivalente , ainda mais simples que a primeira. Porém, vale ressaltar que este método só funciona se a expressão inicial não for uma fração irredutível , uma vez que esta última não pode ser reduzida ainda mais. Abaixo está um exemplo de cálculo de uma fração equivalente por redução (simplificação).
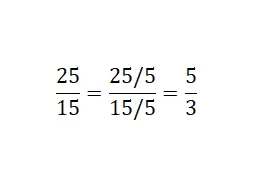
Como você pode ver na imagem, o que fizemos foi dividir o numerador e o denominador da fração por um divisor comum . Neste exemplo, usamos cinco: 25/5 = 5 e 15/5 = 3. Por fim, obtivemos a fração equivalente irredutível de 25/15.
Como você sabe se duas frações são equivalentes?
Para identificar frações equivalentes, devemos seguir um dos três procedimentos que explicaremos a seguir. Deve-se notar que o segundo está relacionado à simplificação de frações de que falamos na seção anterior.
Multiplicando numeradores por denominadores
Se quiser verificar a equivalência entre duas frações, você pode usar este primeiro procedimento. Basicamente, você tem que multiplicar o numerador da primeira fração pelo denominador da segunda. Em seguida, você precisa multiplicar o numerador da segunda fração pelo denominador da primeira. Se ambos os resultados fornecerem o mesmo , essas frações serão equivalentes. Veja o exemplo a seguir:
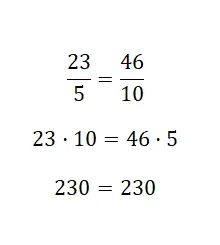
Neste último exemplo verificamos que as duas frações eram equivalentes. Este exemplo foi fácil de perceber, pois a segunda fração é o dobro da primeira, ou seja, possuem uma relação de equivalência ampliada . Ressalta-se que este procedimento é bastante confortável de usar, bastando apenas multiplicar as cruzes. Mas também recomendamos que você aprenda a usar os outros dois sistemas, pois isso lhe dará mais recursos matemáticos à sua disposição.
Simplifique frações
Quando se trata de frações não irredutíveis , podemos utilizar este outro método que consiste em reduzir ao máximo a fração composta pelos maiores números. Se, ao fazer esta redução, descobrirmos que a fração menor é a irredutível da outra, então podemos assumir que são equivalentes.
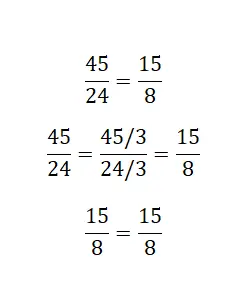
Resolver e equalizar divisões
Por fim, você pode recorrer à solução de quociente gerada por frações, pois um número misto é sempre uma divisão. Basicamente, você precisa calcular o valor numérico equivalente das duas frações e, se for o mesmo número, elas serão equivalentes. Na imagem a seguir você pode ver um exemplo muito claro:
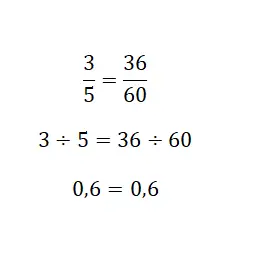
Exercícios sobre frações equivalentes
Agora que leu toda a teoria, pode tentar resolver os seguintes exercícios, que lhe permitirão terminar a compreensão da explicação. Recomendamos que você tente resolvê-los sozinho e, assim que os tiver, compare seu resultado com o que lhe oferecemos. Dito isto, deixamos você praticar:
Exercício 1
Encontre uma fração equivalente por simplificação para cada fração que oferecemos:
Para resolver este exercício basta aplicar a simplificação das frações, obtendo assim a fração irredutível equivalente. Os quatro exemplos são muito semelhantes, por isso não há muita dificuldade em resolvê-los.
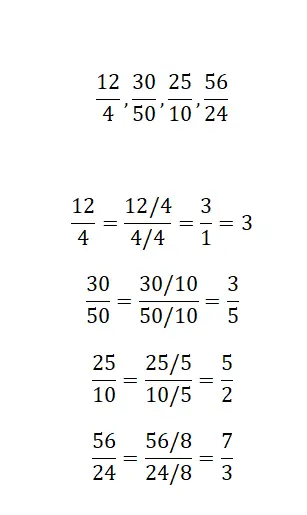
Exercício 2
Encontre uma fração equivalente por amplificação para cada fração que propomos:
A seguir terá que amplificar as frações que propomos, desta forma obterá frações equivalentes maiores. Não importa qual número você usa para fazer as multiplicações, por exemplo faremos com 2 e 3.
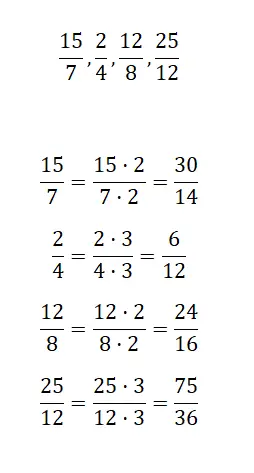
Exercício 3
Determine se as seguintes frações são equivalentes ou não:
Para descobrir se duas frações são equivalentes, você precisa usar um dos três métodos que explicamos acima. Você encontrará as correções resolvidas no primeiro procedimento, embora seja livre para usar o sistema que desejar.
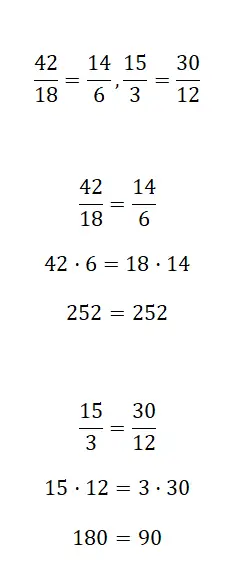
Exercício 4
Calcule as frações equivalentes das seguintes expressões:
Neste último exercício você terá que reescrever as expressões que propomos ( números inteiros e números mistos) em forma fracionária, tentando manter uma relação de equivalência.