Frações ou números mistos são expressões numéricas que indicam uma quantidade dividida por outra. É, portanto, um valor representado pelo quociente de dois números. Com este tipo de números podemos expressar quantidades decimais e inteiras e podemos até indicar proporções . A seguir definiremos as frações de uma forma mais matemática e mostraremos alguns exemplos, para que você entenda este conceito graficamente.
O que são frações?
Uma fração é igual ao número de partes que retiramos de uma unidade dividida em partes iguais. Então, graficamente, é representado por dois termos separados por uma linha horizontal no meio. Mais precisamente, no topo da linha encontramos o numerador e abaixo o denominador.
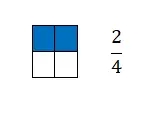
Como você pode ver, as frações são um conceito matemático muito fácil de representar graficamente porque andam de mãos dadas com proporções. É por isso que no exemplo anterior expressamos o número de quadrados coloridos com um número fracionário.
Termos fracionários
As duas partes da fração são:
- Numerador: Este termo está localizado acima da linha horizontal e é aqui que escrevemos a quantidade de peças que pegamos. Podemos encontrar numeradores positivos, negativos e zero (igual a zero).
- Denominador: Este outro termo está localizado abaixo da linha e é aqui que escrevemos o número total de partes em que a unidade está dividida. Podemos encontrar denominadores positivos e negativos, mas estes não podem ser zero.
tipos de frações
Existem muitos tipos de frações, dependendo dos números que as compõem e da equivalência que apresentam com outras frações. A seguir definiremos todas as categorias existentes e comentaremos as características que permitem diferenciá-las das demais:
- Frações próprias: são aquelas formadas por um numerador menor que o denominador. Se você converter essas frações em decimal , obterá um número entre zero e um. Não pode ser maior que um, pois o valor do numerador será sempre menor que o do denominador e, portanto, a unidade não será ultrapassada.
- Frações impróprias: são aquelas que possuem numerador maior que o denominador, neste caso expressam valores numéricos maiores que a unidade. Como por exemplo, 8/5 é igual a 1,6 que é maior que 1. Esta é outra forma de expressar números mistos, que são do seguinte tipo.
- Frações mistas: também chamadas de números mistos, são aquelas compostas por um número inteiro e um número misto. Basicamente eles são representados com o valor inteiro antes da fração, então para convertê-los em frações impróprias é necessário multiplicar a parte inteira pelo denominador, somar ao numerador e deixar o denominador igual.
- Frações decimais: são aquelas que possuem um denominador que expressa uma quantidade equivalente a uma potência de dez, por exemplo: 6/10, 34/1000 ou 5/100. Eles são usados em notação decimal e são mais comuns na conversão de números decimais exatos em números mistos. Discutiremos isso com mais detalhes na próxima seção.
- Frações compostas: são aquelas que são compostas por outra fração, seja no numerador, seja no denominador, ou em ambos. Então, para simplificar estas expressões e representá-las como uma única fração, precisamos dividir o numerador pelo denominador. Isto ficará mais claro quando explicarmos a divisão entre frações.
- Frações equivalentes: são aquelas que equivalem ao mesmo número, embora não sejam constituídas pelos mesmos numeradores ou denominadores. Por exemplo, 8/4 = 4/2 = 2, ambas as frações são iguais a dois. Neste caso específico é porque a primeira fração é igual ao dobro da segunda, portanto, mantém uma relação proporcional.
- Frações irredutíveis: São aquelas que não podem ser mais simplificadas, pois o numerador e o denominador não compartilham fatores comuns e, portanto, não podem ser divididos por nenhum número. Alguns exemplos desse tipo são: 9/5, 5/6, 7/8, entre outros. Para saber detectá-los é importante saber calcular o máximo divisor comum .
Operações com frações
Agora que conhecemos as diferentes categorias de frações existentes, veremos como resolver as diferentes operações aritméticas com números mistos . Deve-se destacar que isso é um pouco mais complicado do que operações com números inteiros, embora depois de entender a metodologia tudo seja bastante fácil. Além disso, não apenas explicaremos a teoria, mas também mostraremos alguns exemplos. Dito isso, vamos começar.
soma de frações
Somar frações com denominador comum é bastante simples, bastando somar os dois numeradores e deixar o denominador igual. Por outro lado, somar frações com denominadores diferentes é um pouco complicado, porque é preciso encontrar o menor múltiplo comum dos denominadores. E então, devemos somar o produto de cada numerador dividindo o lcm (o novo denominador) pelo antigo denominador. Para entender melhor, você pode observar o seguinte diagrama:
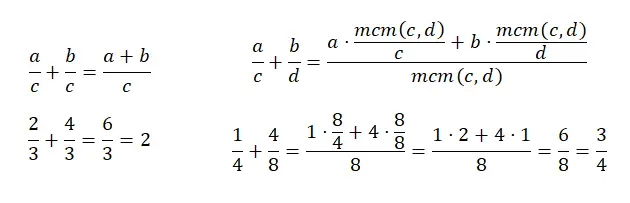
frações de subtração
A subtração de frações com denominador comum é muito parecida com a adição, na verdade tudo é feito da mesma forma exceto na soma dos numeradores, porque em vez de somar é preciso subtrair. E na subtração de frações com denominadores diferentes acontece a mesma coisa, é praticamente a mesma coisa só que ao invés de somar o produto dos numeradores dividindo o mcm pelo denominador antigo, devemos subtrair. Aqui está outro diagrama:
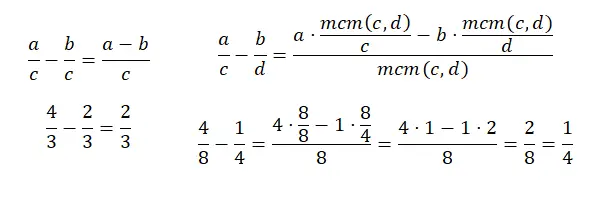
multiplicação de frações
A multiplicação de frações pode ser resolvida da mesma maneira, sejam os denominadores iguais ou não. Basicamente, você tem que multiplicar os numeradores por uma parte e os denominadores por outra. Esta é talvez a operação mais simples, pois basta realizar duas multiplicações.
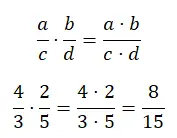
divisão de frações
Dividir em frações também é bastante fácil de resolver, basta multiplicar as cruzes. Em outras palavras, o numerador é o resultado da multiplicação do numerador da primeira fração pelo denominador da segunda. enquanto o denominador é o produto do denominador da primeira fração e do numerador da segunda.
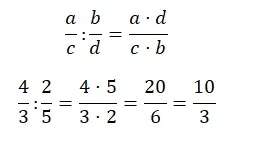
Simplifique frações
Simplificar frações ou reduzir frações não é uma operação aritmética propriamente dita, mas é muito importante saber como fazê-lo e também, é um tema que já abordamos um pouco com os tipos de frações. Portanto, para simplificar um número misto, precisamos dividir o numerador e o denominador pelo mesmo número. Geralmente, escolheremos o máximo divisor comum para fazer esta simplificação. Na imagem a seguir você pode encontrar um exemplo.
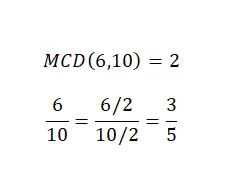
Como você pode ver, temos duas frações equivalentes , portanto ambas representam o mesmo valor numérico, mas a segunda é mais simples que a primeira. Portanto, atingimos com sucesso o objectivo de simplificação.
Como passar de decimal para fração e vice-versa?
A fração geradora é a fração irredutível obtida de um número decimal, seja um número decimal exato ou um número decimal repetido. Claro, precisaremos usar métodos diferentes dependendo do tipo de decimal, que discutiremos a seguir.
Converter de decimal exato em fração geradora
Neste caso podemos recorrer às frações decimais que comentamos no início. Simplesmente, precisamos escrever o valor numérico no numerador, mas sem a vírgula. Enquanto no denominador escrevemos a potência de dez que tem tantos zeros quantos algarismos no numerador.
No entanto, se tivermos um número decimal maior que um, como 4,25, precisaremos multiplicar o número de unidades completas que temos pelo valor do denominador e adicioná-lo ao numerador original. Abaixo você encontrará um exemplo de cada tipo:
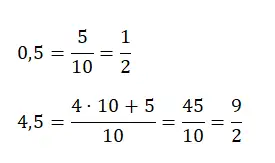
Converter decimal repetido puro em fração geradora
Quando temos um número decimal periódico puro , se quisermos obter a fração geradora, teremos que colocar o mesmo valor no numerador, mas sem vírgula e subtrair a parte inteira. Embora o denominador seja igual a um número composto apenas por noves, devemos escrever especificamente tantos noves quanto o número de dígitos na parte decimal do número original. Este sistema é um tanto confuso, mas com alguns exemplos vamos entender:
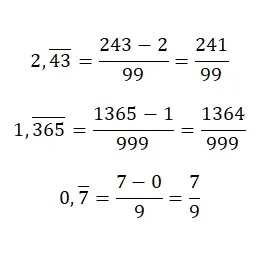
Converter decimais repetidos mistos em frações geradoras
No caso de termos um número decimal repetido misto , teremos que aplicar uma regra bastante complexa. Primeiramente, escreveremos o número sem vírgula no numerador e subtrairemos a parte inteira seguida das dízimas não recorrentes, também sem vírgula. Quanto ao denominador, você precisará escrever tantos noves quantos os dígitos da parte decimal periódica, seguidos de tantos zeros quantos os dígitos da parte decimal não recorrente.
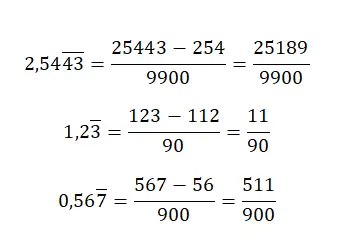
converter fração em decimal
Para passar de uma fração para um decimal, basta dividir o numerador pelo denominador, pois um número misto nada mais é do que o quociente entre dois valores . Assim, ao resolver a divisão, você obtém o número decimal correspondente. Na imagem a seguir você pode encontrar alguns exemplos bastante simples:
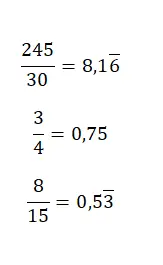
exercícios de frações
Agora que você conhece toda a teoria sobre frações, recomendamos que faça alguns exercícios. Assim você aprenderá todos os conceitos explicados com mais profundidade e no dia do exame você terá mais rapidez na resolução dos cálculos. Além disso, você terá visto todos os tipos deexercícios de frações existentes e saberá como resolvê-los adequadamente. Por fim, deixe-me dizer que também temos à sua disposição uma calculadora de frações online, com a qual você pode resolver todas as operações com frações.