Uma equação quadrática ou equação quadrática é uma equação de grau 2, com a qual o maior expoente de um de seus termos é igual a 2. Isso significa que a equação pode ter até duas soluções diferentes, embora também possa ter uma solução única ou Nenhum mesmo.
Para calcular as soluções ou raízes das equações quadráticas, podemos seguir dois procedimentos diferentes: por meio da fórmula quadrática ou pela fatoração da expressão . Neste artigo falaremos sobre os dois métodos e daremos alguns exercícios práticos. Porém antes vamos esclarecer alguns conceitos para que toda a explicação seja muito bem compreendida e você aproveite ao máximo a leitura.
Tipos de equações quadráticas
A principal categorização entre equações quadráticas é baseada na estrutura da própria expressão. Assim, a estrutura padrão ou usual destas expressões é a seguinte: ax² + bx + c . Essa forma comum é equivalente a uma equação completa, mas quando há termos nulos ou nulos, a estrutura pode variar, e é aí que aparecem as equações incompletas. A seguir explicaremos com mais detalhes as características de todos os tipos.
Equações quadráticas completas
Como já dissemos, temos as equações quadráticas completas , estas possuem todos os coeficientes a, b e c diferentes de zero. A expressão segue, portanto, ao pé da letra a estrutura ax² + bx + c, pois possui todos os termos: o termo quadrático, o termo linear e o termo independente. Um exemplo desse tipo é a seguinte equação: x² + 2x + 1 = 0.
Equações quadráticas incompletas
Quanto às equações incompletas, podemos distingui-las de acordo com o coeficiente igual a zero. Lembre-se que se esta explicação não tirar suas dúvidas, logo abaixo está uma imagem na qual você encontra todos os casos explicados passo a passo.
- Equações incompletas (b = 0): nesta primeira situação encontramos uma expressão que segue a seguinte estrutura: ax² + c = 0. Com a qual obtemos dois resultados: o negativo e o positivo da raiz da fração c/a .
- Equações incompletas (c = 0): quando temos a forma ax² + bx = 0 devemos fatorar a equação para ter a expressão x (ax + b) = 0. Teremos portanto duas soluções: x = 0 e x = – BA.
- Equações incompletas (b = c = 0): neste caso temos uma equação ax² = 0 e só temos uma solução possível, que é x = 0.
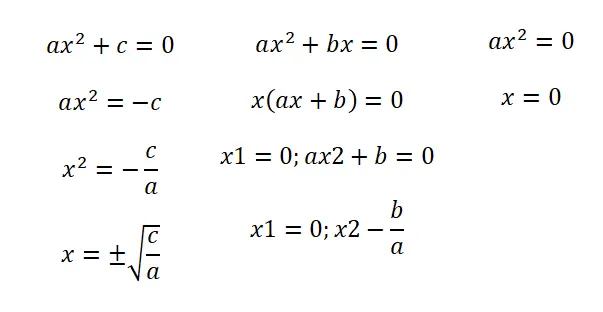
Vale ressaltar que os procedimentos que ensinamos permitem que você seja mais rápido na resolução de equações incompletas. Mas, em todos os casos você pode usar a fórmula quadrática que ensinaremos a seguir, bastando escrever zero nos coeficientes que não existem.
Fórmula para equações quadráticas
Para resolver equações quadráticas (ax² + bx + c = 0), precisamos aplicar a fórmula geral ou fórmula quadrática e depois precisamos substituir os valores numéricos que correspondem a cada letra da expressão matemática.
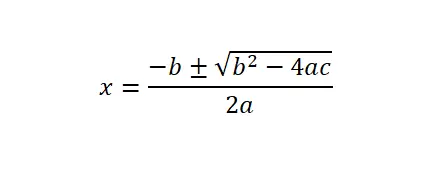
Além disso, é importante explicar que o discriminante (Δ) é a expressão b² – 4ac, que está localizada abaixo da raiz quadrada. A partir deste conceito matemático podemos saber quantas soluções esta equação quadrática possui. Basicamente, existem três opções: o discriminante é negativo (não existem soluções reais), o discriminante é zero (existe apenas uma solução) ou o discriminante é positivo (existem duas soluções).
Exemplo de uma equação quadrática completa resolvida
Tente resolver a seguinte equação quadrática: 2x²+4x-6=0 e compare seu resultado com o abaixo. Recomendamos que você siga o seguinte procedimento: analise o tipo de equação (identifique os termos zero), calcule o discriminante para saber a quantidade de soluções existentes e por fim, resolva a equação proposta com a fórmula.
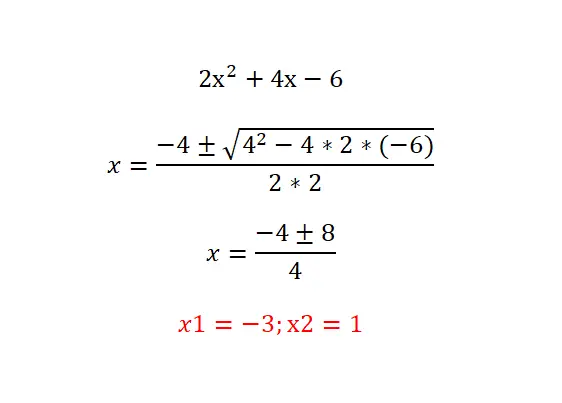
Equações quadráticas fatoriais
O segundo método que temos para resolver equações quadráticas é a fatoração . Portanto, para fatorar um polinômio (no nosso caso, um polinômio quadrático), podemos usar diferentes métodos. Embora em geral, quando se trata de equações deste estilo, elas geralmente são fatoráveis por um termo comum. E se não, você pode tentar aplicar Notable Identities , mas normalmente não precisará conhecer nenhum outro método nessas situações.
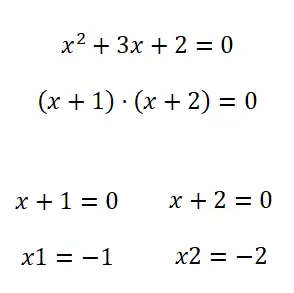
Exercícios de equações quadráticas com soluções
Abaixo você encontrará uma série de exercícios sobre equações quadráticas completas e incompletas . Assim você revisará toda a teoria explicada ao longo deste artigo e ficará mais claro como aplicá-la nos exercícios. Recomendamos que você tente resolvê-los sozinho e só veja a solução quando tiver concluído ou quando tiver dúvidas. Dito isto, você pode começar a resolver os exercícios agora.
Exercício 1
Resolva a seguinte equação quadrática:
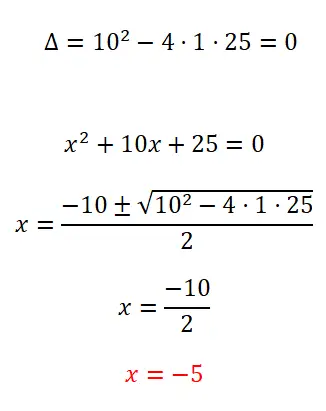
- Começamos calculando o discriminante, para saber o número de soluções possíveis.
- Como esta é uma equação quadrática completa, aplicamos a fórmula quadrática e resolvemos os cálculos.
- Obtemos o valor da incógnita x.
Exercício 2
Resolva a seguinte equação quadrática:
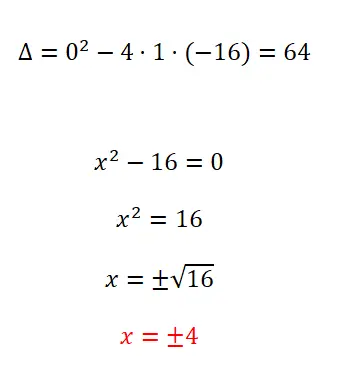
- Começamos calculando o discriminante.
- Como temos uma equação quadrática incompleta em que b = 0, aplicamos o padrão para equações deste tipo.
- Resolvemos o cálculo para obter o resultado, e não podemos esquecer do sinal ±.
Exercício 3
Resolva a seguinte equação quadrática não ordenada:
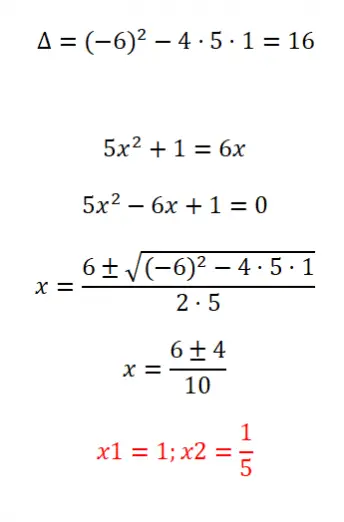
- Começamos calculando o discriminante da equação.
- Antes de podermos aplicar a fórmula, precisamos ordenar a equação de acordo com a estrutura ax² + bx + c = 0.
- Então aplicamos a fórmula geral.
- E finalmente obtemos os resultados.
Exercício 4
Resolva a seguinte equação quadrática fatorando:
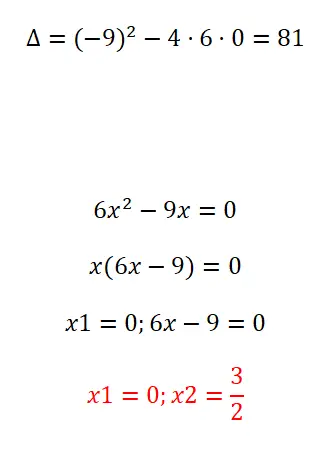
- Primeiro calculamos o discriminante.
- A seguir, extraímos o fator comum de x.
- Portanto, a primeira solução é x = 0.
- E o segundo é x = 3/2.
Exercício 5
Resolva a equação quadrática completa que mostramos abaixo:
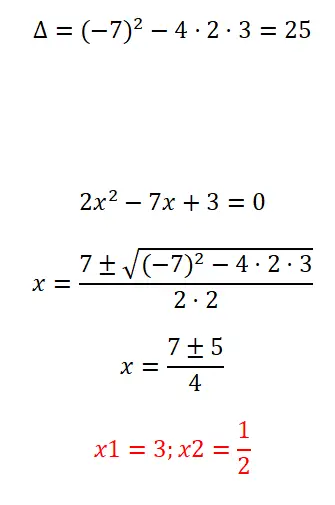
- Como sempre, calculamos o discriminante para descobrir quantas soluções a equação em questão possui.
- A seguir, aplicamos a fórmula quadrática, por se tratar de uma equação completa.
- Finalmente, expressamos o resultado da equação.
Exercício 6
Resolva a equação quadrática com frações que oferecemos:
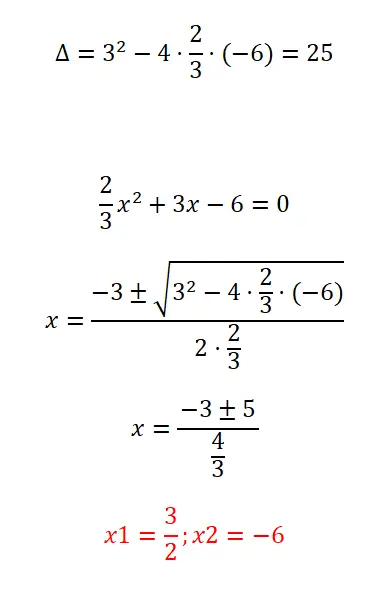
- Começamos calculando o discriminante da expressão.
- A seguir aplicamos a fórmula quadrática, levando em consideração que o coeficiente “a” é formado por uma fração.
- Resolvemos o cálculo.
- E já temos as duas raízes da equação.
Exercício 7
Resolva a seguinte equação quadrática:
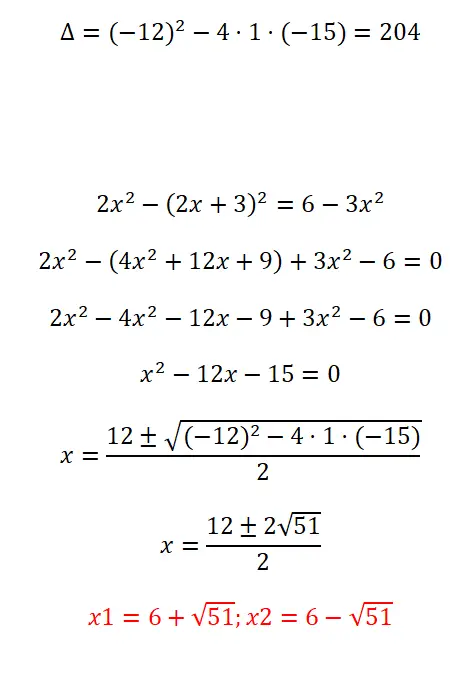
- Começamos calculando o discriminante.
- Antes de aplicar a fórmula, precisamos simplificar a expressão e dar-lhe a forma ax² + b + c = 0.
- Substituímos todos os coeficientes na fórmula e resolvemos o cálculo.
- Finalmente obtemos o resultado.
Exercício 8
Prova de resolução da seguinte equação quadrática:
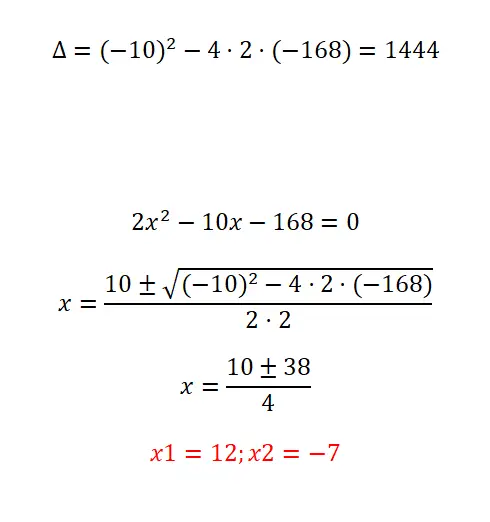
- Começamos calculando o discriminante.
- Como você pode ver, esta é uma equação quadrática simples, embora tenha coeficientes bastante grandes. Portanto, precisamos aplicar a fórmula e ter cuidado ao realizar as operações.
- No final, obtemos as duas soluções possíveis.