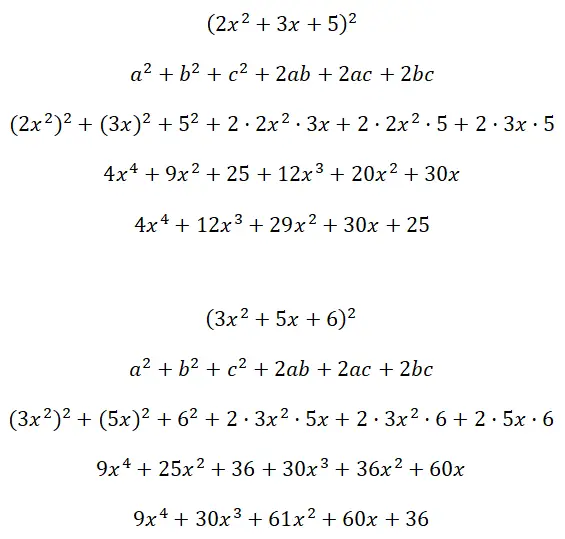Que sont les produits remarquables ou les identités remarquables ?
Les identités remarquables , également appelées produits remarquables ou égalités remarquables , sont des ressources mathématiques qui permettent de résoudre plus rapidement des produits et des quotients de polynômes . Comme le mot identité l’indique, ce sont des égalités qui nous permettent de calculer ces opérations sans avoir à les résoudre. Puisque nous savons que cette expression suit des règles fixes (qui sont toujours remplies) et, par conséquent, nous pouvons obtenir le résultat sans avoir à le vérifier.
Quand utiliser une identité notable ?
Ces identités sont principalement utilisées dans le domaine de l’algèbre et leur fonction principale est d’accélérer la résolution d’un certain polynôme, sans avoir à résoudre toute l’opération elle-même. De là, on obtient les formules des produits notables, que nous commenterons tout au long de l’article. Et enfin, on peut appliquer les formules pour faire la complétion de carrés, la factorisation de polynômes ou tout autre type de calcul.
Comment résoudre un produit remarquable étape par étape ?
Afin de résoudre des identités notables, vous devez suivre une procédure très simple, qui est également très logique :
- Identifier le type d’identité notable : La première étape consiste à identifier le type d’opération : un produit notable ou un quotient notable. Vous devez également préciser quel type de formule vous devrez appliquer, même si vous le comprendrez plus tard, une fois que nous aurons expliqué les différents types d’identités notables.
- Appliquez la formule : une fois que vous savez quelle formule vous devez appliquer, il est temps de faire les calculs. Selon le type d’identité, vous aurez à résoudre des opérations plus ou moins complexes et dans la grande majorité des cas, ces calculs seront constitués de termes qui contiennent au moins une inconnue.
- Simplifiez l’expression : Enfin, lorsque vous obtenez le résultat, vous devez le simplifier. Dans cette étape, vous devez regrouper des termes similaires et les ordonner pour former un polynôme résultant bien structuré. Il est à noter que cette étape est tout aussi importante que les autres, car sinon, l’exercice reste inachevé.
Formules des identités notables ou principaux produits notables
Ci-dessous, vous trouverez toutes les formules correspondant aux identités notables. En plus de l’explication théorique de chaque cas, il y a aussi quelques exemples de produits notables résolus, grâce auxquels vous comprendrez mieux tous les concepts. Il convient de mentionner que dans cette première section, vous ne trouverez que les identités les plus importantes . Mais, en lisant cet article, vous apprendrez à développer des produits notables plus complexes, comme ceux constitués de trinômes.
carré d’une somme
Le premier cas concerne le carré de la somme , qui est une expression polynomiale très courante dans le monde de l’algèbre. Cela peut être trouvé écrit comme suit : (a + b) 2 , ce qui équivaut à : (a + b) · (a + b). Par conséquent, nous savons qu’il peut être résolu au moyen d’une multiplication de polynômes. Mais, grâce aux identités notables, on peut gagner du temps en utilisant la formule suivante : (a + b) 2 = a 2 + 2ab + b 2 . Ensuite, nous vous montrons la démonstration de la formule que nous venons de voir, de cette façon, vous pourrez comprendre d’où elle vient et comment elle est utilisée :
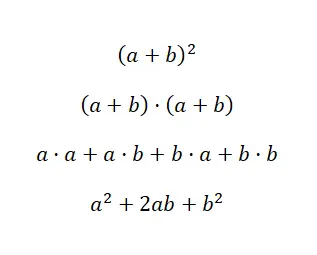
Comme on peut le voir, nous avons fait la vérification à partir de la multiplication des polynômes que nous avons précédemment commentée. Et nous pouvons affirmer avec une certitude absolue que si vous connaissez par cœur la formule résultante, alors en effectuant une simple substitution de valeurs , vous pouvez obtenir le résultat plus rapidement. C’est donc un concept mathématique très utile. Maintenant que vous savez comment fonctionne le carré d’une somme, nous allons vous montrer un exemple concret :
Exemple du carré d’une somme
Calculer l’identité notable (2x + 4) 2 :
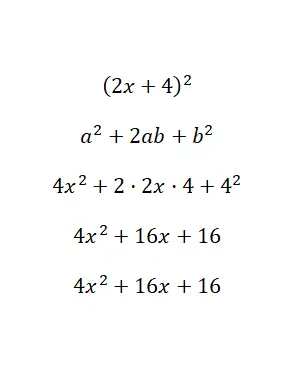
Fondamentalement, nous avons associé les valeurs du binôme aux lettres de la formule et nous avons résolu : a = 2x et b = 4. Enfin, après avoir résolu tous les calculs, nous obtenons le polynôme 4x 2 + 16x + 16, qui est équivalent à l’original . Dans cet exemple, nous avons obtenu un polynôme développé (sous forme standard) à partir d’un polynôme réduit.
carré d’une soustraction
Une autre expression très courante est le carré de la soustraction , qui ressemble beaucoup au carré d’une addition, il change simplement d’un signe. Alors, la structure du binôme est équivalente à : (a – b) 2 , et si on la déplie on obtient : (a – b) · (a – b). Comme dans le cas précédent, celui-ci peut être calculé à partir d’une multiplication de polynômes, bien qu’il ait également une formule qui facilite la résolution : a 2 – 2ab +b 2 . Ci-dessous, vous pouvez trouver la preuve empirique de ceci :
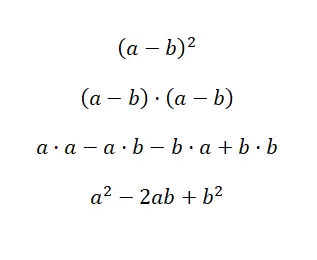
Pour simplifier la résolution du carré d’une différence, nous pouvons utiliser la même formule que celle que nous avons utilisée pour la somme d’un carré, mais avec le premier signe négatif . Ce changement minimal permet d’adapter l’expression aux binômes composés d’un terme positif et d’un terme négatif, ce qui est utile pour les soustractions. Nous allons maintenant vous montrer un exemple résolu :
Exemple du carré d’une soustraction
Calculer l’identité notable (x – 3) 2 :
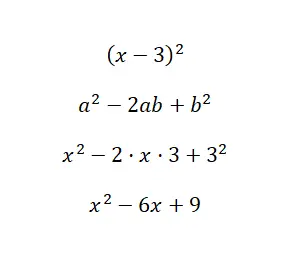
Comme vous pouvez le voir dans l’exemple de solution, nous avons substitué les valeurs de notre binôme dans la formule, a = x et b = 3. Par conséquent, en utilisant la formule que nous avons expliquée précédemment, nous n’avons eu qu’à faire la substitution et quelques calculs très basiques. Cela nous permet de voir avec quelle facilité le carré d’une différence peut être calculé avec cette expression.
Différence des carrés ou somme par différence
Le troisième cas de produits notables est appelé la différence des carrés , celle-ci est formée par le produit d’un binôme positif et d’un binôme négatif. Une expression de ce style a la structure suivante : (a + b) · (a – b), donc si nous développons ce produit nous obtenons la formule qui facilite le calcul : a 2 – b 2 . Comme vous pouvez le voir, c’est une formule très simple, même si pour bien la comprendre il faut développer tous les calculs :
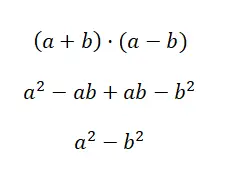
Exemple de somme par différence
Calculer l’identité notable (x + 1) · (x – 4) :
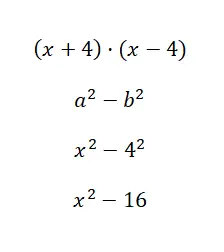
A cette occasion, le calcul numérique est très facile, en effet nous n’avons eu qu’à résoudre une puissance. Bien qu’il soit vrai que cette formule n’est applicable que lorsque les binômes ont le même terme principal et le même terme indépendant, mais avec un signe changé. Donc cette identité est importante, mais ce n’est pas celle que vous allez le plus utiliser.
Produit de deux binômes avec un terme commun
Dans ce quatrième cas, on se trouve devant une situation très similaire à la précédente, bien qu’avec une légère modification dans la structure. Observez la différence que nous vous montrons : (x + a) · (x + b) et (a + b) · (a – b). Au cas où vous ne le voyez toujours pas très clairement, considérez l’exemple suivant : (x + 4) · (x + 5) et (x + 4) · (x – 4). Dans le premier cas (le produit de deux binômes de terme commun ) il n’y a qu’un seul terme partagé, tandis que dans le second cas (la somme par différence) les deux termes sont communs, mais le terme indépendant a son signe inversé. Cela dit, voyons avec quelle formule nous pouvons agir :
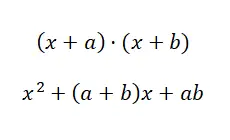
Exemple du produit de deux binômes avec un terme commun
Résolvez le produit notable (x + 2) · (x + 3) :
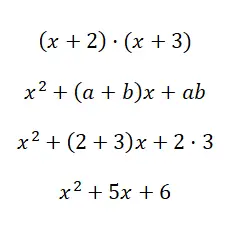
En utilisant la formule de x 2 + (a + b)x + ab nous pouvons calculer le polynôme du second degré résultant de la multiplication des deux binômes. Nous espérons que grâce à cet exemple, vous avez compris la différence entre les deux derniers cas que nous avons expliqués, car il peut parfois être difficile de les distinguer.
carré d’un trinôme
Lorsque nous essayons de calculer le carré d’un trinôme, nous avons également un produit remarquable qui nous facilite la vie. Cette expression est représentée comme ceci : (a + b + c) 2 et le produit équivalent est : a 2 + b 2 + c 2 + 2ab + 2ac + 2bc. Il convient de noter que cela est valable dans le cas d’un trinôme positif, mais si l’un des coefficients est négatif, il vous suffit d’écrire la valeur négative dans la formule. Vous trouverez ci-dessous la démonstration de la formule :
Exemple du carré d’un trinôme
Calculer l’identité notable (2x + 1 + x 2 ) 2 :
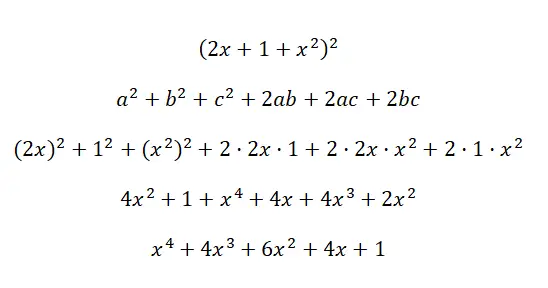
Formules d’identités remarquables ou produits remarquables cubés
Maintenant que nous avons expliqué les principales identités notables, nous allons voir leurs dérivées , en commençant par les binômes au cube. Pour calculer des produits notables de ce style, nous devrons recourir à des formules un peu plus complexes, mais qui suivent une structure similaire à celles dont nous avons déjà parlé.
binôme au cube
Le cube d’un binôme s’écrit : (a + b) 3 et (a – b) 3 , cette expression est équivalente à la formule suivante : (a 3 + 3a 2 b + 3ab 2 + b 3 ), et (a 3 – 3a 2 b + 3ab 2 – b 3 ). Ces deux cas sont appelés cube d’une somme et cube d’une soustraction, car ce sont des binômes au cube. Ci-dessous, vous trouverez une démonstration très détaillée de chaque cas :
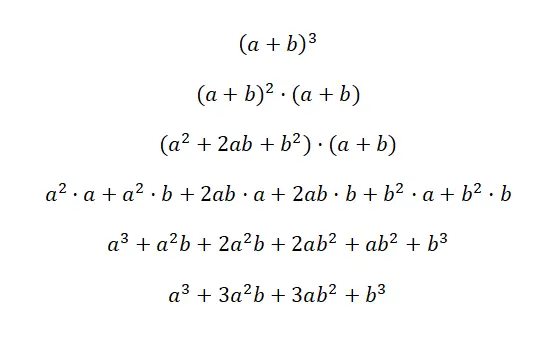
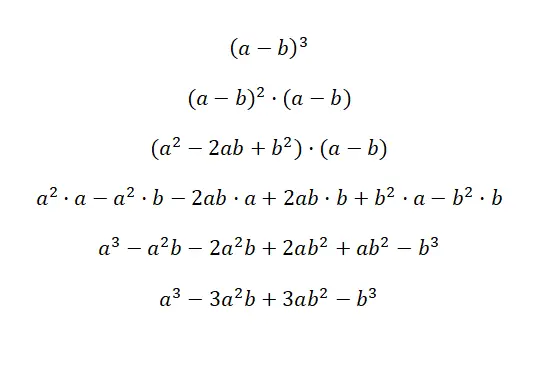
La clé pour comprendre cette première preuve est de comprendre que (a + b) 3 est équivalent à : (a + b) 2 · (a + b). De cette manière, nous utilisons la formule du carré d’une somme , que nous avons expliquée précédemment pour multiplier l’autre facteur. Ensuite on simplifie simplement l’expression, et on obtient l’identité notable correspondante : a 3 + 3a 2 b + 3ab 2 + b 3 . Dans le cas du deuxième exemple, la même chose se produit, mais avec un changement de signe.
Exemple du cube d’un binôme
Résoudre l’identité notable (x + 3) 3 :
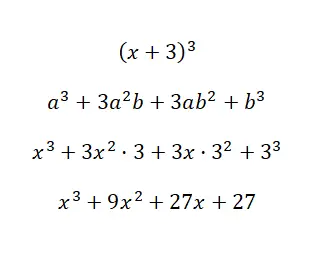
En utilisant la formule dont nous venons de discuter, nous pouvons calculer le polynôme, en tenant compte du fait que : a = xyb = 3. Comme vous pouvez le voir, la procédure est très simple et n’a pas beaucoup de complications dans le calcul, c’est parce que nous avons la formule. Sinon, devoir faire une multiplication tant que cela serait assez fastidieux.
Somme de cubes et différence de cubes
Nous avons aussi cet autre cas, qui peut être facilement confondu avec le précédent. Bien que les deux cas soient écrits de manière différente, ils ne sont pas équivalents. L’expression équivalente à la somme ou la différence des cubes est : a 3 + b 3 , alors que dans le cas précédent on parlait de : (a + b) 3 . Comme vous pouvez le voir, il y a une similitude indéniable dans la structure de l’expression, mais en réalité, lorsqu’il s’agit de développer le calcul, ce sont deux cas totalement différents :
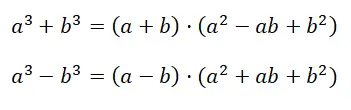
Dans la démonstration de la formule on obtient la factorisation du premier polynôme , précisément on passe du binôme initial au produit d’un binôme par un trinôme. Il semble que le résultat obtenu (a + b) · (a 2 – ab + b 2 ), ne simplifie pas du tout le calcul, mais en réalité, en factorisant le polynôme on obtient une expression très facile à comprendre.
Exemple de somme de cubes
Calculez le produit notable x 3 + 27 :
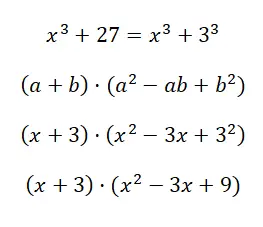
Dans ce cas, le résultat que nous obtenons est assez long, car il ne peut pas être simplifié davantage. Mais, il est normal d’arriver à cette expression, en effet, dans ces cas vous ne pouvez obtenir qu’un résultat avec la structure équivalente au produit d’un binôme par un trinôme, comme dans cet exemple.
trinôme au cube
Le cube d’un trinôme s’écrit : (a + b + c) 3 , ce qui revient à multiplier trois trinômes identiques, mais sans exposant : (a + b + c) · (a + b + c) · (a + b + c). C’est le produit notable le plus complexe qui soit, bien que la formule soit assez logique et s’obtienne de la même manière que tous, lorsque vous effectuez les multiplications correspondantes de polynômes. Ci-dessous, vous trouverez la preuve de la formule de cette identité remarquable :
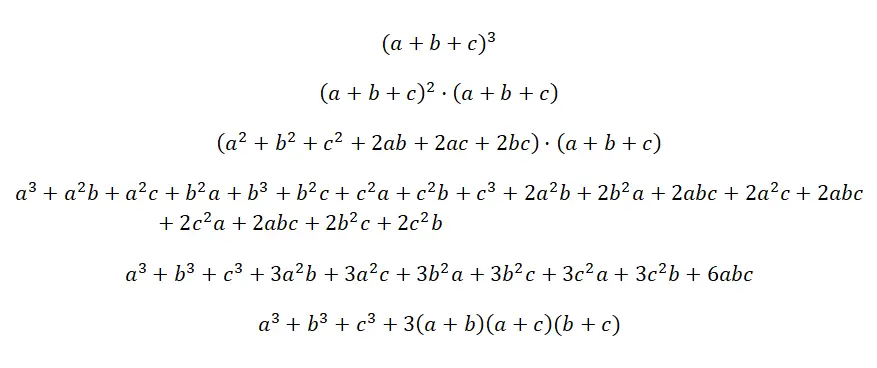
Exemple du cube d’un trinôme
Résolvez le cube trinôme suivant (x 2 + 3x – 4) 3 :
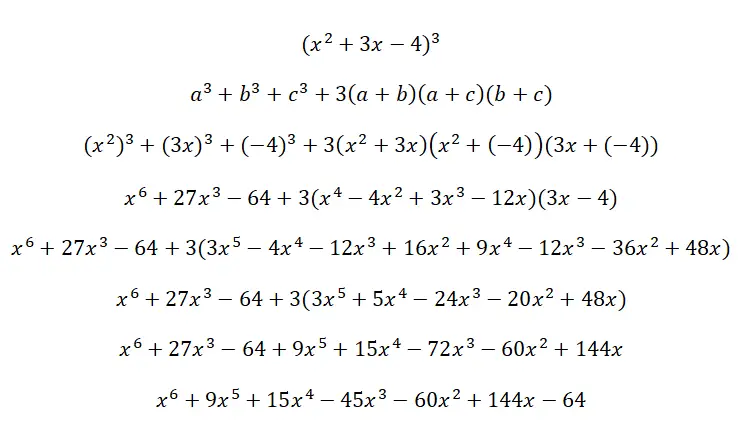
des ratios remarquables
Enfin, nous expliquerons les quotients notables , qui sont des identités notables permettant de résoudre rapidement certains types de fractions algébriques. Plus précisément, il existe quatre types différents, qui partagent une caractéristique : leur résultat est formé de polynômes exacts (avec un reste égal à zéro). Il convient également de mentionner que les formules des quotients remarquables ont une certaine relation avec les formules des produits remarquables que nous avons déjà expliquées.
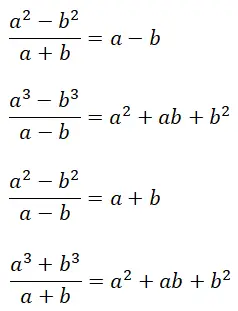
Exemple de ratios remarquables résolus
Calculez les ratios notables suivants :
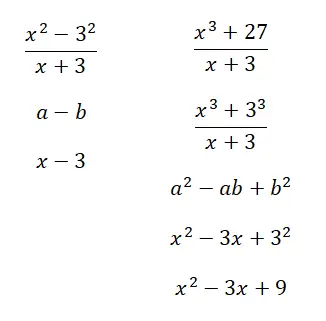
Exercices de produits remarquables résolus
Maintenant que vous savez comment les différents notables sont résolus, il est temps pour vous de vous entraîner un peu. C’est pourquoi nous vous proposons 6 exercices pour appliquer toute la théorie expliquée. Et nous vous montrons un tableau des principales identités notables, afin que vous l’ayez sous la main pendant que vous résolvez tous les exercices :

Exercice 1
Résolvez les carrés binomiaux (x – 4) 2 , (x + 1) 2 et (x – 3) 2 :
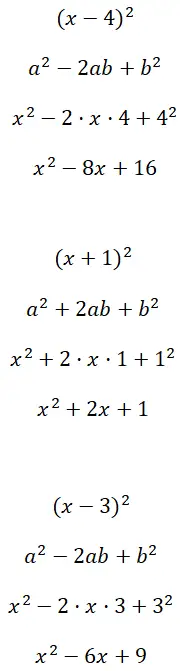
Exercice 2
Calculer les deux différences de carrés (x – 1) · (x + 1) et (x + 3) · (x – 3) :
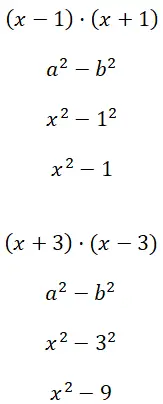
Exercice 3
Développer les produits notables au cube (x – 5) 3 et (x + 8) 3 :
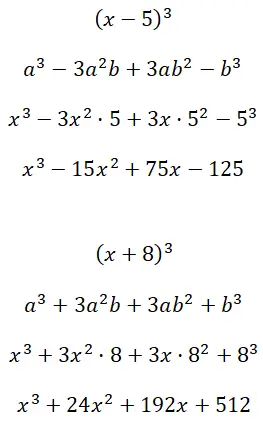
Exercice 4
Développer des identités notables formées de termes à plusieurs facteurs (4x 2 + 5y) 2 , (5x 3 + y 2 ) · (5x 3 – y 2 ) et (5xy 2 – 2xy) 2 :
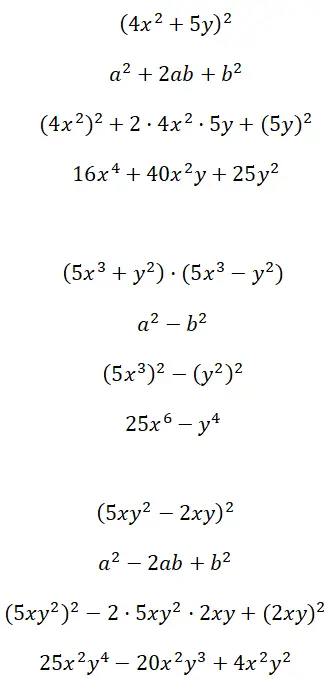
Exercice 5
Calculer les produits cubiques notables formés par les termes à plusieurs facteurs (3x 2 + y) 3 et (5y 3 – 2x 2 ) 3 :
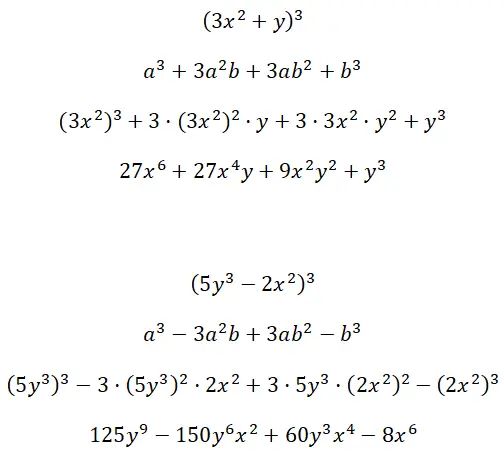
Exercice 6
Résolvez les carrés des trinômes (2x 2 + 3x + 5) 2 et (3x 2 + 5x + 6) :