▷ Calculer le produit vectoriel de deux vecteurs (exemples)

Cette page explique ce qu’est le produit vectoriel de deux vecteurs et comment il est calculé. Vous verrez également comment connaître la direction et le sens du produit vectoriel à l’aide de la règle de la main droite (ou du tire-bouchon). Et en plus, vous trouverez les utilisations de ce type d’opération, ainsi que des exemples, des exercices et des problèmes résolus étape par étape.

Quel est le produit vectoriel de deux vecteurs ?

En mathématiques, le produit vectoriel est une opération entre deux vecteurs dans un espace tridimensionnel (dans R3). Le résultat de cette opération vectorielle est un vecteur de direction perpendiculaire aux deux vecteurs multipliés, et de module égal au produit des modules des vecteurs multiplicateurs par le sinus de l’angle qu’ils forment. Autrement dit, sa formule est :

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

Comme vous le voyez dans la formule précédente, le produit vectoriel est noté

$\bm{\times}$ , c’est pourquoi on l’appelle aussi produit croisé. On l’appelle aussi parfois le produit vectoriel de Gibbs, puisque c’est lui qui l’a inventé.

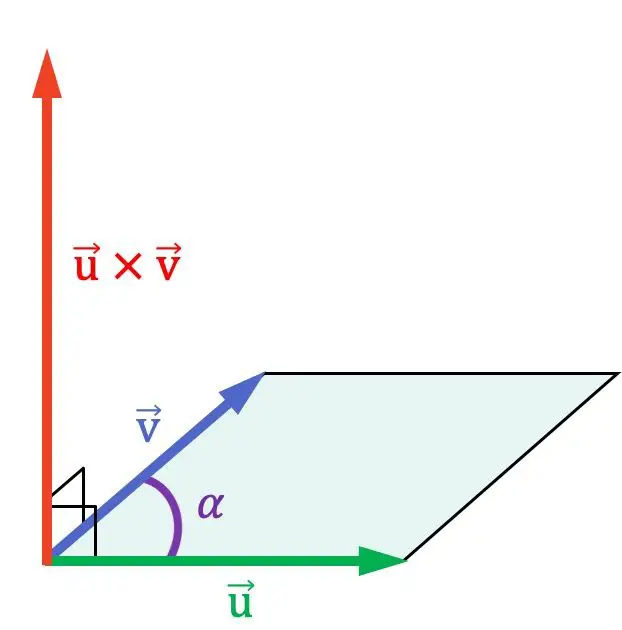
Comme vous pouvez le voir dans la représentation graphique précédente, le produit vectoriel est perpendiculaire aux deux vecteurs qu’ils multiplient et, par conséquent, il est normal au plan qui les contient.

Formule pour calculer le produit vectoriel de deux vecteurs

Si nous connaissons les coordonnées cartésiennes des vecteurs, le moyen le plus simple de calculer leur produit vectoriel est de résoudre un déterminant 3×3. Regardez comment c’est fait :

Soit deux vecteurs quelconques :

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Son produit vectoriel est :

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

Où les vecteurs

$\vv{i}, \vv{j},\vv{k}$ Ce sont les vecteurs unitaires dans les directions des axes X, Y et Z respectivement.

Voyons un exemple de la façon de calculer le produit vectoriel entre deux vecteurs :

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

Pour déterminer le produit vectoriel entre les vecteurs, il faut faire le déterminant d’ordre 3 suivant :

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

Dans ce cas, nous résoudrons le déterminant par adjuvants ou cofacteurs (la règle de Sarrus pourrait également être utilisée) :

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

Le résultat du produit vectoriel des deux vecteurs est donc :

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

Déterminer la direction et le sens du produit vectoriel

Parfois on n’a pas besoin de connaître les composantes du vecteur résultant du produit vectoriel, mais il suffit de trouver son module, son sens et sa direction. Cela arrive souvent en physique, notamment dans le calcul des forces.

Ainsi, il existe plusieurs règles pour trouver la direction et le sens du produit vectoriel, les plus connues sont la règle de la main droite , soit avec trois doigts, soit avec la main entière, et la règle du tire-bouchon (ou de la vis) . Vous pouvez utiliser n’importe laquelle d’entre elles, vous n’avez donc pas besoin de toutes les connaître, nous vous expliquerons quand même les trois règles afin que vous puissiez vous en tenir à celle que vous préférez. 😉

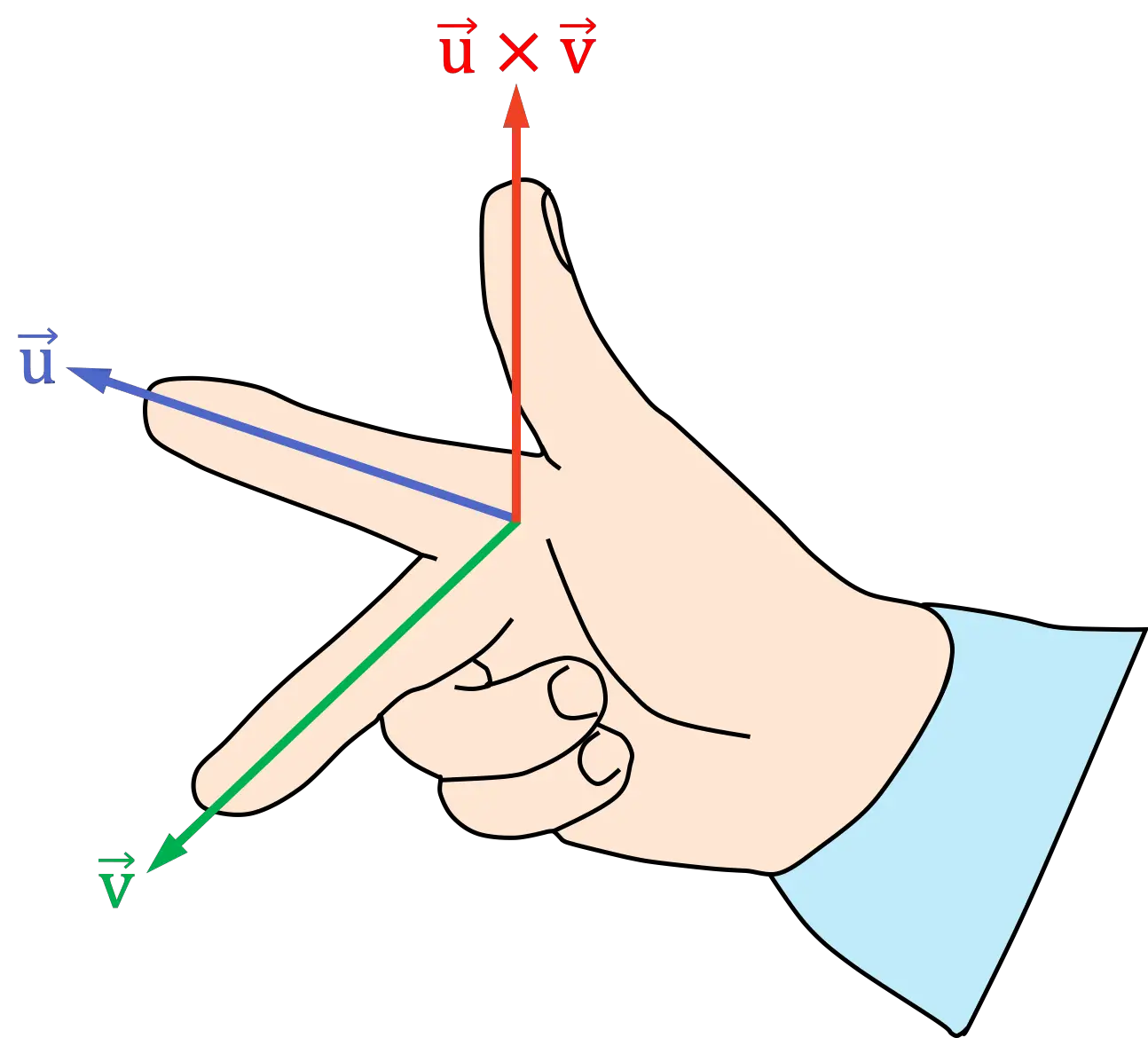
Règle de la main droite (3 doigts)

La version de la règle ou loi de la main droite à 3 doigts consiste à effectuer les étapes suivantes :

Placez l’index de votre main droite en direction du premier vecteur du produit vectoriel $(\vv{\text{u}}).$
Placez le majeur (ou majeur) de votre main droite en direction du deuxième vecteur du produit vectoriel $(\vv{\text{v}}).$
La position résultante du pouce indique la direction et le sens du produit vectoriel $(\vv{\text{u}}\times\vv{\text{v}}).$

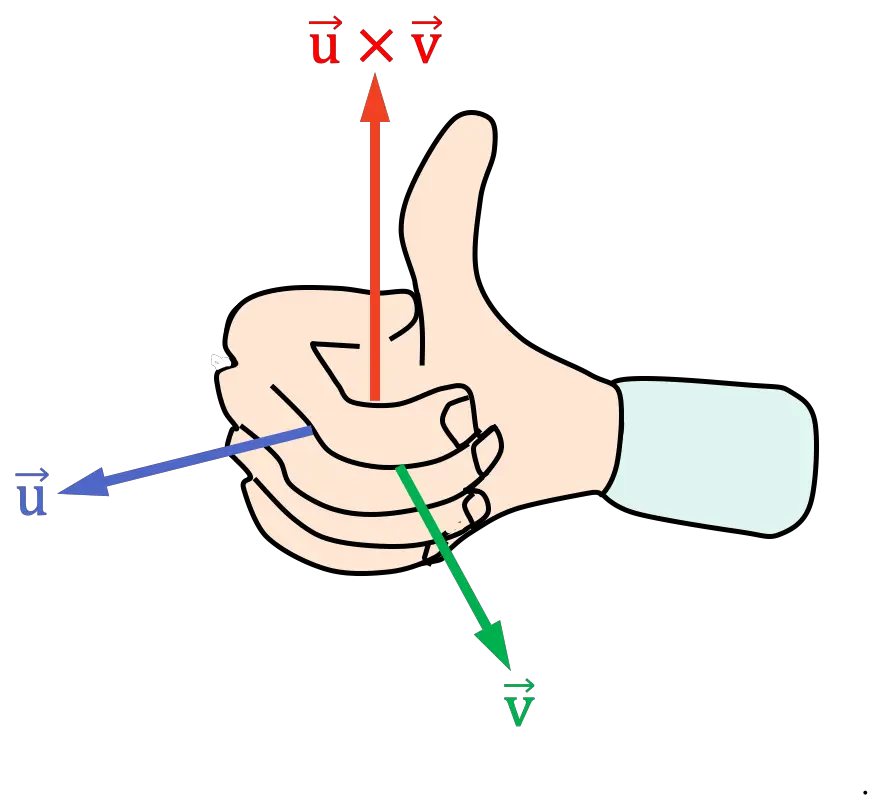
Règle de la main droite (paume de la main)

La version palmaire de la règle ou loi de la main droite est très similaire à la règle précédente. Pour l’appliquer, vous devez suivre les étapes suivantes :

Mettez votre main droite pointant avec vos doigts dans la même direction que le premier vecteur du produit vectoriel $(\vv{\text{u}}).$
Fermez votre main droite en déplaçant vos doigts vers le deuxième vecteur du produit vectoriel $(\vv{\text{v}}).$ Vous devez fermer votre main du côté où l’angle (ou la distance) entre les vecteurs est plus petit.
La position résultante du pouce détermine le sens et la direction du produit vectoriel $(\vv{\text{u}}\times\vv{\text{v}}).$

produit vectoriel de règle de la main droite

règle du tire-bouchon

La règle du tire-bouchon ou de la vis est similaire à la règle de la main droite utilisant toute la paume de la main. La procédure est la suivante :

En utilisant votre imagination, placez un tire-bouchon (ou une vis) avec la poignée pointant dans la même direction que le premier vecteur du produit vectoriel. $(\vv{\text{u}}).$
Tournez ensuite le tire-bouchon vers le deuxième vecteur du produit vectoriel 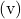$(\vv{\text{v}})$ comme si vous alliez le mettre dans un bouchon. Vous devez tourner le tire-bouchon du côté où la distance entre les vecteurs est la plus courte.
La direction dans laquelle pointe la spirale du tire-bouchon sera la direction et le sens du produit vectoriel $(\vv{\text{u}}\times\vv{\text{v}}).$

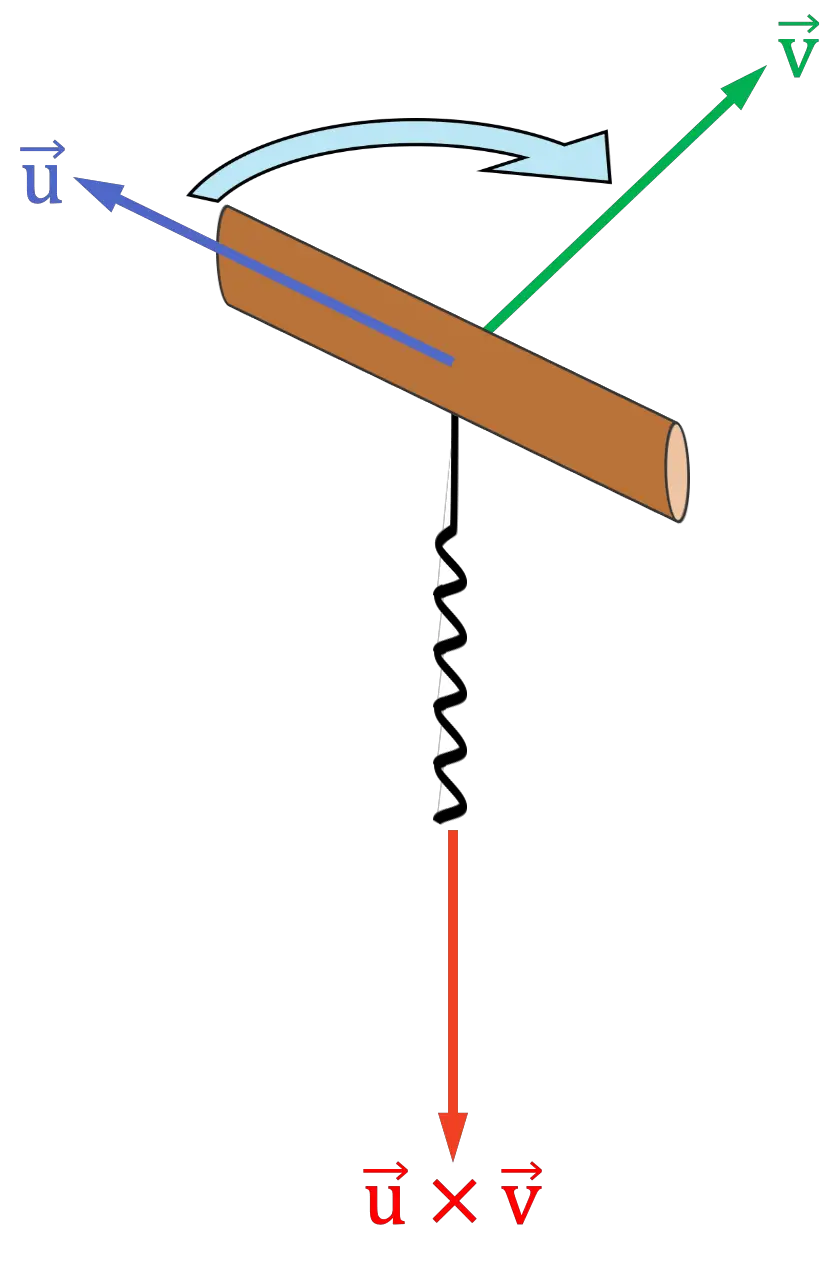
Propriétés du produit vectoriel de deux vecteurs

Le produit vectoriel de deux vecteurs a les caractéristiques suivantes :

Propriété anticommutative : l’ordre des vecteurs impliqués dans le produit vectoriel n’est pas indifférent, car le signe varie en fonction de lui.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

Propriété distributive concernant l’addition et la soustraction de vecteurs :

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

Propriété homogène : multiplier un vecteur du produit vectoriel par un scalaire (un nombre réel) équivaut à multiplier le résultat du produit vectoriel par ledit scalaire.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

Le vecteur issu du produit vectoriel est perpendiculaire aux deux vecteurs intervenus dans l’opération.

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

De plus, si les deux vecteurs sont orthogonaux, les équations suivantes sont satisfaites :

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

Le produit vectoriel de deux vecteurs parallèles est égal au vecteur nul (ou zéro).

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

Si l’on ne connaît pas l’angle formé par deux vecteurs, le module de leur produit vectoriel peut également être calculé à l’aide de l’expression suivante :

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

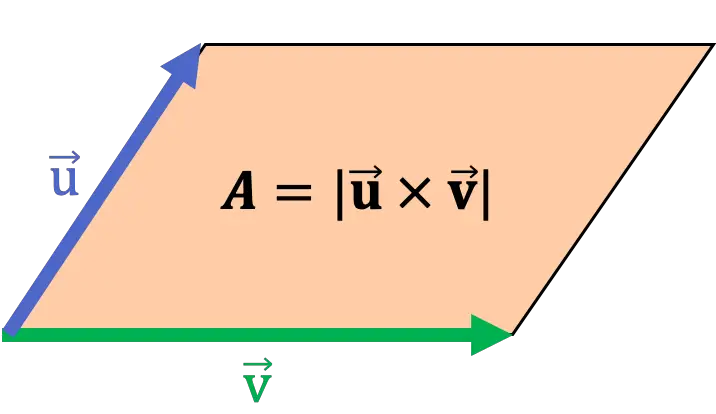
Calculer l’aire d’un parallélogramme ou d’un triangle à l’aide du produit vectoriel

Géométriquement, le module du produit vectoriel de deux vecteurs coïncide avec l’aire du parallélogramme qui a ces deux vecteurs comme côtés. Par conséquent, le produit vectoriel peut être utilisé pour calculer l’aire d’un parallélogramme.

produit vectoriel de deux vecteurs dans l'espace

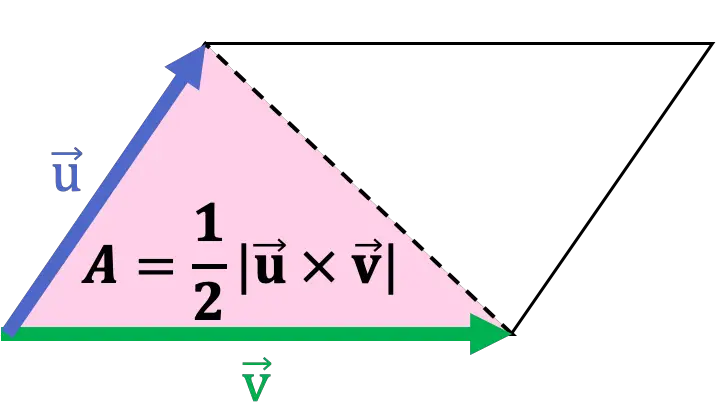
De plus, la diagonale d’un parallélogramme le divise en deux triangles, ou en d’autres termes, un triangle est la moitié d’un parallélogramme. Ainsi, l’ aire d’un triangle est la moitié du module du produit vectoriel en prenant deux de ses côtés comme vecteurs.

produit vectoriel de deux vecteurs dans r2

Rappelons que le module d’un vecteur dans un espace à 3 dimensions est la racine de la somme des carrés de ses coordonnées :

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Ce sont deux des applications du produit vectoriel de deux vecteurs dans le domaine des mathématiques. Cependant, il a encore d’autres utilisations, par exemple en physique, il est utilisé pour calculer le champ magnétique.

Exercices résolus sur les produits vectoriels de vecteurs

Exercice 1

Calculez le produit vectoriel entre les deux vecteurs suivants :

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

Voir la solution

Pour déterminer le produit vectoriel entre les vecteurs, il faut résoudre le déterminant suivant de dimension 3×3 :

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

Dans ce cas, nous résoudrons le déterminant par adjuvants ou cofacteurs (mais la règle de Sarrus pourrait aussi être utilisée) :

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

Le résultat du produit vectoriel des deux vecteurs est donc :

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

Exercice 2

Trouvez le produit vectoriel entre les deux vecteurs suivants :

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

Voir la solution

Pour trouver le produit vectoriel entre les deux vecteurs, il faut résoudre le déterminant 3×3 suivant :

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

Dans ce cas, nous résoudrons le déterminant par des adjoints ou des cofacteurs (bien que la règle de Sarrus puisse être utilisée de manière interchangeable) :

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

Le résultat du produit vectoriel entre les deux vecteurs est donc :

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

Exercice 3

Connaissant les modules de deux vecteurs et l’angle qu’ils forment :

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

Déterminez la grandeur du produit vectoriel des deux vecteurs.

Voir la solution

On peut facilement calculer le module du produit vectoriel entre les deux vecteurs en appliquant la formule :

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

Exercice 4

A partir des vecteurs suivants contenus dans le plan écran :

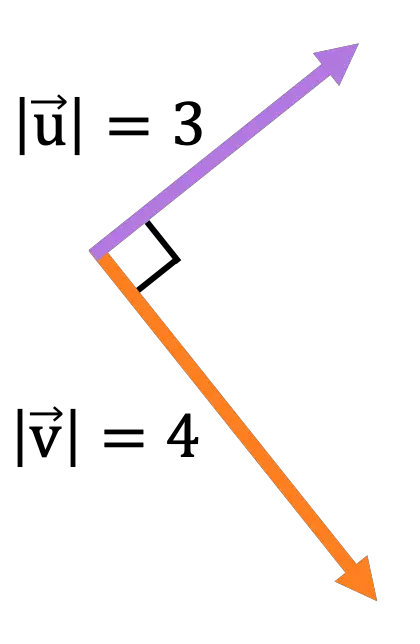
produit vectoriel de deux vecteurs en ligne

Calculez l’amplitude, la direction et le sens du vecteur résultant de l’opération vectorielle suivante :

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

Voir la solution

Les deux vecteurs sont perpendiculaires, donc la norme du produit vectoriel sera :

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

En revanche, le vecteur issu du produit vectoriel est perpendiculaire aux deux vecteurs qui participent à l’opération, sa direction sera donc perpendiculaire à l’écran.

Et enfin, en utilisant la règle de la droite (ou du tire-bouchon), on peut en déduire que la direction du vecteur résultant sera vers l’intérieur de l’écran.

Exercice 5

Calculez l’aire du parallélogramme qui a les vecteurs suivants comme deux de ses côtés :

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

Voir la solution

L’aire d’un parallélogramme coïncide avec le module du produit vectoriel des vecteurs qui le forment. On calcule donc le produit vectoriel des vecteurs :

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

Et puis votre module :

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

Exercice 6

Trouver l’aire du triangle dont les sommets sont les points suivants :

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

Voir la solution

Tout d’abord, il faut calculer les vecteurs qui forment les côtés du triangle :

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

L’aire d’un triangle est la moitié de la grandeur du produit vectoriel des vecteurs qui le forment. On calcule donc le produit vectoriel des vecteurs :

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

Après votre module :

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

Et enfin, l’aire du triangle sera la moitié du module :

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

Produit vectoriel de deux vecteurs (ou produit croisé)

Quel est le produit vectoriel de deux vecteurs ?

Formule pour calculer le produit vectoriel de deux vecteurs

Déterminer la direction et le sens du produit vectoriel

Règle de la main droite (3 doigts)

Règle de la main droite (paume de la main)

règle du tire-bouchon

Propriétés du produit vectoriel de deux vecteurs

Calculer l’aire d’un parallélogramme ou d’un triangle à l’aide du produit vectoriel

Exercices résolus sur les produits vectoriels de vecteurs

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Leave a Comment Cancel Reply