Nous expliquons ici comment les problèmes d’optimisation des fonctions sont résolus par étapes. De plus, vous pourrez vous entraîner avec des exercices résolus sur des problèmes d’optimisation.
Quels sont les problèmes d’optimisation ?
Les problèmes d’optimisation sont des problèmes dans lesquels il faut trouver le maximum ou le minimum d’une fonction. Par exemple, un problème d’optimisation consisterait à calculer le maximum d’une fonction qui définit les bénéfices d’une entreprise.
Comment résoudre les problèmes d’optimisation
Étapes pour résoudre les problèmes d’optimisation des fonctions :
- Pose la fonction qui doit être optimisée.
- Dérivez la fonction à optimiser.
- Trouver les points critiques de la fonction à optimiser. Pour ce faire, vous devez définir la dérivée de la fonction égale à zéro et résoudre l’équation résultante.
- Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Exemple de problème d’optimisation
Compte tenu de la théorie des problèmes d’optimisation, nous allons résoudre un problème de ce type étape par étape afin que vous puissiez voir comment ils sont réalisés.
- Parmi tous les triangles rectangles dont les pattes totalisent 10 cm, calculez les dimensions de celui qui a la surface maximale.
Pour résoudre le problème, nous appellerons une branche du triangle x , et l’autre branche y :

Étape 1 : Posez la fonction à optimiser.
Nous voulons que l’aire du triangle soit maximale, et la formule pour l’aire d’un triangle est :
![]()
Dans notre cas, la base du triangle est x et sa hauteur est y . Pourtant:
![]()
On a déjà la fonction à optimiser, mais elle dépend de deux variables alors qu’elle ne peut dépendre que d’une seule. Cependant, la déclaration nous dit que les deux jambes doivent totaliser 10 cm. Pourtant:
![]()
Nous résolvons y à partir de cette équation :
![]()
Et on substitue l’expression dans la fonction :
![]()
![]()
Nous avons maintenant la fonction d’optimisation planifiée et elle ne dépend que d’une seule variable, nous pouvons donc passer à l’étape suivante.
Étape 2 : Calculez la dérivée de la fonction à optimiser.
C’est une fonction rationnelle, nous appliquons donc la formule de la dérivée d’une division pour la dériver :
![]()
![]()
Étape 3 : Trouvez les points critiques.
Pour trouver les points critiques de la fonction, nous devons mettre la dérivée égale à zéro et résoudre l’équation résultante :
![]()
![]()
Le 4 divise tout le côté gauche, on peut donc le multiplier en multipliant tout le côté droit :
![]()
![]()
![]()
![]()
![]()
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Pour étudier la monotonie de la fonction, on représente le point critique trouvé sur la droite :
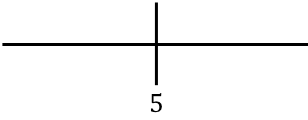
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle pour savoir si la fonction augmente ou diminue. Pour ce faire, nous prenons un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
![]()
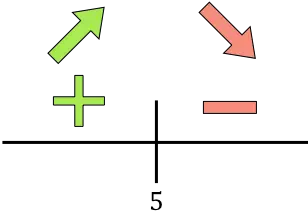
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles d’augmentation et de diminution de la fonction sont :
Croissance:
![]()
Diminuer:
![]()
À x=5 la fonction passe de croissante à décroissante, donc x=5 est un maximum relatif de la fonction à optimiser .
Par conséquent, x=5 est la valeur de la branche du triangle qui fait l’aire maximale. Il suffit de calculer la valeur de l’autre jambe :
![]()
En conclusion, les valeurs qui maximisent l’aire maximale du triangle sont :
![]()
![]()
Problèmes d’optimisation résolus
Problème 1
Le médicament est administré à une personne malade et
![]() quelques heures plus tard, la concentration sanguine du principe actif est donnée par la fonction
quelques heures plus tard, la concentration sanguine du principe actif est donnée par la fonction![]() milligrammes par millilitre. Détermine la valeur maximale de
milligrammes par millilitre. Détermine la valeur maximale de![]() et indique quand ladite valeur est atteinte.
et indique quand ladite valeur est atteinte.
Étape 1 : Posez la fonction à optimiser.
Dans ce problème, ils nous donnent déjà la fonction proposée, qui est
![]()
Étape 2 : Calculez la dérivée de la fonction à optimiser.
La fonction est composée du produit de 2 fonctions. Par conséquent, pour calculer la dérivée de la fonction, nous devons appliquer la règle de la dérivée d’un produit :
![]()
![]()
Étape 3 : Trouvez les points critiques.
Pour trouver les points critiques de la fonction, on résout
![]()
![]()
![]()
On prend le facteur commun pour résoudre l’équation :
![]()
Pour que la multiplication soit égale à 0, il faut qu’un des deux éléments de la multiplication soit nul. Par conséquent, nous fixons chaque facteur égal à 0 :
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
Un nombre élevé à un autre nombre ne peut jamais donner 0, donc,
![]() Il n’y a pas de solution.
Il n’y a pas de solution.
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Pour étudier la monotonie de la fonction, on représente le point critique trouvé sur la droite :
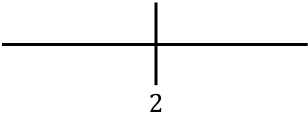
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
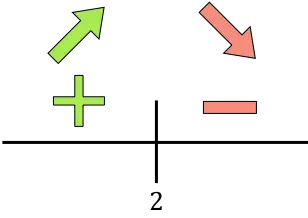
Si la dérivée est positive cela signifie que la fonction augmente, par contre si la dérivée est négative cela signifie que la fonction diminue. Ainsi les intervalles de croissance et de diminution de la fonction à optimiser sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à t=2, donc t=2 est un maximum de la fonction. La concentration maximale sera donc atteinte en t=2 heures.
Enfin, nous substituons la valeur à laquelle le maximum se produit dans la fonction d’origine, pour trouver la valeur de la concentration maximale :
![]()
Problème 2
Un magasin espère vendre 40 scooters électriques au prix de 1 000 € par scooter. Mais selon une étude de marché, pour chaque réduction de 50 € sur le prix du scooter, il y aura une augmentation des ventes des 10 scooters les plus vendus.
Écrivez d’abord la fonction de revenus du magasin en fonction du nombre de fois où le prix initial de 1 000 € du scooter est réduit de 50 €. Ensuite, déterminez le prix du scooter pour obtenir un maximum de profits et les revenus gagnés à ce prix.
Étape 1 : Posez la fonction à optimiser.
L’énoncé du problème nous donne un indice, puisqu’il nous indique que la fonction doit dépendre du nombre de fois où le prix initial est réduit de 50 €. On appellera donc x le nombre de fois où le prix est réduit de 50 € :
![]() €
€
La fonction de revenu sera le nombre de scooters vendus multiplié par le prix de chaque scooter :
![]()
Le nombre de scooters vendus sera de 40 plus 10 scooters pour chaque réduction de prix de 50 €. Pourtant:
![]()
Le prix de chaque scooter sera de 1000 € au début, et diminuera de 50 € à chaque baisse de prix. Pourtant:
![]()
La fonction pour optimiser le problème est donc :
![]()
![]()
![]()
![]()
Étape 2 : Calculez la dérivée de la fonction à optimiser.
Étant une fonction polynomiale, la dérivée est plus facile à calculer :
![]()
Étape 3 : Trouver les points critiques de la fonction.
Pour trouver les points critiques de la fonction, on résout
![]()
![]()
![]()
![]()
![]()
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Pour étudier la monotonie de la fonction, nous représentons le point critique calculé sur la droite numérique :
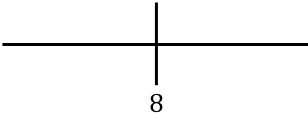
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
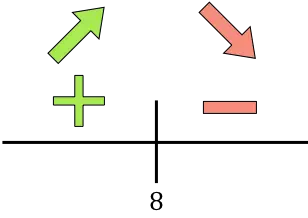
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à x=8, donc x=8 est un maximum de la fonction. Par conséquent, le revenu maximum sera obtenu en effectuant 8 fois la réduction de 50 €.
Nous substituons maintenant la valeur à laquelle le revenu maximum apparaît dans la fonction d’origine, pour trouver la valeur du revenu maximum :
![]()
![]() €
€
Et le prix de chaque scooter après avoir effectué 8 fois la remise de 50 € sera :
![]()
![]() €
€
Problème 3
La fonction de coût (en milliers d’euros) d’une entreprise peut être déterminée à l’aide de l’expression suivante :
![]()
Où
![]() représente les milliers d’unités produites d’un article donné.
représente les milliers d’unités produites d’un article donné.
Déterminez la quantité qui doit être produite pour que le coût soit minime, quel est ce coût et quel serait le coût si aucun de ces articles n’était produit.
Étape 1 : Posez la fonction à optimiser.
L’énoncé du problème nous fournit déjà la fonction à optimiser, qui est
![]()
Étape 2 : Calculez la dérivée de la fonction à optimiser.
![]()
Étape 3 : Trouvez les points critiques.
Pour trouver les points critiques de la fonction, on résout
![]()
![]()
![]()
![]()
![]()
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Nous représentons le point critique trouvé sur la droite :
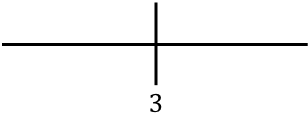
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
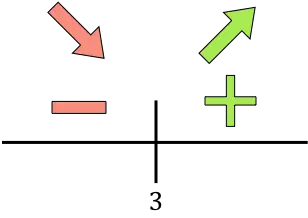
Si la dérivée est supérieure à zéro, la fonction croît sur cet intervalle. En revanche, si la dérivée est inférieure à zéro, la fonction diminue dans cet intervalle. Ainsi, les intervalles de croissance et de décroissance de la fonction sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de décroissante à croissante à x=3, donc x=3 est un minimum de la fonction. Par conséquent, le coût minimum sera atteint en produisant 3 000 unités.
Nous substituons maintenant la valeur à laquelle le coût minimum est atteint dans la fonction d’origine pour trouver la valeur du coût minimum :
![]() des milliers d’euros.
des milliers d’euros.
En revanche, ils nous demandent quel serait le coût si rien n’était produit, c’est-à-dire lorsque
![]() Il faut donc calculer
Il faut donc calculer![]()
![]() des milliers d’euros.
des milliers d’euros.
Problème 4
Nous souhaitons construire une charpente rectangulaire en bois qui délimite une superficie de 2 m 2 . On sait que le prix du bois est de 7,5 €/m pour les côtés horizontaux et de 12,5 €/m pour les côtés verticaux. Déterminez les dimensions que doit avoir le rectangle pour que le coût total du cadre soit le minimum possible et que ledit coût soit minimum.
Étape 1 : Posez la fonction à optimiser.
Pour résoudre le problème, nous appellerons le côté horizontal x , et le côté vertical y :

L’achat d’un côté horizontal coûte 7,5 € et l’achat d’un côté vertical coûte 12,5 €. De plus, pour chaque cadre, nous avons besoin de deux côtés horizontaux et de deux côtés verticaux. Par conséquent, le coût du cadre peut être déterminé avec la fonction suivante :
![]()
Nous avons déjà la fonction à optimiser. Mais cela dépend de deux variables alors qu’il ne peut dépendre que d’une seule. Cependant, l’énoncé nous indique que la superficie de la charpente doit être de 2 m 2 . Pourtant:
![]()
On efface la variable y :
![]()
Et on substitue l’expression trouvée dans la fonction à optimiser :
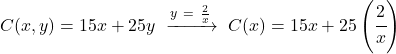
![]()
Étape 2 : Calculez la dérivée de la fonction à optimiser.
![]()
Étape 3 : Trouvez les points critiques.
Pour trouver les points critiques de la fonction, on résout
![]()
![]()
![]()
![]()
![]()
![]()
On multiplie transversalement pour résoudre l’équation avec des fractions :
![]()
![]()
![]()
![]()
![]()
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Nous représentons le point critique trouvé pour analyser la monotonie de la fonction sur la ligne :
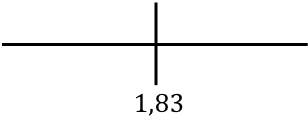
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
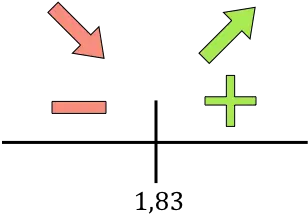
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de décroissante à croissante à x=1,83, donc x=1,83 est un minimum de la fonction.
Par conséquent, x=1,83 est la valeur du côté horizontal qui représente le coût minimum. Calculons maintenant la valeur du côté vertical :
![]()
Ainsi, les valeurs qui composent le coût du framework minimum sont :
côté horizontal
![]()
côté vertical
![]()
Et le coût minimum atteint avec ces valeurs est :
![]() €
€
Problème 5
La porte d’une cathédrale est formée par un arc en demi-circonférence soutenu par deux colonnes, comme le montre la figure suivante :
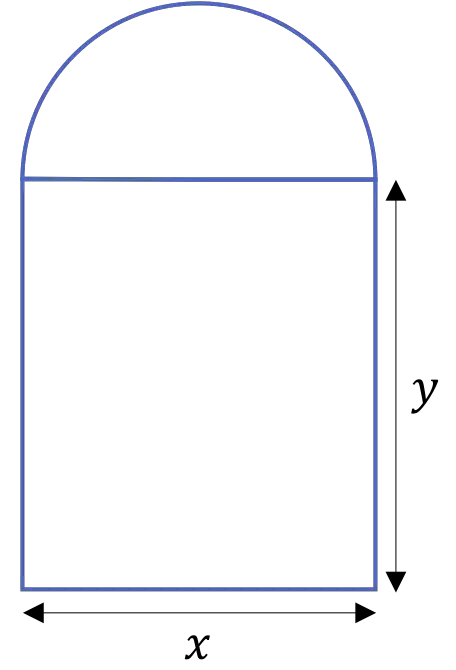
Si le périmètre de la porte est de 20 m, déterminez les mesures
![]() et
et![]() qui maximisent la surface de toute la porte.
qui maximisent la surface de toute la porte.
Étape 1 : Posez la fonction à optimiser.
L’aire d’un cercle est calculée avec la formule
![]() Ainsi, l’aire de la porte entière sera l’aire du rectangle plus la moitié de l’aire de la circonférence :
Ainsi, l’aire de la porte entière sera l’aire du rectangle plus la moitié de l’aire de la circonférence :
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
Nous avons déjà la fonction à optimiser. Mais cela dépend de deux variables alors qu’il ne peut dépendre que d’une seule.
Cependant, le communiqué nous indique que le périmètre de la porte entière est de 20 m. Le périmètre d’un cercle se calcule avec la formule
![]() Par conséquent, le périmètre de la porte entière sera :
Par conséquent, le périmètre de la porte entière sera :
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
Le périmètre doit être de 20 m. Nous fixons donc l’expression précédente égale à 20 pour trouver la relation entre
![]() et
et ![]()
![]()
On multiplie tous les termes par 2 pour éliminer les fractions :
![]()
![]()
Nous dégageons
![]()
![]()
![]()
Et on substitue l’expression trouvée dans la fonction à optimiser :
![]()
![]()
![]()
Étape 2 : Calculez la dérivée de la fonction à optimiser.
![]()
![]()
Étape 3 : Trouvez les points critiques.
Pour trouver les points critiques de la fonction, on résout
![]()
![]()
![]()
Il s’agit d’une équation avec des fractions, on multiplie donc chaque terme par le lcm des dénominateurs pour éliminer les fractions :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Pour étudier la monotonie de la fonction, on représente le point critique trouvé sur la droite :
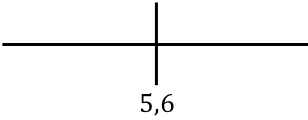
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
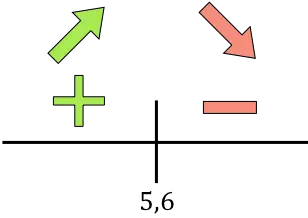
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à x=5,6, donc x=5,6 est un maximum de la fonction.
Pourtant,
![]() est la valeur qui fait la surface maximale. Maintenant on calcule la valeur de
est la valeur qui fait la surface maximale. Maintenant on calcule la valeur de ![]()
![]()
Ainsi, les valeurs qui font la surface maximale sont :
![]()
![]()
Problème 6
Nous voulons construire un réservoir en forme de cylindre d’une superficie de 54 cm 2 . Déterminez le rayon de la base et la hauteur du cylindre pour que le volume soit maximum.
Étape 1 : Posez la fonction à optimiser.
Le volume d’un cylindre se calcule avec la formule suivante :
![]()
L’aire de la base est un cercle, donc sa formule est
![]() . La formule du volume du cylindre est donc :
. La formule du volume du cylindre est donc :
![]()
Nous avons déjà la fonction à optimiser. Mais cela dépend de deux variables (
![]() et
et![]() ) alors que cela ne peut dépendre que d’un seul. Cependant, l’énoncé nous dit que l’aire du cylindre doit être de 54 cm 2 , nous profiterons donc de cette condition pour trouver la relation entre
) alors que cela ne peut dépendre que d’un seul. Cependant, l’énoncé nous dit que l’aire du cylindre doit être de 54 cm 2 , nous profiterons donc de cette condition pour trouver la relation entre![]() et
et![]()
Pour calculer l’aire d’un cylindre il faut additionner son aire latérale avec les aires des deux bases :
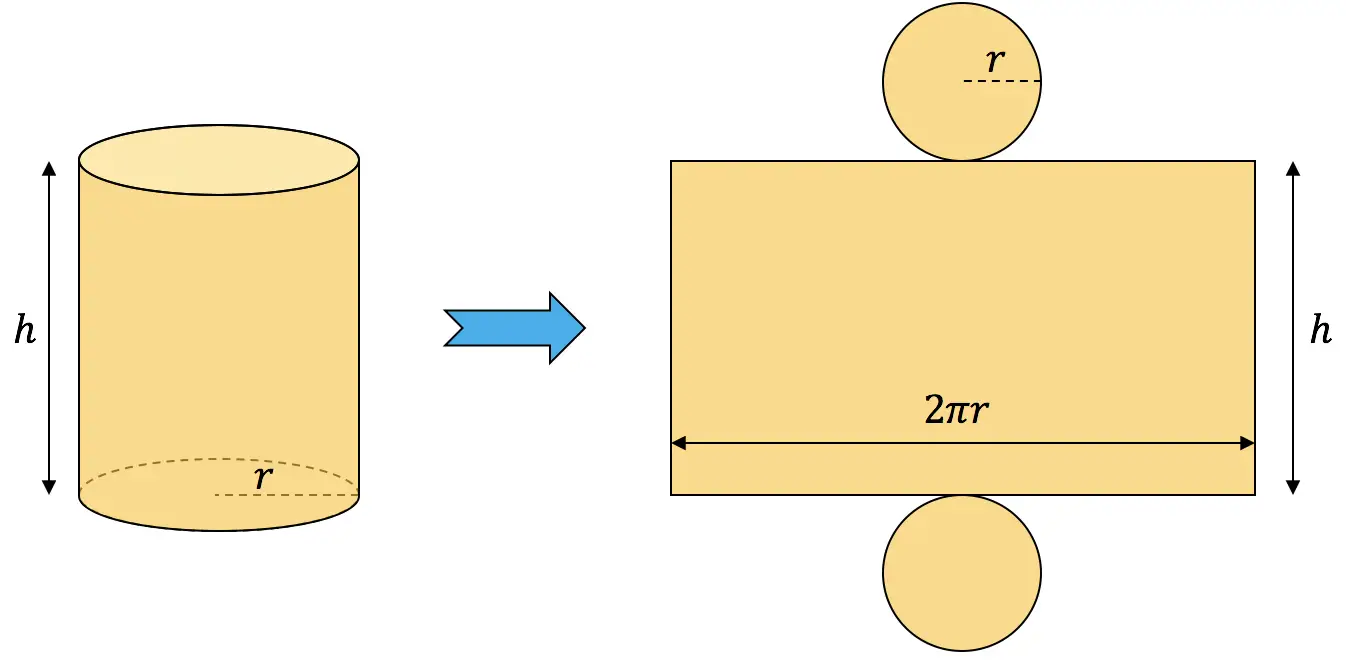
![]()
L’aire du cylindre doit être de 54 cm 2 , nous fixons donc l’expression précédente égale à 54 pour obtenir la relation entre
![]() et
et ![]()
![]()
Nous dégageons
![]()
![]()
![]()
Et on substitue l’expression trouvée dans la fonction à optimiser :
![]()
![]()
![]()
Étape 2 : Calculez la dérivée de la fonction à optimiser.
![]()
Étape 3 : Trouvez les points critiques.
Pour trouver les points critiques de la fonction, on résout
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Étape 4 : Étudiez la monotonie de la fonction et déterminez le maximum ou le minimum de la fonction.
Pour étudier la monotonie de la fonction, nous représentons le point critique trouvé sur la droite numérique :
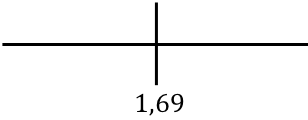
Et maintenant nous évaluons le signe de la dérivée dans chaque intervalle, pour savoir si la fonction augmente ou diminue. Nous prenons donc un point dans chaque intervalle (jamais le point critique) et regardons quel signe la dérivée a à ce point :
![]()
![]()
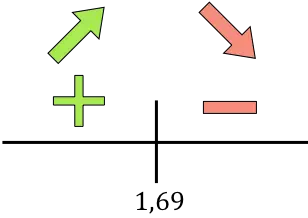
Si la dérivée est positive, cela signifie que la fonction augmente, et si la dérivée est négative, cela signifie que la fonction diminue. Par conséquent, les intervalles de croissance et de diminution sont :
Croissance:
![]()
Diminuer:
![]()
La fonction passe de croissante à décroissante à r=1,69, donc r=1,69 cm est un maximum de la fonction.
Par conséquent, r=1,69 est la valeur du rayon qui fait le volume maximum. Maintenant, nous calculons la hauteur :
![]()
Ainsi les valeurs qui font le volume maximum sont :
Radio
![]()
Hauteur
![]()