Positions relatives d'une droite et d'un plan

Sur cette page vous trouverez les positions relatives d’une droite et d’un plan. Nous vous expliquons comment se calcule la position relative entre une droite et un plan (2 méthodes) et, en plus, vous pourrez voir des exemples et des exercices résolus pas à pas.

Quelles sont les positions relatives entre une droite et un plan ?

Avant de regarder toutes les positions relatives possibles entre une droite et un plan, il faut évidemment savoir ce que sont des droites et ce qu’est un plan . Donc si vous n’avez toujours pas ces deux notions très claires, nous vous recommandons de jeter d’abord un œil aux pages liées où c’est expliqué en détail.

Ainsi, en géométrie analytique, il n’y a que trois positions relatives dans l’espace entre une droite et un plan :

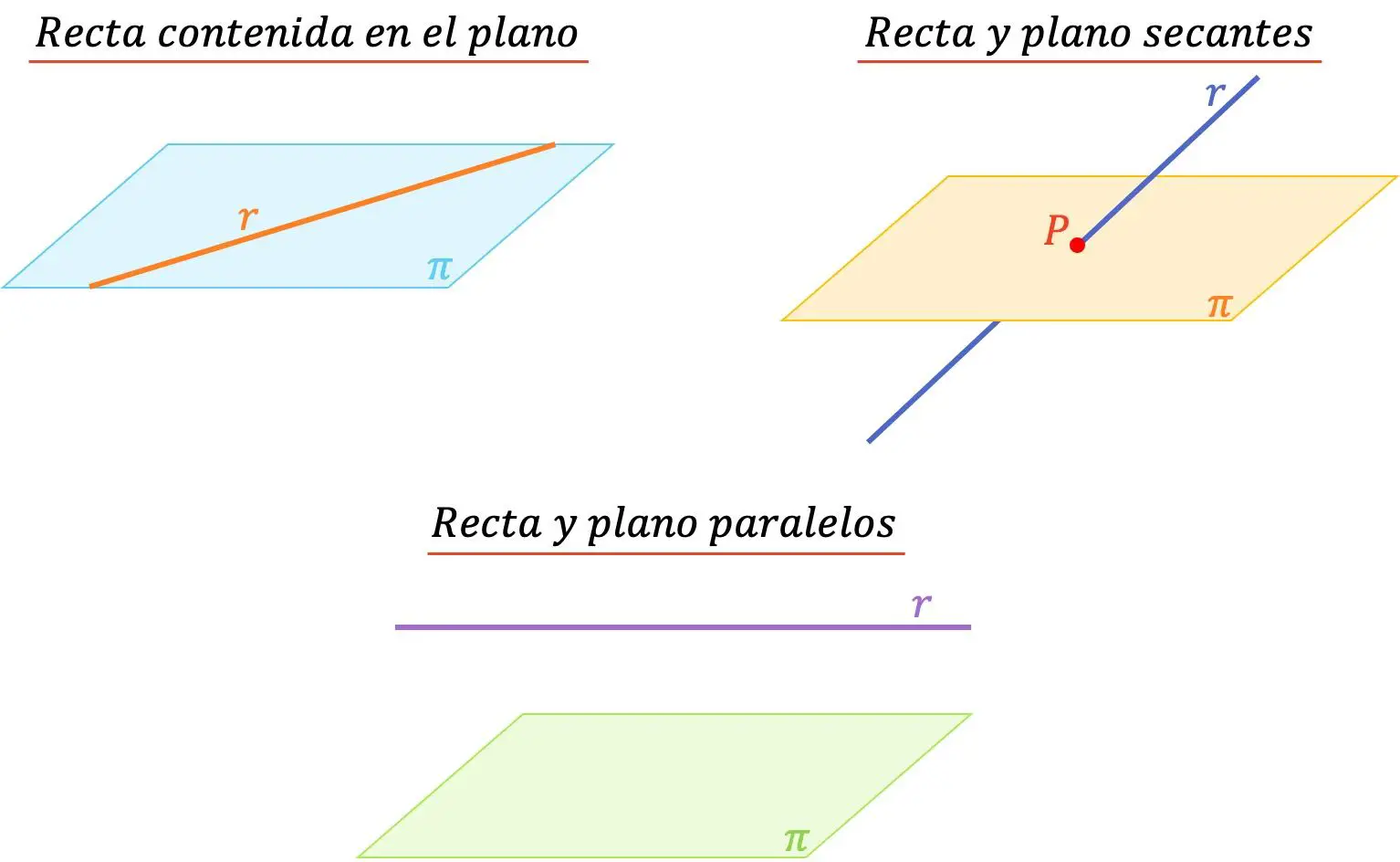
Ligne contenue dans le plan : lorsque la ligne est contenue dans le plan cela signifie qu’elles ont une infinité de points en commun.
Droite et plan parallèles : Une droite et un plan sont parallèles lorsqu’ils n’ont aucun point en commun.
Ligne et plan sécants : Une ligne et un plan se coupent lorsque la ligne coupe le plan en un point. Ils n’ont donc qu’un point commun.

Par contre, lorsque la ligne est contenue dans le plan ou lorsqu’elles sont parallèles entre elles, l’angle qu’elles formeront sera de 0º. Par contre, lorsque la ligne et le plan se coupent, l’angle entre les deux éléments géométriques peut aller de 0º (non inclus) à 90º (inclus).

Comment calculer la position relative d’une droite et d’un plan ?

Il existe principalement deux méthodes pour trouver la position relative entre une droite et un plan dans l’espace : par plages ou par vecteurs .

Lorsque la droite est exprimée sous la forme d’une équation implicite (ou générale), il est plus facile d’utiliser la méthode des rangs. En revanche, si la droite est donnée avec un autre type d’équation, par exemple lorsqu’elle est sous forme d’équation vectorielle, paramétrique ou continue, il est plus rapide d’utiliser la méthode vectorielle.

Si vous ne vous souvenez pas à quoi ressemblent les équations de la ligne, nous vous laissons une page où vous pouvez consulter toutes les équations de la ligne . Vous trouverez ici toutes les équations de la droite, une formule pour trouver rapidement l’équation d’une droite passant par deux points, des exemples et des exercices résolus pas à pas.

Par conséquent, il est plus pratique d’utiliser une méthode ou une autre en fonction du problème, pour cette raison nous vous recommandons de savoir comment faire les deux procédures. Vous trouverez ci-dessous l’explication des deux méthodes avec des exemples.

Lorsque la ligne est sous la forme d’une équation implicite (ou générale)

Une façon de déterminer la position relative entre une droite et un plan consiste à calculer le rang de deux matrices.

Si la droite est définie par ses équations implicites (ou générales) :

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

Et le plan s’exprime aussi sous la forme d’une équation générale :

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Nous appellerons A la matrice composée des coefficients A, B et C des équations du plan et de la droite :

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

Et la matrice A’ sera la matrice développée avec tous les coefficients des deux équations :

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Ensuite, la position relative entre la droite et le plan est déterminée par la valeur de l’étendue des deux matrices précédentes selon le tableau suivant :

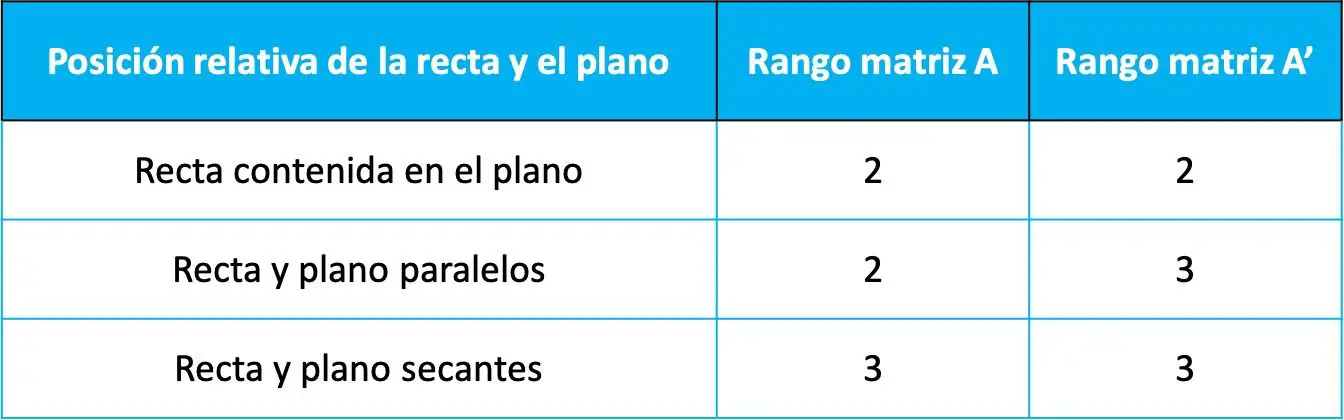
étudier la position relative entre une droite et un plan dans l'espace par plages

Que les positions relatives dépendent des rangs de ces deux matrices peut être montré à partir du toerem de Rouché-Frobenius (un théorème utilisé pour résoudre des systèmes d’équations linéaires). Cependant, sur cette page nous ne ferons pas la démonstration car il n’est pas nécessaire de la connaître et elle n’apporte pas grand chose non plus.

Exemple de comment trouver la position relative d’une ligne et d’un plan par plages

Pour que vous puissiez voir exactement comment cela se fait, nous allons résoudre un exercice à titre d’exemple :

Etudiez la position relative entre la droite suivante et le plan suivant :

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

La ligne est définie par deux plans sécants, c’est-à-dire qu’elle est exprimée sous la forme d’une équation implicite. Par conséquent, nous utiliserons la méthode des rangs pour étudier la position relative entre la droite et le plan.

La première chose à faire est de construire la matrice A et la matrice étendue A’ avec les coefficients des équations :

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

Et maintenant, nous devons calculer le rang de chaque matrice. On trouve d’abord l’étendue de la matrice A par déterminants :

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

Le déterminant de la matrice A est nul mais il contient une sous-matrice 2×2 dont le déterminant est différent de zéro, c’est donc une matrice de rang 2.

D’autre part, il faut aussi calculer le rang de la matrice A’. Et la plage de la matrice étendue A’ sera toujours au moins la même que celle de la matrice A, il suffit donc de vérifier si elle est de rang 3 ou 2 :

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

Par contre, la matrice étendue A’ possède bien un sous-déterminant 3×3 différent de 0, elle est donc de rang 3.

Donc, puisque la matrice A est de rang 2 et la matrice A’ est de rang 3, la droite et le plan sont parallèles .

Lorsque la ligne est sous la forme d’un autre type d’équation

Lorsque la droite est exprimée par une équation autre que celle implicite, que ce soit l’équation vectorielle, paramétrique ou continue, il est préférable d’utiliser la méthode que nous expliquons ci-dessous.

Ainsi, si la ligne est donnée sous la forme d’une équation vectorielle, d’équations paramétriques ou d’une équation continue, cela signifie que nous connaissons un point qui appartient à la ligne et, également, son vecteur directeur.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

D’autre part, nous savons aussi quel est le vecteur normal (ou perpendiculaire) au plan :

$\vv{n} \perp \pi$

Ensuite, à partir des 2 vecteurs et du point de la droite, la position relative entre la droite et le plan peut être calculée comme suit :

Si le produit scalaire entre le vecteur directeur de la droite et le vecteur normal au plan est différent de zéro, cela signifie que la droite est sécante au plan.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
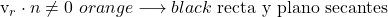
Mais si le produit scalaire entre le vecteur directeur de la droite et le vecteur normal au plan est égal à zéro, il y a deux possibilités : la droite est contenue dans le plan ou elles sont parallèles. Et pour savoir de quel cas il s’agit, il faut substituer les coordonnées d’un point sur la droite dans l’équation du plan.
- Si le point satisfait l’équation du plan, la droite est contenue dans le plan.
- Par contre, si le point ne satisfait pas l’équation du plan, la droite et le plan sont parallèles.

Exemple de détermination de la position relative d’une droite et d’un plan par des vecteurs

Une fois que nous avons vu la théorie de cette méthode, voyons maintenant un exercice résolu étape par étape :

Trouvez la position relative entre la ligne suivante et le plan suivant :

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Tout d’abord, la ligne est définie sous forme d’équations paramétriques, donc son vecteur directeur et un point par lequel elle passe sont :

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

Et, d’autre part, le vecteur normal au plan est :

$\vv{n} =(2,1,-2)$

Une fois que l’on connaît le vecteur directeur de la droite et le vecteur normal au plan, il faut calculer le produit scalaire entre les deux :

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Le résultat du produit scalaire est nul, de sorte que la ligne ne peut être contenue que dans le plan ou lui être parallèle. Donc, pour savoir de quel cas il s’agit, nous substituons les coordonnées cartésiennes du point sur la droite dans l’équation du plan :

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

En substituant le point de la droite dans l’équation du plan on obtient une égalité, donc le point respecte l’équation du plan et, par conséquent, la droite est contenue dans le plan .

Positions relatives d’une droite et d’un plan