Position relative de deux lignes dans l'espace

Vous trouverez ici toutes les positions relatives de deux droites dans l’espace (en R3). De plus, il explique comment trouver la position relative entre deux lignes en utilisant les 2 méthodes possibles : par plages ou à partir d’un point et d’un vecteur de chaque ligne. Vous pourrez même voir des exemples et des exercices résolus étape par étape.

Quelles sont les positions relatives de deux droites dans l’espace ?

En géométrie analytique, lorsque l’on travaille dans un espace à trois dimensions (en R3) il existe 4 positions relatives possibles entre deux droites : deux droites peuvent être des droites confondues , des droites parallèles , des droites sécantes ou des droites sécantes .

Lignes parallèles

position relative de deux droites parallèles

Deux droites sont parallèles si elles ont la même direction mais n’ont pas de point commun. De plus, les lignes parallèles sont toujours à la même distance les unes des autres.

lignes coïncidentes

position relative de deux droites coïncidentes

Deux droites sont confondues si elles ont la même direction et, de plus, si tous leurs points sont communs.

lignes sécantes

position relative de deux lignes qui se croisent

Deux lignes qui se croisent ont des directions différentes mais se touchent en un point.

Lignes d’intersection

Deux lignes qui se croisent ont des directions différentes et ne se croisent en aucun point. Par conséquent, deux lignes croisées ne sont pas dans le même plan. Par exemple, dans la représentation graphique au-dessus de la ligne

$s$ est toujours en avance sur la ligne $r$ , ainsi ils ne se toucheront jamais.

Il y a 2 façons de savoir quelle est la position relative entre deux droites, puisqu’elles dépendent de la façon dont les équations des deux droites sont exprimées :

Si les lignes sont sous forme d’équation vectorielle, paramétrique ou continue, il est préférable de calculer la position relative à partir d’un point et d’un vecteur de chaque ligne (l’explication de cette méthode est donnée ci-dessous).
En revanche, si les droites sont définies sous forme d’équations implicites (ou générales), il est plus facile de connaître la position relative entre les deux droites en calculant le rang de deux matrices (voir l’explication ci-dessous).

Détermination de la position relative de deux lignes à partir d’un point et d’un vecteur

Vous pouvez trouver quelle position relative il y a entre deux lignes avec un point et un vecteur de chaque ligne. Cette méthode est appropriée à utiliser lorsque les lignes sont définies sous la forme d’une équation vectorielle, d’équations paramétriques ou d’une équation continue.

Ainsi, soit le vecteur directeur et tout point de chacune des deux droites :

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Ainsi, pour trouver la position relative de deux lignes, nous devons suivre la procédure suivante :

‣ La première chose que nous devons faire est de voir si les vecteurs des deux lignes sont proportionnels ou non et, selon le cas, nous procédons comme suit :

Si les deux vecteurs sont proportionnels, les droites peuvent être parallèles ou confondues. Il faut donc vérifier si le point d’une droite satisfait l’équation de l’autre droite :
- Si le point d’une droite satisfait l’équation de l’autre droite, cela signifie que les deux droites coïncident.
- Sinon, cela implique que les deux droites sont parallèles.

Si les deux vecteurs ne sont pas proportionnels, les lignes peuvent être sécantes ou sécantes. Dans ce cas nous devons résoudre le déterminant 3×3 suivant :

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Si le déterminant précédent est égal à zéro, les deux droites se coupent en un point (elles se coupent).
- Si le déterminant précédent est différent de zéro, les deux droites se coupent.

Le graphique suivant résume l’ensemble de la procédure :

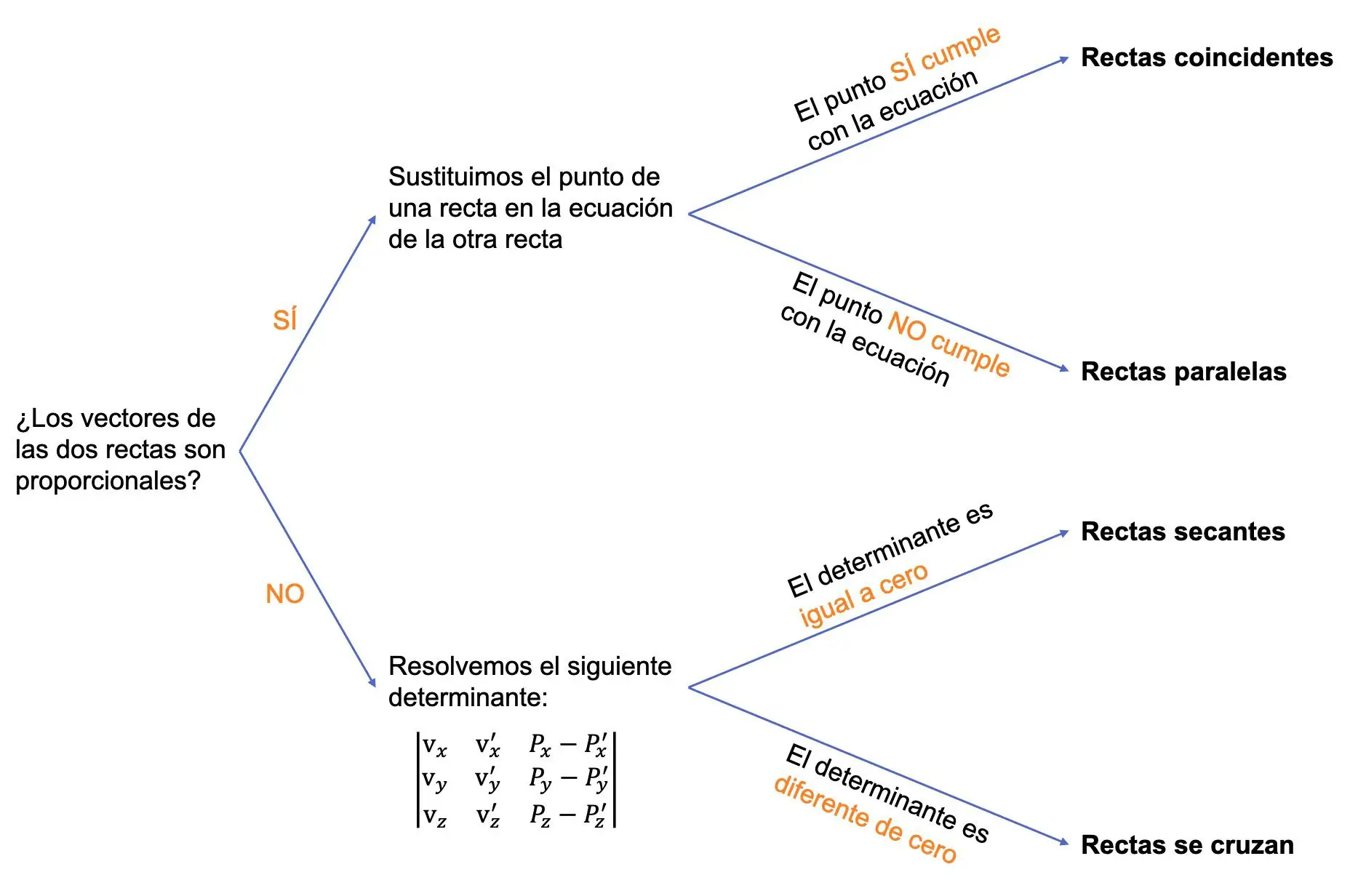
Exemple de détermination de la position relative entre deux lignes

La procédure précédente peut sembler un peu compliquée, mais pour que vous puissiez voir que c’est le contraire, nous allons résoudre un problème à titre d’exemple :

Déterminez la position relative entre les deux lignes suivantes :

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

Les deux lignes sont exprimées sous la forme d’une équation vectorielle, avec laquelle le vecteur directeur de chaque ligne est :

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

Et un point par lequel passe chaque ligne est :

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Une fois que l’on connaît un point et le vecteur directeur de chaque droite, on applique la méthode vue plus haut. Avant toute chose, il faut vérifier si les coordonnées des vecteurs sont proportionnelles :

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

Puisque les deux vecteurs ne sont pas proportionnels l’un à l’autre, les lignes ne peuvent que se toucher ou se croiser. Par conséquent, nous devons maintenant résoudre le déterminant suivant formé par le vecteur directeur et un point de chaque droite :

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Nous substituons les valeurs dans la formule:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

Et nous calculons le déterminant, pour cela vous pouvez utiliser n’importe quelle méthode (règle de Sarrus, méthode des compléments ou des cofacteurs, etc.) :

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Si le résultat de la détermination avait été nul, cela signifierait que les lignes se croisent (elles se touchent). Mais le déterminant est différent de 0, donc les droites se coupent .

Trouver la position relative de deux lignes par rangs

Une autre façon de trouver la position relative de deux lignes consiste à calculer les rangs de deux matrices concrètes, comme nous le verrons ensuite. Cette méthode est très utile lorsque les deux lignes sont sous forme d’équation implicite (ou générale).

Donc, si on a deux droites exprimées avec leurs équations implicites (ou générales) dans un espace à trois dimensions (dans R3) :

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Soit A la matrice composée des coefficients des deux droites :

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

Et étant donné la matrice étendue A’, qui est la matrice formée par tous les paramètres des deux droites :

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Ensuite, la position relative des deux lignes peut être déterminée par la plage des deux matrices précédentes selon le tableau suivant :

positions relatives de deux lignes par rangs

Par conséquent, pour trouver la position relative entre deux lignes, nous devrons calculer les rangs des deux matrices et en fonction du rang de chaque matrice, ce sera un cas ou un autre.

Ce théorème peut être prouvé à partir du théorème de Rouché-Frobenius (une méthode utilisée pour résoudre des systèmes d’équations linéaires), cependant sur cette page nous ne ferons pas la preuve car elle est assez lourde et n’apporte pas grand chose.

Exemple de comment trouver la position relative de deux lignes par plages

Une fois que nous avons vu la théorie sur les positions relatives entre deux lignes par rangs, voyons comment elle est mise en pratique à travers un exemple :

Trouvez la position relative des deux lignes suivantes :

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

Les deux lignes se présentent sous la forme d’équations générales (ou implicites), nous utiliserons donc la méthode des rangs pour trouver la position relative entre les deux lignes. On construit donc la matrice A et la matrice étendue A’ avec les coefficients des droites :

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Une fois que nous avons les deux matrices, nous devons calculer le rang de chacune. On calcule d’abord le rang de la matrice A par déterminants :

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

La matrice A contient le déterminant d’une sous-matrice 3×3 non nulle, donc la matrice A est de rang 3 .

Et maintenant nous calculons la portée de la matrice étendue A’. La matrice A’ sera toujours au moins au rang de la matrice A, qui dans ce cas vaut 3, il suffit donc de vérifier si elle est de rang 4 ou de rang 3. Pour cela, on résout le déterminant de la matrice 4×4 par adjonctions (ou cofacteurs) :

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

Le déterminant de toute la matrice étendue est nul, donc la matrice A’ est également de rang 3 .

Donc la matrice A et la matrice A’ sont de rang 3 donc, par conséquent, les deux droites se coupent . C’est-à-dire qu’il n’y a qu’un seul point d’intersection entre eux.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Rappelons que vous avez ci-dessus un tableau qui résume tous les cas possibles des positions relatives entre deux droites selon les plages des matrices A et A’.

Problèmes résolus de la position relative entre deux lignes dans l’espace

Exercice 1

Trouvez la position relative entre les deux lignes suivantes :

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

voir solution

Puisque les deux lignes sont exprimées sous la forme d’une équation vectorielle, nous trouverons la position relative entre les deux lignes à partir de la méthode d’un point et d’un vecteur de chaque ligne.

Le vecteur directeur de chaque droite est :

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

Et un point qui appartient à chaque ligne est :

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Ainsi, pour appliquer la procédure, il faut d’abord vérifier si les composantes des vecteurs directeurs sont proportionnelles :

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

Étant donné que les deux vecteurs ne sont pas proportionnels l’un à l’autre, les lignes ne peuvent être que sécantes ou sécantes. Par conséquent, nous devons maintenant résoudre le déterminant suivant composé du vecteur directeur et d’un point de chaque droite :

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Nous substituons les valeurs dans la formule:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

Et on calcule le déterminant :

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

Le résultat du déterminateur est équivalent à 0, donc les droites se coupent .

Exercice 2

Calculez la position relative des deux lignes suivantes :

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

voir solution

La première ligne est sous la forme d’équations paramétriques et la deuxième ligne est sous la forme d’une équation continue, avec laquelle nous déterminerons la position relative entre les deux lignes à partir de la méthode d’un point et d’un vecteur de chaque ligne.

Les coordonnées du vecteur directeur de la droite

$r$ sont les coefficients devant le paramètre $t,$ et les coordonnées du vecteur directeur de la droite $s$ sont les nombres des dénominateurs :

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

Et un point qui appartient à chaque ligne est :

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

Ainsi, pour appliquer la procédure, il faut d’abord vérifier si les composantes des vecteurs directeurs sont proportionnelles :

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

Les deux vecteurs sont proportionnels l’un à l’autre, donc les droites ne peuvent être que parallèles ou coïncidentes. Pour lever ce doute, il faut substituer le point de la droite

$r$ dans l’équation de la droite $s$ (ou vice versa) pour voir si elle satisfait ladite équation :

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

En substituant le point dans la droite on obtient une égalité, de sorte que le point d’une droite vérifie l’équation de l’autre droite et, de plus, leurs vecteurs directeurs sont proportionnels. Par conséquent, les deux lignes coïncident.

Exercice 3

Trouvez la position relative des deux lignes suivantes :

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

voir solution

Les deux lignes sont sous forme d’équation générale (ou implicite), nous utiliserons donc la méthode des rangs pour trouver la position relative entre les deux lignes. On fait donc la matrice A et la matrice développée A’ avec les coefficients des droites :

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

Une fois que nous avons les deux matrices, nous devons calculer le rang de chacune. On calcule d’abord le rang de la matrice A par déterminants :

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

Tous les déterminants 3×3 de la matrice A sont nuls, mais il y a un déterminant 2×2 non nul à l’intérieur de la matrice, donc la matrice A est de rang 2 .

Et maintenant nous calculons la portée de la matrice étendue A’. La matrice A’ sera toujours au moins la plage de la matrice A, qui dans ce cas est 2, il faut donc vérifier si elle a un déterminant 3×3 qui ne s’annule pas et aussi combien vaut le déterminant de la matrice entière :

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

La matrice étendue A’ contient bien 3×3 sous-déterminants non nuls et, de plus, le déterminant de toute la matrice étendue est égal à 0, donc la matrice A’ a le rang 3 .

Donc la matrice A est de rang 2 et la matrice A’ est de rang 3, donc les deux droites sont parallèles . C’est-à-dire qu’ils n’ont rien en commun.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Rappelons que dans l’explication de la méthode (ci-dessus) vous avez un tableau qui résume tous les cas possibles des positions relatives entre deux lignes selon les rangs des matrices A et A’.

Exercice 4

Trouvez la position relative des deux lignes suivantes :

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

voir solution

Dans ce cas, les deux lignes sont sous forme d’équation cartésienne (ou implicite), nous allons donc utiliser la méthode de classement pour trouver la position relative entre les deux lignes. On construit donc la matrice A et la matrice étendue A’ avec les coefficients des droites :

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

Une fois que nous connaissons les deux matrices, nous devons calculer le rang de chacune. On va d’abord calculer le rang de la matrice A par déterminants :

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

La matrice A contient une sous-matrice 3×3 dont le déterminant est différent de zéro, donc la matrice A est de rang 3 .

Et maintenant nous calculons la portée de la matrice étendue A’. La matrice A’ sera toujours au moins de rang de la matrice A, qui dans ce cas vaut 3, il suffit donc de vérifier si elle est de rang 4 ou de rang 3. Pour ce faire, on résout le déterminant de l’ensemble de la matrice 4×4 par des adjonctions (ou cofacteurs) :

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

Le déterminant de toute la matrice étendue est non nul, donc la matrice A’ est de rang 4 .

Si bien que la matrice A est de rang 3 et qu’au contraire la matrice A’ est de rang 4, donc les deux droites se coupent en un point.

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Rappelons que dans l’explication de la procédure (ci-dessus) vous avez un tableau où se trouvent tous les cas possibles des positions relatives entre deux lignes selon les rangs des matrices A et A’.

Position relative de deux lignes dans l’espace

Quelles sont les positions relatives de deux droites dans l’espace ?

Détermination de la position relative de deux lignes à partir d’un point et d’un vecteur

Exemple de détermination de la position relative entre deux lignes

Trouver la position relative de deux lignes par rangs

Exemple de comment trouver la position relative de deux lignes par plages

Problèmes résolus de la position relative entre deux lignes dans l’espace

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Leave a Comment Cancel Reply