Dans cet article, nous allons passer en revue les concepts nécessaires pour comprendre ce qu’est un polynôme complet . De plus, nous apprendrons comment il est utilisé et pourquoi c’est une idée si importante pour la manipulation et la quantification des polynômes. Bien que, tout d’abord, il est fortement recommandé de lire notre article sur le polynôme .
Qu’est-ce qu’un polynôme complet ?
Un polynôme complet est une expression algébrique composée d’une somme de termes. Chaque terme est formé en multipliant un nombre, appelé coefficient, par une puissance de x. La puissance la plus élevée dans le polynôme est appelée le degré du polynôme, et la plus faible (x élevé à zéro) est appelée le terme indépendant.
À partir de là, nous définissons un polynôme complet comme celui qui comprend des termes de tous les degrés possibles jusqu’au degré du polynôme . En d’autres termes, si un polynôme a un degré de 5, alors il doit inclure des termes de degré 5, 4, 3, 2, 1 et 0. En d’autres termes, un polynôme complet est celui qui n’a pas de termes nuls (égal à zéro).
Dans l’image suivante, vous pouvez en voir un exemple. Comme on peut le voir, il a un terme pour chaque exposant de x, de x à la puissance quatre (quatre étant le degré du polynôme) à x à la puissance zéro, dans le terme indépendant. Par conséquent, ce polynôme répond à la définition d’un polynôme complet.
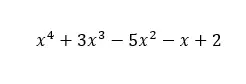
Par contre, si nous avons un autre polynôme comme celui de l’image suivante, nous aurons affaire à un polynôme incomplet . Puisqu’il manque deux termes, celui de x élevé à deux et le terme indépendant. Et à partir de la définition d’un polynôme complet, s’il manque même un terme, le polynôme n’est plus complet.
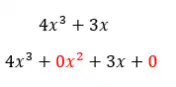
Exemples de polynômes complets
Maintenant que vous connaissez la définition du polynôme complet, voyons quelques exemples concrets . On va commencer par regarder un polynôme complet de degré 2, un autre de degré 4, et enfin un de degré 6. On pourrait évidemment donner des exemples de degrés beaucoup plus élevés, mais l’idée est la même avec tous les types de polynômes.
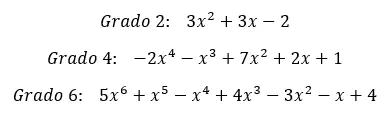
Avec ces exemples la définition des polynômes complets est très claire. C’est pourquoi nous pouvons maintenant passer au niveau suivant. Dans la section suivante nous détaillerons les deux types de polynômes complets qui existent, selon l’ordre des termes. C’est quelque chose que beaucoup d’étudiants tiennent pour acquis, mais il est bon de le revoir.
Types de polynômes complets
Nous pouvons classer les polynômes complets en deux types : les polynômes complets ordonnés et les polynômes complets non ordonnés ou non ordonnés. Les premiers sont caractérisés par une structure dont les termes sont ordonnés selon les degrés de x. Commençant par le diplôme le plus élevé et se terminant par le terme indépendant.
Bien qu’il s’agisse d’un polynôme complet non ordonné, il est exprimé avec les termes dans un ordre aléatoire . Par conséquent, vous pouvez trouver le terme avec le plus grand exposant à côté du terme indépendant. Mais, cette façon d’exprimer un polynôme n’est pas pratique, nous vous recommandons donc de toujours utiliser des polynômes ordonnés .
Ensuite, nous vous montrerons un exemple de chaque type, afin que vous puissiez bien apprécier la différence.
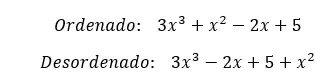
Nous espérons que cet article vous a aidé à comprendre le concept de polynômes complets. Si vous avez des questions, n’hésitez pas à les laisser dans les commentaires.