Points d'inflexion d'une fonction -

Nous expliquons ici ce qu’est un point d’inflexion d’une fonction et comment trouver tous les points d’inflexion d’une fonction. De plus, vous trouverez des exercices pas à pas sur la courbure et les points d’inflexion d’une fonction.

Quels sont les points d’inflexion d’une fonction ?

Les points d’inflexion d’une fonction sont les points auxquels le graphique de la fonction change de courbure, c’est-à-dire qu’à un point d’inflexion, une fonction passe de concave à convexe ou vice versa.

Comment savoir si une fonction a un point d’inflexion

Étant donné la définition du point d’inflexion, voyons comment savoir si un certain point est un point d’inflexion de la fonction.

Une fonction a un point d’inflexion aux points qui annulent sa dérivée seconde et sa dérivée troisième est non nulle.

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

A titre d’exemple, nous allons calculer les points d’inflexion de la fonction du troisième degré suivante :

$f(x)=x^3-5x$

Tout d’abord, on calcule les dérivées deuxième et troisième de la fonction :

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

Maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation résultante :

$6x=0$

$x=0$

Ensuite, le point x=0 sera un point d’inflexion de la fonction si la dérivée tierce est non nulle en ce point. Dans notre cas, la dérivée troisième est toujours égale à 6.

$f'''(0)=6\neq 0$

Par conséquent, x=0 est un point d’inflexion de la fonction.

Comment étudier la courbure et trouver les points d’inflexion d’une fonction

Nous venons de voir une méthode pour trouver des points tournants. Cependant, on a normalement tendance à étudier la courbure d’une fonction, c’est-à-dire à déterminer la concavité et la convexité d’une fonction, et à partir de là, à calculer les points d’inflexion.

Pour trouver les points d’inflexion d’une fonction à travers sa courbure, les étapes suivantes doivent être effectuées :

Trouvez les points qui n’appartiennent pas au domaine de la fonction.
Calculez la dérivée première et la dérivée seconde de la fonction.
Trouver les racines de la dérivée seconde , c’est-à-dire calculer les points qui annulent la dérivée seconde en résolvant $f''(x)=0$ .
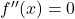Faites des intervalles avec les racines de la dérivée et les points qui n’appartiennent pas au domaine de la fonction.
Calculez la valeur de la dérivée seconde en un point de chaque intervalle.
Le signe de la dérivée seconde détermine la concavité ou la convexité de la fonction dans cet intervalle :
- Si la dérivée seconde de la fonction est positive, la fonction est convexe sur cet intervalle.
- Si la dérivée seconde de la fonction est négative, la fonction est concave sur cet intervalle.
Les points d’inflexion sont les points auxquels la fonction passe de convexe à concave ou vice versa.

Afin que vous puissiez voir comment les points d’inflexion d’une fonction sont calculés à l’aide de cette procédure, nous allons résoudre un exemple étape par étape ci-dessous :

Étudiez la courbure et trouvez les points d’inflexion de la fonction polynomiale suivante :

$f(x)=x^4-6x^2$

La première chose à faire est de calculer le domaine de définition de la fonction. C’est une fonction polynomiale, donc le domaine de la fonction est constitué de nombres réels, c’est-à-dire que c’est une fonction continue :

$\text{Dom } f= \mathbb{R}$

Une fois que nous avons calculé le domaine de la fonction, nous devons étudier à quels points elle est remplie

$f''(x)=0$ .

Nous calculons donc d’abord la dérivée première de la fonction :

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

Ensuite, nous calculons la dérivée seconde de la fonction :

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

Et maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation :

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

Une fois que nous avons calculé le domaine de la fonction et

$f''(x)=0$ , nous représentons tous les points critiques trouvés sur la droite numérique :

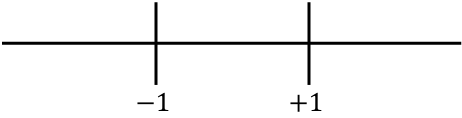
Et maintenant nous évaluons le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle (jamais les points critiques) et regardons quel signe la dérivée seconde a à ce point :

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.

$(\bm{\cup})$ , et si la dérivée seconde est négative cela signifie que la fonction est concave $(\bm{\cap})$ . Par conséquent, les intervalles de concavité et de convexité de la fonction sont :

Convexe

$(\bm{\cup})$ : $\bm{(-\infty,-1) \cup (1,+\infty)}$

Concave

$(\bm{\cap})$ : $\bm{(-1,1)}$

De plus, à x=-1 la fonction passe de convexe à concave, donc x=-1 est un point d’inflexion de la fonction . Et à x=1, la fonction passe de concave à convexe, donc x=1 est aussi un point d’inflexion de la fonction.

Enfin, nous substituons les points trouvés dans la fonction d’origine pour trouver la coordonnée Y des points d’inflexion :

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

Les tournants de la fonction sont donc :

Points tournants :

$\bm{(-1,-5)}$ et $\bm{(1,-5)}$

Ci-dessous vous pouvez voir la représentation graphique de la fonction étudiée :

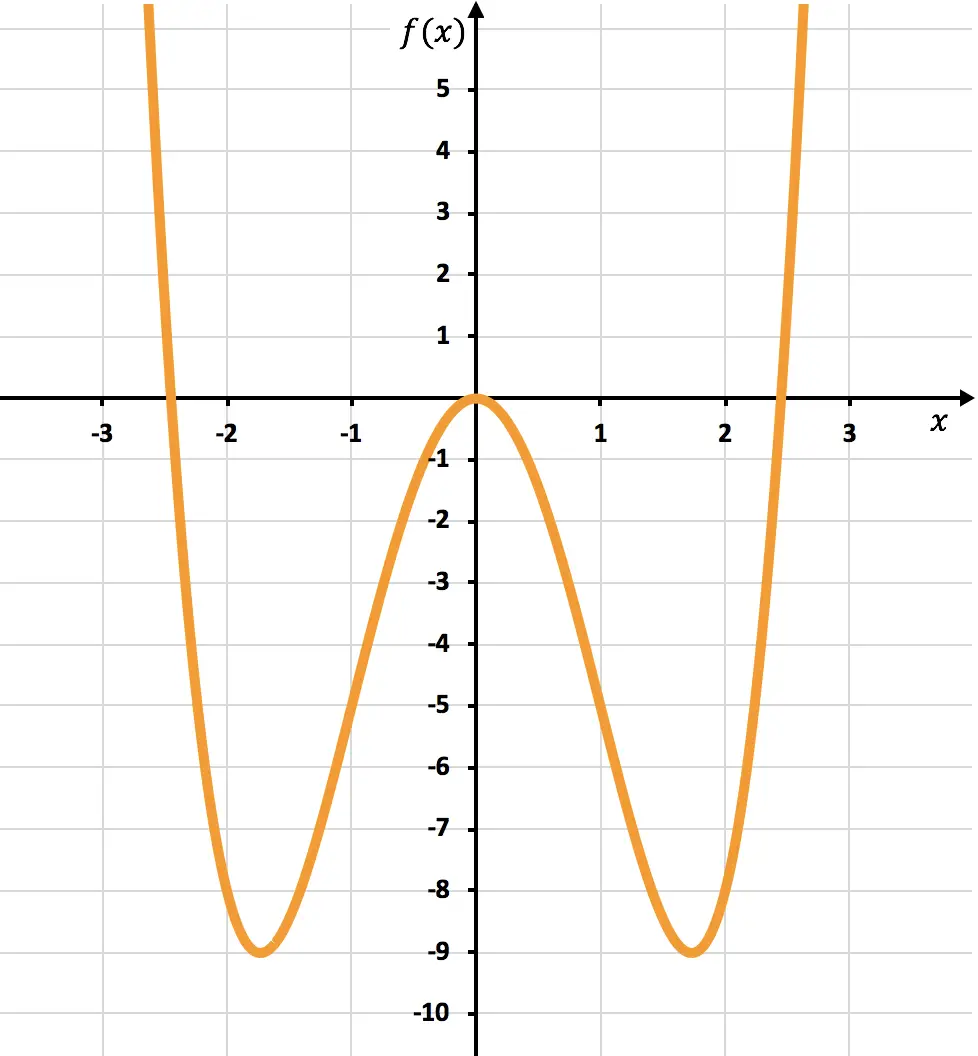
Comme vous pouvez le voir sur le graphique, la fonction passe de convexe

$(\cup)$ être concave $(\cap)$ Sur le point $(-1,-5)$ puisque sa courbure change. Et d’un autre côté, la fonction passe de concave $(\cap)$ être convexe $(\cup)$ Sur le point $(1,-5)$ .

Exercices de tournant résolus

Exercice 1

Calculez les intervalles de concavité et de convexité ainsi que les points d’inflexion de la fonction exponentielle suivante :

$f(x) = xe^x$

Voir la solution

La première chose à faire est de calculer le domaine de définition de la fonction. La fonction est composée d’une fonction polynomiale (x), dont le domaine est composé uniquement de nombres réels, et d’une fonction exponentielle (e ^x ), dont le domaine est également constitué de nombres réels. Par conséquent, le domaine de la fonction est constitué de nombres réels :

$\text{Dom } f= \mathbb{R}$

Calculons maintenant la dérivée de la fonction. Dans ce cas, la fonction est composée du produit de deux fonctions, donc pour dériver la fonction, nous devons appliquer la formule de la dérivée d’un produit :

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

Ensuite, nous calculons la dérivée seconde de la fonction :

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

Nous fixons la dérivée seconde égale à 0 et résolvons l’équation :

$f''(x)= 0$

$2e^x+xe^x= 0$

On extrait le facteur commun :

$e^x(2+x)=0$

Pour que la multiplication soit égale à 0, il faut qu’un des deux éléments de la multiplication soit nul. Par conséquent, nous fixons chaque facteur égal à 0 :

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

Un nombre élevé à un autre ne peut jamais donner 0. Par conséquent, l’équation

$e^x=0$ Il n’y a pas de solution.

On représente tous les points singuliers obtenus sur la droite :

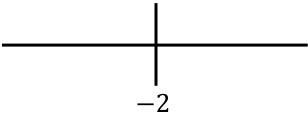
Et maintenant nous évaluons le signe de la dérivée seconde dans chaque intervalle pour savoir si la fonction est concave ou convexe. Pour ce faire, nous prenons un point dans chaque intervalle et regardons quel signe a la dérivée seconde à ce point :

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.

$(\bm{\cup})$ , et si la dérivée seconde est négative cela signifie que la fonction est concave $(\bm{\cap})$ . Les intervalles de concavité et de convexité sont donc :

Convexe

$(\bm{\cup})$ : $\bm{(-2,+\infty)}$

Concave

$(\bm{\cap})$ : $\bm{(-\infty,-2)}$

De plus, la fonction passe de concave à convexe en x=-2, donc x=-2 est un point d’inflexion de la fonction.

Enfin, nous substituons le point d’inflexion trouvé dans la fonction d’origine pour trouver la coordonnée Y du point :

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

En conclusion, les seuls tournants de la fonction sont :

Points tournants :

$\bm{(-2,-2e^{-2})}$

Exercice 2

Étudiez les intervalles de concavité et de convexité et trouvez les points d’inflexion de la fonction rationnelle suivante :

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Voir la solution

Nous devons d’abord calculer le domaine de la fonction. Puisqu’il s’agit d’une fonction rationnelle, nous mettons le dénominateur égal à zéro pour voir quels nombres n’appartiennent pas au domaine de la fonction :

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Cela signifie que lorsque x vaut -2 ou +2, le dénominateur sera 0. Et par conséquent, la fonction n’existera pas. Le domaine de la fonction est donc composé de tous les nombres sauf x=-2 et x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Deuxièmement, nous calculons la dérivée première de la fonction :

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Et puis on résout la dérivée seconde :

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Tous les termes sont multipliés par

$(x^2-4)$ . On peut donc simplifier la fraction :

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Calculons maintenant les racines de la dérivée seconde de la fonction :

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Le terme

$\left(x^2-4\right)^3$ Il s’agit de diviser tout le côté gauche, nous pouvons donc le multiplier par tout le côté droit :

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

On extrait le facteur commun :

$x(8x^2+96)=0$

Pour que la multiplication soit égale à 0, il faut qu’un des deux éléments de la multiplication soit nul. Par conséquent, nous fixons chaque facteur égal à 0 :

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$ Il n’y a pas de solution puisqu’il n’existe pas de racine négative d’un nombre réel.

Nous représentons maintenant sur la ligne tous les points critiques obtenus, c’est-à-dire les points qui n’appartiennent pas au domaine (x=-2 et x=+2) et ceux qui annulent la dérivée seconde (x=0) :

Et on évalue le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle et regardons quel signe a la dérivée seconde à ce point :

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.

$(\bm{\cup})$ , et si la dérivée seconde est négative cela signifie que la fonction est concave $(\bm{\cap})$ . Les intervalles de concavité et de convexité sont donc :

Convexe

$(\bm{\cup})$ : $\bm{(-2,0)\cup (2,+\infty)}$

Concave

$(\bm{\cap})$ : $\bm{(-\infty,-2)\cup (0,2)}$

La fonction change de courbure en trois points, par conséquent, la fonction rationnelle aurait en principe trois points d’inflexion, qui sont x=-2, x=0 et x=2. Cependant, bien qu’il y ait un changement de courbure à x=-2 et à x=+2, ce ne sont pas des points d’inflexion car ils n’appartiennent pas au domaine de la fonction. D’un autre côté, à x=0 il y a un changement de courbure et cela appartient à la fonction, donc x=0 est le seul point d’inflexion de la fonction.

Il ne reste plus qu’à calculer la coordonnée Y du point d’inflexion :

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$

Bref, le seul point d’inflexion de la fonction rationnelle est l’origine des coordonnées :

Points tournants :

$\bm{(0,0)}$

Exercice 3

On sait que la fonction

$f(x)=x^3+ax^2+bx+c$ passer par le point $(3,1)$ , a un extrême relatif dans $x=1$ , et un tournant dans $x = 2$ . À partir de ces informations, calculez les valeurs des paramètres $a, b$ et $c$ .