Cette page explique quels sont les points d’intersection (ou croisement) d’une fonction avec les axes cartésiens et comment les calculer. De plus, vous trouverez plusieurs exemples pour bien comprendre comment ils se trouvent et vous pourrez même vous entraîner avec des exercices résolus étape par étape.
Quels sont les points d’intersection (ou d’intersection) d’une fonction avec les axes ?
Avant de voir comment ils sont calculés, rappelons quels sont les points d’intersection d’une fonction avec les axes.
Les points d’intersection ou d’intersection avec les axes sont les points où la représentation d’une fonction coupe les axes de coordonnées, c’est-à-dire les points du graphique qui se trouvent sur l’axe X et sur l’axe Y.
Par exemple, la parabole dans le graphique suivant coupe l’axe Y au point (0,3) et coupe l’axe X aux points (-1,0) et (3,0).
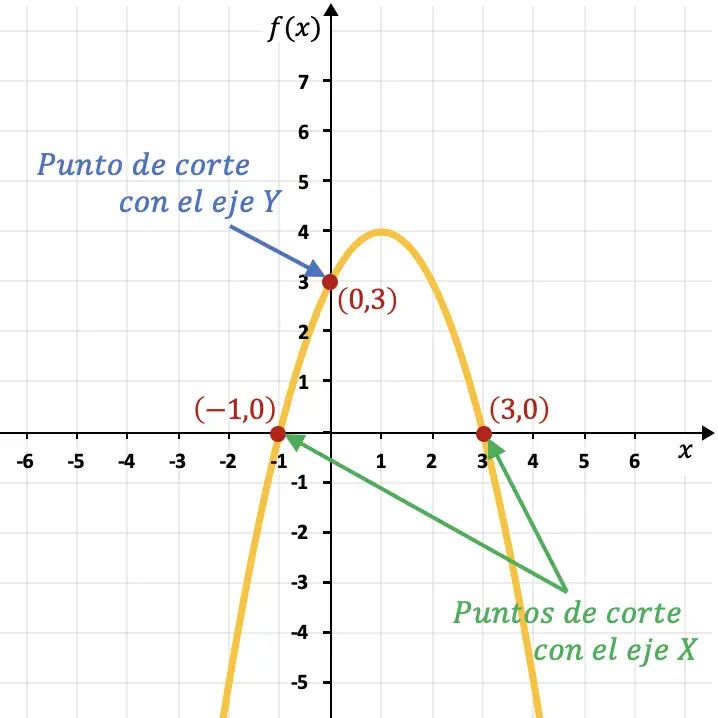
Point de coupure d’une fonction avec l’axe X
La deuxième coordonnée des points d’intersection d’une fonction avec l’axe X sera toujours 0, donc :
Les points de coupure de toute fonction d’axe des abscisses OX sont de la forme
, et peut être calculé en résolvant l’équation suivante :
Parfois, lors de la résolution de cette équation, nous pouvons obtenir deux (ou plus) solutions, cela signifie que la fonction coupe l’axe X deux (ou plus) fois. En revanche, si l’équation n’a pas de solution, cela implique que la fonction ne coupe pas l’axe X.
Point de coupure d’une fonction avec l’axe Y
La première coordonnée des points d’intersection d’une fonction avec l’axe Y sera toujours 0, donc :
Le point de coupure de toute fonction avec l’axe des ordonnées OY est de la forme
, et peut être trouvé en calculant l’image de la fonction à x=0 :
Contrairement aux points d’arrêt sur l’axe X, il ne peut y avoir qu’un seul point d’arrêt sur l’axe Y.
Exemple de calcul des points de coupure d’une fonction avec les axes
Pour que vous n’ayez aucun doute, nous allons voir ci-dessous un exemple de comment trouver les points de coupure d’une fonction avec les axes cartésiens :
- Trouvez numériquement les points de coupure de la fonction suivante :
Nous allons d’abord calculer le point de coupure de la fonction avec l’axe des abscisses. Le point d’intersection avec l’axe X aura toujours la deuxième composante égale à 0, c’est-à-dire qu’il sera du type
. Parce que f(x) est toujours égal à 0 sur l’axe OX. Donc, pour trouver l’autre composante du point, nous devons résoudre l’équation 
Le point d’intersection avec l’axe X est donc :
Nous allons maintenant trouver le point d’intersection avec l’axe des ordonnées. Le point d’intersection avec l’axe Y aura toujours la première composante égale à 0, c’est-à-dire que le point sera du type
. Puisque la variable indépendante x s’annule toujours sur l’axe Y. Donc, pour trouver l’autre coordonnée du point, nous devons calculer
Le point d’intersection avec l’axe Y est donc :
Ci-dessous vous avez l’exemple de fonction représenté graphiquement, vous pouvez voir que les seuils trouvés coïncident avec ceux du graphique :
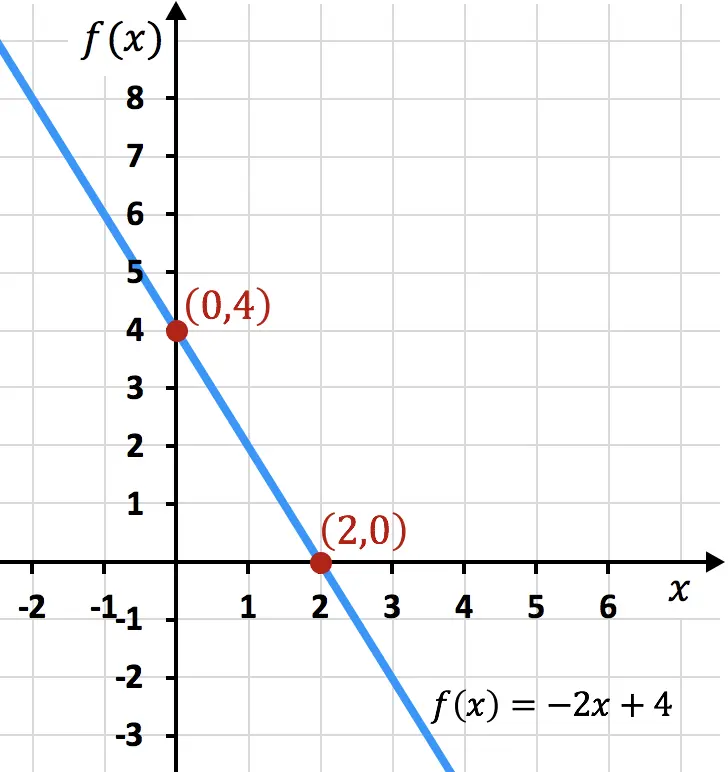
Exercices résolus de points de coupure d’une fonction avec les axes
Exercice 1
Déterminez les points de coupe avec les axes de coordonnées de la fonction suivante :
Point de coupe avec l’axe X
Pour trouver le point d’intersection de la fonction avec l’axe X il faut résoudre
Le point d’intersection de la fonction avec l’axe X est donc :
Point de coupe avec l’axe Y
Pour trouver le point d’intersection avec l’axe Y il faut calculer
Le point d’intersection de la fonction avec l’axe Y est donc :
Exercice 2
Trouver les points d’intersection avec les axes cartésiens de la fonction affine suivante :
Point de coupe avec l’axe X
Pour trouver le point limite de la fonction avec l’axe OX, nous devons mettre la fonction égale à zéro et résoudre l’équation résultante :
Donc le point d’intersection de la fonction avec l’axe des abscisses est :
Point de coupe avec l’axe Y
Pour trouver le point de coupure avec l’axe OY, nous devons calculer
Le point d’intersection de la fonction avec l’axe des ordonnées est donc :
Exercice 3
Calculez les points de coupure avec les axes de la fonction quadratique suivante :
Point de coupe avec l’axe X
Pour trouver le point d’intersection de la fonction avec l’axe X il faut résoudre
Dans ce cas, nous devons résoudre une équation du deuxième degré, nous appliquons donc la formule :
![\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47048fdd48ce98ba99629edf5a379f76_l3.png "Rendered by QuickLaTeX.com")
Nous avons obtenu deux solutions de l’équation quadratique, donc la fonction coupe l’axe X en deux points :
Point de coupe avec l’axe Y
Par contre, pour déterminer le point d’intersection avec l’axe Y, il faut calculer
Par conséquent, le seul point d’intersection de la fonction avec l’axe Y est :
Exercice 4
Trouver les points d’intersection avec les axes du plan cartésien de la fonction rationnelle suivante :
Point de coupe avec l’axe X
Pour trouver le point d’intersection de la fonction avec l’axe X il faut résoudre
5 n’est pas équivalent à 0, donc l’équation n’a pas de solution et, par conséquent, il n’y a pas de point d’intersection entre la fonction et l’axe X.
Point de coupe avec l’axe Y
Pour trouver le point d’intersection avec l’axe Y il faut calculer
Tout nombre divisé par zéro est une indétermination qui donne l’infini. Par conséquent, la fonction ne dépasse en aucun point l’axe Y.
En bref, la fonction d’exercice n’a aucun point d’intersection avec les axes , c’est-à-dire que son graphique ne passe à aucun moment par l’axe X ou l’axe Y.
Exercice 5
Calculez les points de coupure avec les axes de la fonction de troisième degré suivante :
Point de coupe avec l’axe X
Pour trouver le point d’intersection de la fonction avec l’axe X il faut résoudre
Les deux termes de l’équation ont un x , avec lequel on peut extraire un facteur commun :
Pour que l’égalité précédente soit remplie, l’un des facteurs doit être 0. Par conséquent, nous fixons chaque facteur égal à zéro pour obtenir toutes les solutions possibles :
![\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37febaed85a502533604305b9009611d_l3.png "Rendered by QuickLaTeX.com")
Nous avons donc obtenu trois solutions de l’équation du troisième degré, donc la fonction coupe l’axe X en 3 points :
Point de coupe avec l’axe Y
Pour calculer le point de coupure avec l’axe Y, vous devez calculer
Par conséquent, le seul point d’intersection de la fonction avec l’axe Y est l’origine des coordonnées (0,0) :
Notez que nous avions déjà trouvé ce point dans le calcul du point de coupe avec l’axe X, car la fonction coupe à ce point avec les deux axes en même temps.