▷ Comment savoir si 3 (ou plus) points sont alignés ? ✅

Sur cette page, vous trouverez l’explication de ce que sont les points alignés. Vous verrez également toutes les méthodes disponibles pour déterminer si 3 points (ou plus) sont alignés. Et en plus, vous trouverez plusieurs exemples et même des exercices résolus pour que vous puissiez vous entraîner.

Qu’est-ce que cela signifie que les points sont alignés ?

En géométrie analytique, trois points ou plus sont alignés s’ils sont tous sur la même ligne, c’est-à-dire s’ils peuvent être joints en traçant une ligne droite entre eux.

Évidemment, 2 points seront toujours alignés, puisque vous pouvez toujours tracer une ligne entre deux points. Cependant, trois points ne doivent pas nécessairement être sur la même ligne. Principalement, il existe deux méthodes pour savoir si 3 points ou plus sont alignés :

Méthode vectorielle : consiste à voir si les vecteurs qui forment les points sont proportionnels.
Méthode d’équation de ligne : elle consiste à déterminer si les points appartiennent à la même ligne.

Vous trouverez ci-dessous l’explication de chaque procédure et des exemples afin que vous puissiez décider laquelle vous convient le mieux.

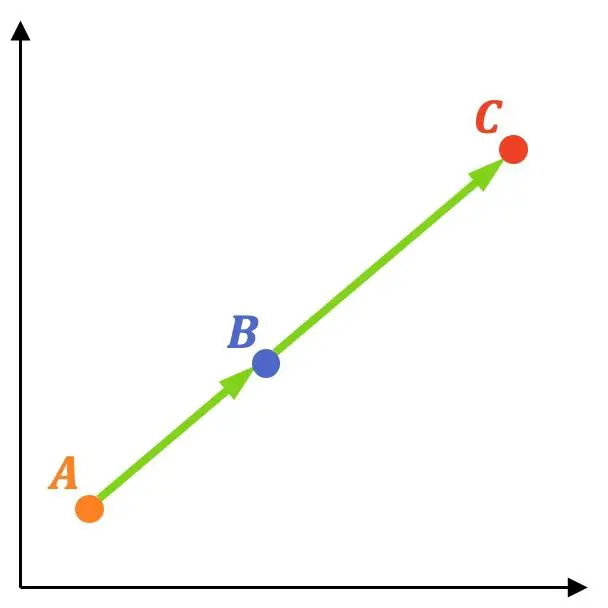
Comment savoir si 3 points (ou plus) sont alignés avec la méthode vectorielle

Compte tenu de trois points :

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Les trois points sont alignés si les vecteurs

$\vv{AB}$ et $\vv{BC}$ ils ont la même direction, c’est-à-dire si leurs composantes sont proportionnelles.

Voyons un exemple de la façon dont cela se fait :

Déterminez si les 3 points suivants sont alignés :

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Tout d’abord, nous calculons les vecteurs entre les points. Il suffit de calculer deux vecteurs différents :

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

Et puis on vérifie si les coordonnées des vecteurs sont proportionnelles :

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

En divisant les composantes X et les composantes Y des deux vecteurs on obtient le même résultat (-2), donc les vecteurs ont la même direction et, par conséquent, les points sont alignés .

Cette méthode peut également être utilisée pour savoir si trois points ou plus sont alignés dans l’espace (dans R3), la seule chose qu’il faut ajouter est de vérifier que la troisième composante des deux vecteurs (composante Z) est également proportionnelle.

Si cet article vous est utile, vous serez probablement aussi intéressé de savoir comment calculer le milieu entre deux points , puisque, évidemment, trouver le milieu de 2 points est un moyen de déterminer un troisième point aligné avec les deux autres points. Vous pouvez voir comment cela se fait sur la page liée, en plus, vous pourrez également voir des exemples et des exercices résolus étape par étape.

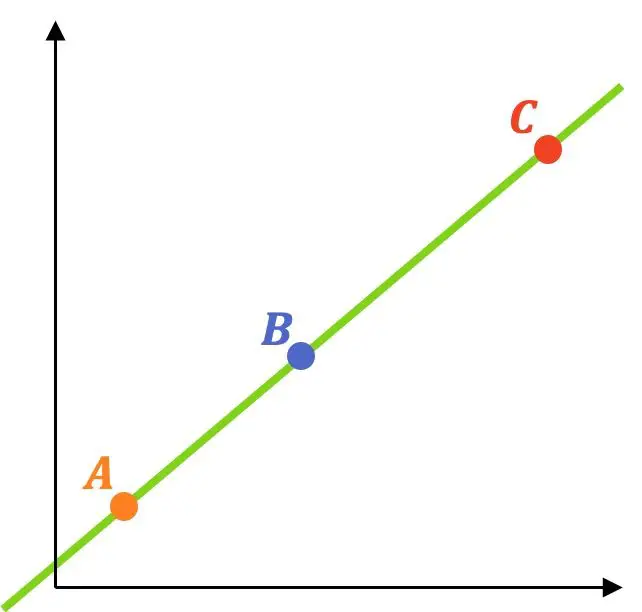
Comment savoir si 3 points (ou plus) sont alignés avec la méthode de l’équation en ligne droite

Comme nous venons de le voir dans la section précédente, une façon d’étudier l’alignement de 3 points ou plus consiste à utiliser les vecteurs qui peuvent se former entre eux. Eh bien, une autre méthode consiste à partir de l’équation d’une droite :

Compte tenu de trois points :

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Les trois points sont alignés s’ils appartiennent tous à la même droite. Par conséquent, pour savoir si trois points ou plus sont alignés, les étapes suivantes doivent être suivies :

Trouvez l’équation de la droite qui passe par deux des trois points.
Vérifiez si le troisième point appartient également à la ligne. Dans ce cas cela signifie que les 3 points sont alignés, par contre si la condition n’est pas remplie cela signifie que les points ne sont pas alignés.

A titre d’exemple, nous allons résoudre un exercice en utilisant cette méthode :

Vérifiez que les 3 points suivants sont alignés :

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Tout d’abord, il faut calculer l’équation de la droite qui passe par les points A et B. On trouve donc le vecteur direction de la droite :

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Maintenant il faut construire l’équation de la droite, vous pouvez choisir le type que vous voulez : paramétrique, implicite, générale, etc. Mais dans ce cas nous utiliserons l’équation continue. Ainsi l’équation continue de la droite qui passe par le point A et le point B sera :

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Une fois que l’on a l’équation de la droite, il faut vérifier si l’autre point appartient également à la même droite. Pour ce faire, on substitue les coordonnées du point C dans l’équation de la droite :

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

Nous avons obtenu une égalité, de sorte que le point satisfait l’équation de la droite. Et donc les 3 points sont colinéaires .

Il convient de noter qu’un ensemble de points alignés ne doit pas nécessairement être équidistant, c’est-à-dire que la distance entre plusieurs points alignés peut être différente. Vous pouvez voir la différence entre les deux concepts dans l’explication de la distance entre deux points (géométrie) , où vous pouvez également voir des exemples et des exercices résolus étape par étape.

Exercices résolus de points alignés

Exercice 1

Déterminez si les 3 points suivants sont alignés :

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Voir la solution

Nous pouvons choisir l’une des deux méthodes que nous avons vues pour résoudre le problème. Dans ce cas, nous utiliserons la méthode vectorielle.

Tout d’abord, on calcule les vecteurs entre les points :

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

Et maintenant on vérifie si les coordonnées cartésiennes des vecteurs sont proportionnelles :

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

En divisant les composantes X et les composantes Y des deux vecteurs l’une par l’autre on obtient le même résultat (-4), donc les vecteurs ont la même direction. Fait qui indique que les points sont alignés .

Exercice 2

Étant donné 3 points :

$A(6,3) \quad B(4,-3) \quad C(4,5)$

Déterminez lesquels sont alignés sur les deux points suivants :

$D(3,-1) \quad E(2,1)$

Voir la solution

Dans ce cas, nous utiliserons la méthode de l’équation en ligne droite, nous enregistrerons ainsi certains calculs.

On calcule donc l’équation continue de la droite qui passe par les points D et E :

$\vv{DE} = E-D = (2,1) - (3,-1) = (-1,2)$

$\cfrac{x-3}{-1}=\cfrac{y+1}{2}$

Et maintenant, vérifions quels points correspondent à l’équation de la droite, et sont donc alignés avec les points D et E, et lesquels ne le sont pas.

On vérifie le point A :

$\cfrac{6-3}{-1}=\cfrac{3+1}{2}$

$\cfrac{3}{-1}=\cfrac{4}{2}$

$-3\neq 2$

L’équation de la droite n’est pas vraie, donc le point A n’est pas aligné avec les points D et E.

Nous vérifions maintenant le point B :

$\cfrac{4-3}{-1}=\cfrac{-3+1}{2}$

$\cfrac{1}{-1}=\cfrac{-2}{2}$

$-1= -1$

Dans ce cas l’équation de la droite est remplie, donc le point B est colinéaire aux points D et E.

Et enfin, on répète le processus avec le point C :

$\cfrac{4-3}{-1}=\cfrac{5+1}{2}$

$\cfrac{1}{-1}=\cfrac{6}{2}$

$-1\neq 3$

L’équation de la droite n’est pas vraie, donc le point C n’est pas aligné avec les points D et E.

Exercice 3

Trouver la valeur de l’inconnu

$k$ pour que les 3 points suivants soient alignés :

$A(k,5) \quad B(-1,-4) \quad C(k-1,2)$

Voir la solution

Dans ce cas, nous utiliserons la méthode vectorielle.

On essaie donc de calculer les vecteurs entre les points :

$\vv{AB} = B - A = (-1,-4)- (k,5) = (-1-k,-9)$

$\vv{BC} = C-B =(k-1,2)- (-1,-4)= (k,6)$

Pour que la colinéarité en trois points soit satisfaite, les coordonnées des deux vecteurs doivent être proportionnelles. On applique donc cette condition :

$\cfrac{-1-k}{k} = \cfrac{-9}{6}$