Sur cette page vous trouverez ce que sont les plans perpendiculaires, comment déterminer si deux plans sont perpendiculaires, comment calculer un plan perpendiculaire, des exemples et des exercices résolus de plans perpendiculaires,…
Que sont deux plans perpendiculaires ?
En géométrie analytique, deux plans sont perpendiculaires lorsqu’ils se coupent à angle droit (90º).
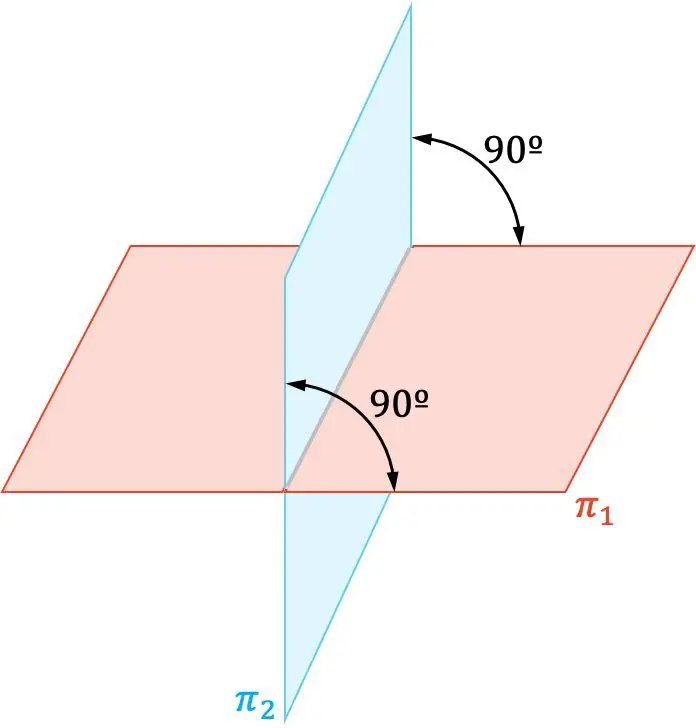
De plus, les vecteurs normaux de deux plans perpendiculaires sont également orthogonaux entre eux.
Évidemment, la distance entre deux plans perpendiculaires est toujours nulle, car ils se coupent en ligne. Bien que cela semble très simple, le concept de distance entre deux avions est très important, nous vous recommandons donc de visiter le lien si vous avez des questions à ce sujet.
D’autre part, deux plans positionnés perpendiculairement ne sont pas la seule position relative possible entre les plans, puisque deux plans dans l’espace (dans R3) peuvent également être sécants, parallèles ou coïncidents.
Comment savoir si un plan est perpendiculaire à un autre ?
Une fois que nous avons vu la définition des plans perpendiculaires, voyons comment savoir si deux plans sont perpendiculaires ou non :
Deux plans sont perpendiculaires lorsque leurs vecteurs normaux sont perpendiculaires. Par conséquent, pour déterminer si deux plans sont perpendiculaires l’un à l’autre, il faut calculer l’angle formé par leurs vecteurs normaux, et si ceux-ci forment un angle de 90º, cela signifie que les plans sont perpendiculaires.
Donc pour trouver la perpendicularité de deux plans il faut savoir calculer l’angle entre deux vecteurs . Si vous ne vous souvenez pas comment le faire, vous pouvez consulter le lien, où vous trouverez notre explication ainsi que la formule nécessaire pour déterminer l’angle entre deux vecteurs. De plus, vous pourrez voir des exemples et pratiquer avec des exercices résolus.
Mais en bref, deux vecteurs sont perpendiculaires lorsque leur produit scalaire est égal à zéro. Par conséquent, deux plans seront perpendiculaires lorsque le produit scalaire de leurs vecteurs normaux associés est égal à 0.
Exemple de deux plans perpendiculaires
Par exemple, vérifions si les deux plans suivants sont perpendiculaires :
Les coordonnées X, Y, Z du vecteur normal à un plan coïncident avec les coefficients A, B, C de son équation générale (ou implicite). Par conséquent, le vecteur normal à chaque plan est :
Et maintenant, nous vérifions s’il s’agit de deux plans perpendiculaires en calculant le produit scalaire entre leurs vecteurs normaux :
![\begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94cfcef6a93720224eff0bd4891839ed_l3.png "Rendered by QuickLaTeX.com")
Le produit scalaire entre les deux vecteurs normaux est égal à 0, donc les deux plans sont perpendiculaires l’un à l’autre.
Calculer un plan perpendiculaire à une droite en un point
Un problème typique des plans et des droites est de trouver l’équation d’un plan perpendiculaire à une droite en un point donné. Donc, ensuite, nous allons voir comment il est résolu au moyen d’un exemple :
- Trouver l’équation du plan perpendiculaire à la droite.
Sur le point
étant dit droite et point :
![\displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ac7260ee9792daec4f32e1f200df01b_l3.png "Rendered by QuickLaTeX.com")
Premièrement, nous devons trouver le vecteur normal au plan en question. et comme la ligne droite
est perpendiculaire au plan, son vecteur normal coïncidera avec le vecteur directeur de la droite.
Dans ce cas, la ligne
est sous la forme d’équations paramétriques, donc les composantes de son vecteur directeur sont les termes devant le paramètre
Ainsi, le vecteur normal au plan sera le même que le vecteur directeur de la droite :
Et, par conséquent, l’équation implicite (ou générale) du plan sera la suivante :
Il suffit donc de déterminer la valeur du coefficient D. Pour ce faire, on substitue les coordonnées du point dont l’énoncé nous dit qu’il appartient au plan dans son équation :
En bref, l’équation cartésienne du plan est :
En revanche, si vous souhaitez vous entraîner avec plus d’exercices sur la perpendicularité entre objets géométriques, vous pouvez visiter notre page sur les droites perpendiculaires. Vous y trouverez tout ce qu’il faut savoir sur les droites perpendiculaires : quand deux droites sont perpendiculaires, comment calculer une perpendiculaire à une autre, des exemples, des exercices résolus et bien plus encore.
Propriétés des plans perpendiculaires
Tous les plans perpendiculaires ont les caractéristiques suivantes :
- Relation symétrique : Si un plan est perpendiculaire à un autre plan, ce plan est également perpendiculaire au premier plan. Cette propriété est également détenue par des plans parallèles.
- Propriété non réflexive : Évidemment, aucun plan ne peut être perpendiculaire à lui-même.
- Théorème : Dans l’espace tridimensionnel (3D), toute paire de plans perpendiculaires à un troisième plan doit nécessairement être parallèle. Autrement dit, si un plan est perpendiculaire à un autre plan et que ce plan est également perpendiculaire à un troisième plan, les premier et dernier plans sont parallèles entre eux.