Sur cette page vous trouverez tout sur les plans parallèles : lorsque deux plans sont parallèles, les équations de deux plans parallèles, des exemples, des exercices résolus, des propriétés,…
Que sont deux plans parallèles ?
En géométrie analytique, deux plans sont parallèles lorsqu’ils sont toujours à la même distance l’un de l’autre. Par conséquent, deux plans parallèles ne se coupent jamais et n’ont aucun point en commun.

Deux plans positionnés parallèlement ne sont pas la seule position relative possible entre les plans, puisque deux plans dans l’espace (dans R3) peuvent également être sécants ou coïncidents.
Comment savoir si deux plans sont parallèles ?
Après avoir vu la définition des plans parallèles, voyons comment vous pouvez déterminer si deux plans sont parallèles ou non.
Partant de l’équation générale (ou implicite) de deux plans différents :
![]()
![]()
Les 2 plans seront parallèles si leurs coefficients A, B et C sont proportionnels entre eux et non au coefficient D. Autrement dit, le parallélisme entre deux plans se produit lorsque l’équation suivante est remplie :
![]()
Exemple de deux plans parallèles
Par exemple, les deux plans suivants sont parallèles :
![]()
![]()
Les plans sont parallèles car les coefficients des variables X, Y, Z sont proportionnels entre eux, mais pas aux termes indépendants :
![]()
Calculer la distance entre deux plans parallèles
Deux plans parallèles sont toujours à la même distance, par conséquent , pour trouver la distance entre deux plans parallèles, nous pouvons prendre un point sur l’un des deux plans et calculer la distance de ce point à l’autre plan. Par conséquent, pour calculer la distance entre 2 plans parallèles, il est nécessaire de connaître la formule de la distance d’un point à un plan .

C’est une méthode pour trouver la distance entre deux plans parallèles. Cependant, il existe un moyen encore plus simple de le faire lorsque les coefficients A, B et C des équations des deux plans coïncident :
Soit les équations générales (ou implicites) de deux plans parallèles :
![]()
La formule pour calculer la distance entre deux plans parallèles est :
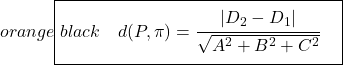
Alors surement il est plus facile de trouver la distance entre deux plans parallèles en utilisant la formule puisqu’il ne s’agit que d’appliquer la formule et c’est tout, mais cela dépend du problème. De plus, nous pensons qu’il est préférable d’expliquer les deux façons de calculer la distance afin que vous puissiez choisir celle que vous préférez.
Exemple de calcul de la distance entre deux plans parallèles
A titre d’exemple, nous allons calculer la distance entre les deux plans suivants :
![]()
Il faut d’abord vérifier qu’on a bien affaire à deux plans parallèles. Ainsi, tous les coefficients des équations des plans sont proportionnels sauf les termes indépendants, ce sont donc effectivement deux plans parallèles.
![]()
Dans ce cas, les termes A, B et C des équations des deux plans ne coïncident pas, mais on peut y parvenir en divisant par deux l’équation entière du second plan :
![]()
![]()
Ainsi, les équations des deux plans ont maintenant les mêmes coefficients A, B et C. Par conséquent, nous pouvons facilement calculer la distance entre les deux plans avec la formule de la distance entre deux plans parallèles :
![]()
Nous substituons les valeurs et résolvons les opérations:
![]()
De sorte que la distance entre un plan et l’autre plan est égale à l’unité.
Propriétés des plans parallèles
Les caractéristiques des plans parallèles sont les suivantes :
- Propriété réflexive : Chaque plan est parallèle à lui-même.
![]()
- Propriété symétrique : Si un plan est parallèle à un autre, ce plan est également parallèle au premier. Cette propriété est également possédée par les plans perpendiculaires.
![]()
- Propriété transitive : si un plan est parallèle à un autre plan, et que ce deuxième plan est parallèle à un troisième plan, le premier plan est également parallèle au troisième plan.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3](https://mathority.org/wp-content/ql-cache/quicklatex.com-cbdb26cf7c9104ca3111695826de0161_l3.png)