Sur cette page, vous trouverez l’explication la plus détaillée sur la pente d’une droite : quelle est sa formule, des exemples de calcul, ce que signifie le concept de pente d’une droite,… Vous pourrez également voir comment identifier facilement la pente d’une droite à partir de son équation et, en plus, vous pourrez vous entraîner avec des exercices résolus pas à pas.
Formule pour la pente d’une droite
La pente d’une droite est égale au déplacement vertical entre deux points divisé par le déplacement horizontal entre ces deux mêmes points.
C’est-à-dire, étant donné deux points sur une droite :
![]()
La formule de la pente d’une droite est :
![]()
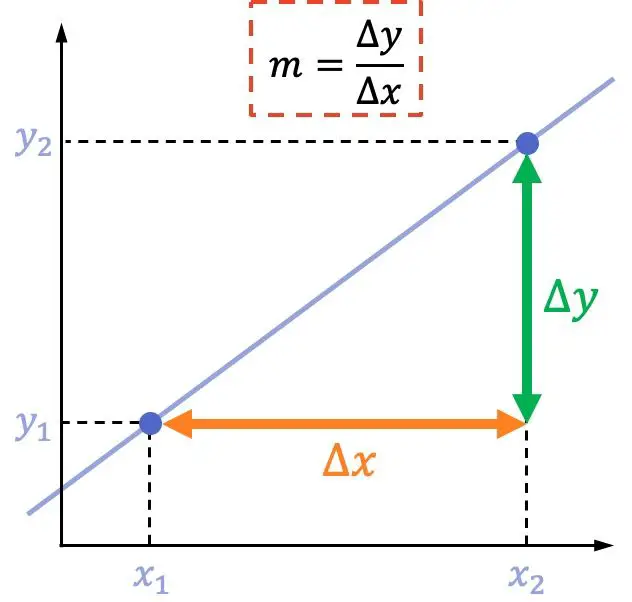
Exemple de calcul de la pente d’une droite à partir de deux points
Ensuite, nous verrons un exemple de la façon dont la pente d’une ligne est calculée avec la formule :
- Calculez la pente de la droite qui passe par les deux points suivants :
![]()
Pour trouver la pente de cette droite, il suffit d’appliquer sa formule :
![]()
La pente de la droite est donc égale à 3.
Trouver la pente d’une droite à partir de son équation
Dans la section ci-dessus, nous venons de voir comment déterminer numériquement la pente d’une droite. Cependant, il n’est pas toujours nécessaire de faire des calculs, mais sa valeur peut également être identifiée à partir de l’équation d’une ligne. Chaque type d’équation est différent, nous allons donc analyser chaque cas séparément.
Pente compte tenu de l’équation explicite de la ligne
L’équation explicite de la droite suit l’expression suivante :
![]()
Alors le paramètre
![]() correspond à la pente de la droite.
correspond à la pente de la droite.
Pente étant donné l’équation point-pente de la ligne
La formule de l’équation point-pente de la droite est la suivante :
![]()
Comme précédemment, le coefficient
![]() correspond à la pente de la droite.
correspond à la pente de la droite.
Pente compte tenu de l’équation implicite de la ligne
Étant donné l’équation implicite de la ligne (également appelée équation générale ou cartésienne):
![]()
La pente de la droite peut être trouvée en faisant :
![]()
Pente compte tenu du vecteur directeur de la ligne
Le vecteur directeur de la droite est le vecteur qui marque sa direction. Donc, si le vecteur directeur d’une droite est :
![]()
La pente de cette droite vaut :
![]()
pente donnée un angle
Enfin, si une droite forme un angle
![]() à la partie positive de l’axe des abscisses (axe X), sa pente est équivalente à la tangente de l’angle :
à la partie positive de l’axe des abscisses (axe X), sa pente est équivalente à la tangente de l’angle :
![]()
Signification de la pente d’une droite
Avec toutes les informations ci-dessus, nous savons déjà parfaitement comment trouver la pente d’une droite. Mais vraiment… que signifie la pente d’une droite ?
La pente d’une ligne indique les unités verticales que la ligne monte pour chaque unité horizontale du graphique.
Par exemple, dans la représentation de la ligne suivante, vous pouvez voir qu’elle avance de 2 unités verticales pour chaque unité horizontale, car sa pente est égale à 2.

De plus, la pente d’une droite indique aussi sa raideur :
- Si une droite est croissante (montante), sa pente est positive.
- Si une droite est décroissante (descendante), sa pente est négative.
- Si une droite est complètement horizontale, sa pente est égale à 0.
- Si une droite est complètement verticale, sa pente est égale à l’infini.


Position relative des lignes
D’autre part, la position relative entre deux lignes peut également être connue à partir des propriétés des pentes :
- Si deux droites ont des pentes différentes, cela signifie qu’elles se croisent , c’est-à-dire qu’elles se croisent en un point.
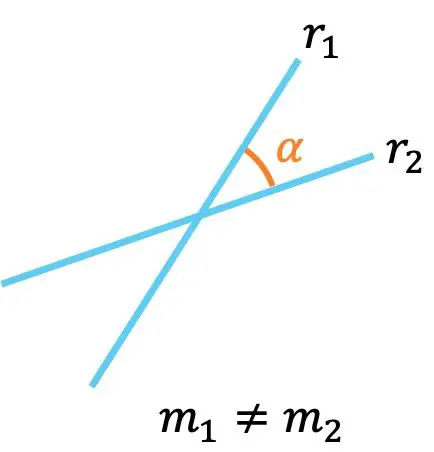
De plus, l’angle entre les deux lignes à travers leurs pentes peut être calculé avec la formule suivante :
![]()
- Deuxièmement, si deux droites ont la même pente, cela implique qu’elles sont parallèles .

- Enfin, les pentes de deux droites perpendiculaires ou orthogonales (qui forment 90º) remplissent la condition suivante :

C’est un moyen de savoir si deux lignes sont parallèles ou perpendiculaires l’une à l’autre, cependant, il existe d’autres méthodes et certaines sont encore plus rapides. Pour en savoir plus vous pouvez aller à l’explication de la perpendicularité et du parallélisme entre les droites . De plus, ces pages expliquent également comment trouver une droite perpendiculaire (ou parallèle) à une autre.
Problèmes résolus de la pente d’une droite
Exercice 1
Trouvez la pente de la droite qui passe par les deux points suivants :
![]()
Pour calculer la pente de la droite, il faut utiliser la formule :
![]()
Exercice 2
Calculez la pente de la droite qui passe par les deux points suivants :
![]()
Pour trouver la pente de la droite, il faut utiliser la formule :
![]()
Exercice 3
Quelle est la pente de chaque droite ?
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d405c8176957af59906c98149714570_l3.png)
A) La droite est exprimée sous la forme d’une équation implicite, donc sa pente est de 2 (le terme qui accompagne la
![]() ).
).
B) La droite est définie par son équation point-pente, donc sa pente est 4 (le nombre avant les parenthèses).
C) La droite est sous forme d’équation implicite, donc sa pente est :
![]()
D) La ligne est définie sous la forme d’équations paramétriques, de sorte que nous devons d’abord trouver son vecteur directeur et avec lui nous pouvons calculer la pente de la ligne. Ainsi, les composantes du vecteur directeur sont les termes qui accompagnent le coefficient
![]()
![]()
Et une fois que nous connaissons le vecteur directeur de la droite, nous pouvons déterminer la pente de la droite :
![]()
Exercice 4
Déterminez la pente de chaque droite représentée graphiquement :

bleu droit
La ligne bleue augmente d’un Y pour chaque X, donc sa pente est égale à 1.
![]()
vert droit
La ligne verte augmente de trois Y pour chaque X, donc sa pente est de 3 .
![]()
ligne rouge
La ligne rouge diminue de deux Y pour chaque X, donc sa pente est égale à -2 .
![]()