La notation mathématique est un moyen de communiquer des idées et des calculs grâce à l’utilisation de symboles. Bien qu’à première vue, cela puisse sembler déroutant, avec un peu de pratique, vous pourrez l’interpréter facilement. Dans cet article, nous allons vous montrer la signification de tous les symboles utilisés dans cette notation et quelques exemples sur la façon de les appliquer.
Qu’est-ce que la notation mathématique ?
La notation mathématique est une façon d’écrire les valeurs et les expressions utilisées en mathématiques. Cette technique permet aux mathématiciens d’énoncer des idées de manière concise et précise . La notation mathématique permet également à ceux qui pratiquent ou étudient les mathématiques de mieux comprendre les concepts.
Il ne faut pas confondre le langage des mathématiques avec la notation scientifique, qui est une façon d’écrire des valeurs numériques. Alors que la notation mathématique est plutôt un ensemble de symboles qui permettent d’écrire des expressions complexes, tout comme un langage. Nous reviendrons plus en détail sur ce sujet plus tard.
Comment lire la notation mathématique ?
Apprendre à interpréter la notation mathématique est plus facile qu’il n’y paraît, il vous suffit d’apprendre la signification de chaque symbole et une fois que vous l’aurez fait, vous pourrez lire tout ce qui est écrit en notation mathématique. C’est aussi simple que cela, même si cela nécessite évidemment de la pratique et beaucoup de temps d’étude.
Les expressions mathématiques sont très logiques et suivent toujours des modèles, par conséquent, il vous suffit de mémoriser les règles et vous saurez ensuite les extrapoler à n’importe quelle situation. On pourra même décrire des calculs très complexes, c’est la magie du langage mathématique, qui permet de communiquer des messages très élaborés de manière méthodique.
Composants de la notation mathématique
La notation mathématique est composée d’une série de symboles qui représentent des nombres, des opérations et les relations entre eux. Ces symboles peuvent sembler compliqués au début, mais avec un peu de pratique et de compréhension, l’interprétation de la notation mathématique devrait devenir un jeu d’enfant.
Ensuite, nous expliquerons en détail les quatre types d’éléments que l’on peut trouver dans le langage mathématique. En commençant par le plus basique et en terminant par le plus complexe et le plus abstrait. Et une fois l’explication théorique terminée, nous parlerons des types de notations numériques qui existent.
Nombres et ensembles de nombres
Dans un premier temps, il faut définir les nombres mathématiques , c’est un concept mathématique qui désigne une quantité en rapport avec une unité. Nous pouvons décrire n’importe quelle valeur numérique, en suivant le système de numérotation décimale et en combinant les symboles suivants : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
Si nous ordonnons les nombres selon différentes propriétés, nous obtenons plusieurs catégories de nombres, appelées ensembles de nombres. Et ces groupes de valeurs ont aussi leurs propres symboles qui les désignent, dans la liste suivante nous les présentons tous avec le nom du groupe correspondant :
- ℙ : nombres premiers
- ℕ : nombres naturels
- ℤ : Entiers
- ℚ : nombres rationnels
- ℝ : Nombres réels
- 𝕀 : nombres imaginaires
- ℂ : nombres complexes
- ℍ : Quaternions
Ces symboles sont généralement utilisés dans nos calculs, pour déterminer une large gamme de nombres, en une seule fois. Par exemple, si nous avons une expression qui accepte de nombreuses valeurs en conséquence, au lieu d’écrire les nombres un par un, il nous sera plus facile de spécifier ces valeurs à travers le symbole correspondant à leur groupe numérique .
Opérateurs et quantificateurs
Maintenant que nous avons discuté des nombres, qui sont l’essence des mathématiques, nous devons parler des opérateurs et des quantificateurs . Les premiers sont tous ces symboles qui nous permettent de représenter une opération : addition (+), soustraction (-), multiplication (x ou ·), division (÷), entre autres.
Cependant, nous avons également deux autres types d’opérateurs, qui sont les opérateurs logiques et les opérateurs relationnels. Le premier exprime la conjonction, la disjonction et la négation. Ils nous aident à proposer des opérations logiques , qui, contrairement aux opérations arithmétiques, ne fonctionnent pas avec des nombres, mais avec des propositions mathématiques.
Tandis que la seconde, nous permet d’établir des équivalences et des relations entre des valeurs ou des expressions mathématiques. Ces symboles peuvent être utilisés dans les calculs arithmétiques (pour ordonner des nombres), mais ils sont plus importants en algèbre, lorsque nous avons des variables (plus à ce sujet dans deux sections).
Dans la liste suivante, vous pouvez trouver la définition de tous les opérateurs dont nous avons discuté jusqu’à présent :
| Symbole | Définition | Type |
| + | Ajout | opérateur arithmétique |
| – | Soustraction | opérateur arithmétique |
| X, *, · | Multiplication | opérateur arithmétique |
| ÷ | Division | opérateur arithmétique |
| x² | autonomisation | opérateur arithmétique |
| √ | dépôt | opérateur arithmétique |
| ET | Conjonction | opérateur logique |
| SOIT | Disjonction | opérateur logique |
| NON | Le déni | opérateur logique |
| = | Égal à | opérateur de relation |
| > | Plus grand que | opérateur de relation |
| < | Plus petit que | opérateur de relation |
| >= | Meilleur que ou égal | opérateur de relation |
| <= | inférieur ou égal à | opérateur de relation |
| ≠ | n’est pas égal à | opérateur de relation |
| ≡ | Exactement le même | opérateur de relation |
| ≈ | à peu prés égal | opérateur de relation |
| ≃ | Équivalent à | opérateur de relation |
| ∝ | Proportionnel | opérateur de relation |
Bien qu’il existe également cinq autres opérateurs logiques, qui sont utilisés pour expliquer la logique mathématique à partir de la théorie des ensembles. Qui est une branche qui applique la logique des ensembles , qui est utilisée dans le calcul, la géométrie, les statistiques… Ensuite, nous vous montrons les symboles qui sont utilisés et leur définition.
| Symbole | Définition |
| x ∈ A | x appartient à A |
| x ∉ A | x n’appartient pas à A |
| ∪ | syndicat |
| ∩ | Intersection |
| ⊂ | Inclusion |
Quant aux quantificateurs, nous pouvons les définir comme des symboles qui indiquent le nombre d’éléments d’un ensemble remplissant une certaine condition (équivalence, ordre, appartenance, etc.). Il existe une grande variété d’opérateurs, mais parmi les plus utilisés, on peut souligner :
| Symbole | Définition | Type |
| ∀x | pour tout x | quantificateur |
| ∃x | Il y a au moins un x | quantificateur |
| ∄x | il n’y a pas de x | quantificateur |
| ∃!x | Il n’y a qu’un seul x | quantificateur |
| | | Tel que | quantificateur |
| ∴ | Donc | quantificateur |
Les expressions mathématiques et leurs relations
Avec les symboles que nous avons couverts jusqu’à présent, vous pouvez comprendre beaucoup de mathématiques, mais nous n’avons pas encore expliqué leurs applications ou leurs relations dans des expressions complexes, comme les opérations combinées ou le calcul algébrique. De plus, il y a encore des symboles de relation à discuter. Ce sont ceux que nous allons voir dans cette section.
En commençant par les symboles de regroupement, ce sont les parenthèses, les crochets et les accolades. Ces éléments sont essentiels dans la désignation de formules complexes. Sa fonction principale est de donner la priorité à certains calculs, au sein d’une expression globale. Et il existe différents niveaux de priorité parmi les trois types. Dans cette expression, vous pouvez voir l’ordre d’écriture 3 {[2 + (3 – 2) · 2] – 4}.
| symboles | Définition | Priorité |
| “(” et “)” | Parenthèse | Priorité maximale |
| “[” et “]” | Supports | deuxième priorité |
| “{” et “}” | Clés | troisième priorité |
Et pour terminer cette catégorie, nous parlerons des sommations (Σ) et des produits (∏) , qui sont des éléments qui permettent de décrire des additions et des multiplications répétées. La sommation équivaut à dire : « somme de Xi, où i prend les valeurs de 1 à an ». Et le produit est le même, mais au lieu d’additionner, on multiplie.
analyse algébrique
La première chose à discuter à propos des symboles algébriques est les variables, qui sont représentées par les lettres de l’alphabet. Leur fonction est d’ imiter un nombre , mais elles n’ont pas de valeur fixe commeles constantes mathématiques , elles peuvent donc prendre de nouvelles valeurs. Ceci s’applique aux équations, limites, dérivées, intégrales, matrices…
Enfin, nous voulons parler des représentations de toutes ces opérations algébriques dont nous venons de parler dans ce dernier paragraphe. Depuis, ils sont la base de l’algèbre et vous devez savoir quelle est leur symbologie. Ensuite, nous vous montrons un tableau avec ses différents symboles et une brève définition :
| Symbole | Définition |
| lim x → b | Limite (lorsque x tend vers b) |
| y’, ƒ’ (x), dy / dx | dérivé |
| ∫ | Complet |
| À mxn | Matrice des dimensions mxn |
Conclusion sur les symboles du langage mathématique
Jusqu’à présent, vous avez vu tous les symboles importants qui sont traités en mathématiques, il y en a évidemment encore à discuter. Mais, celles-ci sont plus spécifiques à chaque sous-catégorie des mathématiques : géométrie, statistique, algèbre… Nous allons donc clore ce sujet et parler des notations numériques.
Types de notations numériques
Dans cette section, nous allons voir toutes les manières d’exprimer les nombres mathématiques, car il existe différentes notations pour le faire. Au début, nous avons évoqué plus haut le système de numération décimale, qui est le plus utilisé par les mathématiciens. Ensuite, nous l’expliquerons plus en détail et vous montrerons d’autres types de notation mathématique :
notation décimale
Le système numérique décimal est un système numérique positionnel (système dans lequel la position de chaque chiffre déterminera sa valeur) est basé sur les multiples et sous-multiples du nombre 10. Puisque dix est le nombre utilisé comme base numérique . Par conséquent, les dix symboles numériques que nous utiliserons sont les suivants : 1, 2, 3, 4, 5, 6, 7, 8, 9 et 0.
La valeur de ces nombres est déterminée à partir de la somme des chiffres multipliée par les puissances en base dix, établies en fonction de la position . Et il est très important que vous vous souveniez que pour écrire un nombre inférieur à un, il faut utiliser la virgule décimale. Vous trouverez ci-dessous un exemple :
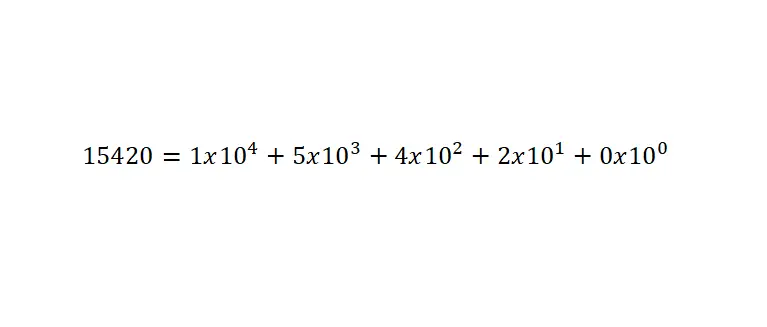
Notation scientifique
La notation sous forme exponentielle ou notation scientifique est clairement l’un des types d’écriture les plus utilisés dans le domaine de la science et de la technologie. En effet, cela nous permet d’exprimer de manière simple des nombres très grands et très petits. Pour comprendre la définition de la notation scientifique, nous allons expliquer comment passer un entier à cette notation :
- Déplacer la virgule : il faut déplacer la virgule autant de fois que nécessaire jusqu’à atteindre le premier chiffre (vers la gauche si on a un très grand nombre et vers la droite si on a un très petit nombre).
- Établissez la base : écrivez ce dernier chiffre multiplié par dix, donc, à côté de la valeur que vous avez obtenue en déplaçant la virgule d’un côté, vous devez écrire une multiplication par dix : « x 10 ».
- Ajoutez un exposant : avec une valeur égale au nombre de fois où vous avez déplacé la virgule décimale. Avec de grands nombres, vous laisserez l’exposant en positif, mais, en petits nombres, vous devez l’écrire avec un signe négatif.
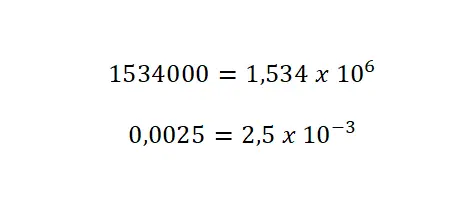
notation hexadécimale
Le système hexadécimal est basé sur 16, ce qui signifie qu’il utilise seize symboles différents : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E et F. Comme vous pouvez le voir, ce système de numérotation est composé des chiffres du système décimal et de six lettres. Cette notation est généralement utilisée notamment en informatique et tout ce qui touche à l’informatique.
Il est important de préciser que puisqu’il a des symboles en commun avec d’autres types de notation, nous devons toujours indiquer qu’il est écrit en hexadécimal au moyen d’ une parenthèse et de l’indice 16 . Dans l’exemple suivant, vous pouvez voir à partir d’un exemple très clair la conversion d’un nombre hexadécimal en notation décimale :
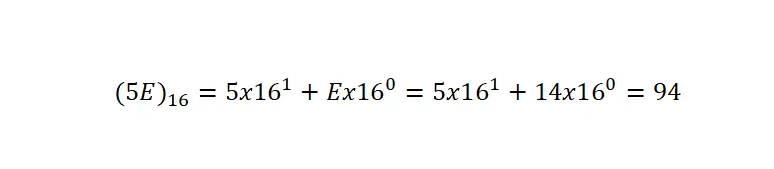
Pour convertir un nombre hexadécimal en une expression décimale, nous devons décomposer le nombre en ses multiplications de base, comme nous l’avons fait dans la notation décimale, mais en changeant la base en 16 . Ensuite, nous multiplierons chaque chiffre par seize élevé à la position que ce chiffre spécifique occupe moins un.
notation octale
Le dernier système dont nous parlerons est la notation octale , qui a une base de 8. Cela signifie qu’elle n’utilise que huit symboles ou chiffres : 0, 1, 2, 3, 4, 5, 6 et 7. C’est le système de numérotation le moins utilisé de tous ceux que nous avons expliqués. Il est à noter que les conversions de cette notation se font selon la même procédure que les précédentes.
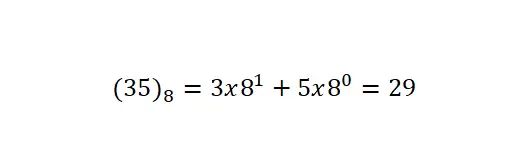
notation romaine
Enfin, nous pouvons parler du système de chiffres romains , qui n’est pas très utilisé aujourd’hui, mais dans le passé, il était très important dans le domaine des mathématiques. Puisque c’était l’une des notations qui ont donné vie aux mathématiques.
Votre écriture est limitée à 7 symboles : I (1), V (5), X (10), L (50), C (100), D (500) et M (1000). Et en combinant ces lettres, tous les chiffres sont écrits. Si vous voulez savoir comment ils se combinent pour donner naissance à d’autres nombres plus grands, nous vous recommandons de lire notre article à leur sujet, en accédant via le dernier lien.
Comment améliorer les performances de lecture en notation mathématique ?
Il existe plusieurs façons d’ améliorer les performances de lecture de la notation mathématique. Une façon consiste à lire les symboles et les chiffres à haute voix. Une autre façon est de vous familiariser avec les symboles et leur signification. Vous pouvez également vous entraîner à lire la notation mathématique à l’aide d’exercices et de problèmes.
Nous espérons que nous vous avons aidé avec ce guide, s’il vous plaît, si vous avez des questions, n’hésitez pas à les écrire dans les commentaires . Ou si vous souhaitez apporter une contribution sur le sujet, nous espérons également le voir dans les commentaires. Cela dit, nous vous laissons un article sur comment apprendre les mathématiques , au cas où vous voudriez continuer à lire.