Vous avez sûrement entendu parler de l’ ensemble des nombres imaginaires ou de l’unité imaginaire. C’est un concept mathématique qui découle du besoin mathématique d’exprimer des nombres qui n’appartiennent pas aux nombres réels .
Que sont les nombres imaginaires ?
Les nombres imaginaires sont ceux qui, mis au carré, donnent un nombre négatif . Par conséquent, ce sont des valeurs équivalentes à la racine carrée d’un nombre négatif. Par exemple, l’unité imaginaire (le nombre i) est égale à la racine carrée de -1.
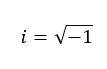
Ces nombres n’appartiennent pas aux nombres réels, car dans l’ensemble réel, les racines négatives ne peuvent pas être résolues. C’est là que réside l’importance du décor imaginaire. Cet ensemble a été inventé pour pouvoir traiter les racines négatives et pour pouvoir résoudre toutes ces équations et problèmes quadratiques qui “n’ont pas de solution”, car ils nous donnent une racine négative.
Pour éviter toute confusion, il est important de faire la distinction entre les nombres imaginaires et les nombres complexes . Les complexes sont des nombres composés d’ un nombre réel et d’un nombre imaginaire . Par conséquent, les imaginaires sont une sous-catégorie de complexes, qui n’ont pas de partie réelle. Dans le tableau suivant, vous pourrez mieux apprécier les différences.
| nombre complexe | partie royale | partie imaginaire | Description |
| 4+7i | 4 | 7i | Complexe |
| 3 | 3 | 0 | pur royal |
| 2i | 0 | 2i | Pur Imaginaire |
Pour finir de situer cet ensemble numérique, nous pouvons visualiser dans l’image suivante une structure de tous les ensembles. Comme nous pouvons le voir, les nombres complexes englobent tous les types de nombres , ceux-ci à leur tour peuvent être divisés en nombres réels et en nombres imaginaires purs (qui sont ceux dont nous traitons dans cet article).

Exemples de nombres imaginaires
A partir de l’unité imaginaire (i), on peut déduire d’autres nombres imaginaires. Il vous suffit d’appliquer la formule suivante :
m = r je
Où m est un nombre imaginaire, r est un nombre réel et i est l’unité imaginaire. Dans l’image suivante, vous pouvez voir comment nous obtenons différents imaginaires à partir de racines négatives.
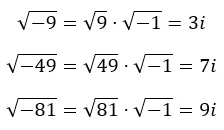
En fait, on peut l’extrapoler à l’expression suivante :
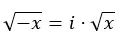
Propriétés des nombres imaginaires
Les nombres imaginaires ont un certain nombre de propriétés très intéressantes . Certains dont nous avons déjà parlé au début de cet article et d’autres non :
- Les imaginaires n’appartiennent pas à l’ensemble des réels, car ce sont des nombres qui physiquement n’existent pas et ne peuvent pas être représentés dans notre réalité.
- Ce sont des valeurs équivalentes aux racines négatives.
- Ils peuvent être représentés graphiquement sur la ligne imaginaire.
- Les puissances imaginaires (c’est un concept que nous expliquerons dans la section suivante) sont d’une grande aide pour simplifier les calculs numériques impliquant des valeurs imaginaires.
- La formule d’Euler est une expression qui permet de relier des nombres imaginaires à des nombres réels.
Opérations avec des nombres imaginaires
Maintenant que vous connaissez toutes les caractéristiques importantes des nombres imaginaires, il est temps d’apprendre à résoudre des opérations avec eux. Pour opérer avec des valeurs imaginaires , vous devez suivre les mêmes étapes que vous suivez pour opérer avec des valeurs réelles, sauf que vous devez prendre en compte un concept : les puissances imaginaires.
pouvoirs imaginaires
Les nombres imaginaires ont une propriété très intéressante qui se produit lorsque vous multipliez l’unité imaginaire par elle-même. Autrement dit, cela se produit lorsque vous faites des puissances de l’unité imaginaire . Si nous écrivons les puissances, comme dans la liste suivante, un modèle peut être découvert :
je 0 = 1
je 1 = je
je 2 = je · je = ( √ -1) · ( √ -1) = -1
je 3 = je 2 je = (-1) je = -je
je 4 = je 2 je 2 = (-1) (-1) = 1
Connaître ce concept nous facilitera grandement la résolution d’opérations avec des nombres imaginaires, car nous pourrons simplifier les opérations difficiles et les rendre un peu plus faciles. De plus, la bonne chose à propos de ces pouvoirs est qu’ils se répètent indéfiniment. Nous pouvons le voir, si nous ajoutons quelques pouvoirs supplémentaires :
je 5 = je
je 6 = -1
je 7 = -je
je 8 = 1
etc.
Et avec les puissances négatives, cela arrive aussi.
Opérations arithmétiques avec des nombres imaginaires
Ensuite, nous allons vous donner un exemple de chaque opération arithmétique de base, afin que vous puissiez voir les calculs de nombres imaginaires résolus.
- Addition de nombres imaginaires : c’est exactement la même chose que l’addition de nombres réels, il suffit de ne pas oublier d’ajouter le i.
4i + 3i = 7i
- Soustraction de nombres imaginaires : les soustractions sont également résolues de la même manière que dans l’ensemble réel.
4i – 3i = je
- Multiplication de nombres imaginaires : dans ce cas, il faut garder à l’esprit les puissances imaginaires que nous avons évoquées précédemment.
3i 4i = 12 je 2 = 12 (-1) = -12
- Division de nombres imaginaires : dans ce type de division, nous devons également être vigilants, au cas où nous rencontrions une puissance imaginaire, ce qui nous permet de simplifier l’opération.
12i ÷ 4i = 3
Équations avec des nombres imaginaires
Comme nous l’avons déjà dit, lorsque nous résolvons des équations dans l’ensemble réel, il arrive parfois que nous obtenions des racines négatives et, par conséquent, les équations “n’ont pas de solution” . Mais, maintenant que nous connaissons les imaginaires, nous pouvons résoudre ces équations. Voyons un exemple :
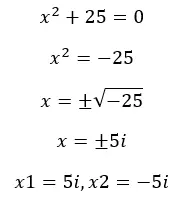
A quoi servent les nombres imaginaires ?
Les nombres imaginaires naissent de la nécessité de pouvoir exprimer des valeurs qui sont en dehors de l’ensemble réel. C’est pourquoi, au début, il peut sembler qu’ils n’ont pas beaucoup d’applications utiles . Mais la vérité est que c’est tout le contraire. Parce que, lorsque nous les combinons avec les vrais, nous obtenons les nombres complexes.
Et ceux-ci ont de nombreuses applications. Ils sont utilisés pour étudier le courant alternatif (car il a des valeurs négatives), son utilisation est également très répandue dans le domaine des ondes (qui a des applications en physique, en électronique des télécommunications et en mécanique quantique). Parmi de nombreuses autres utilisations.
De plus, il arrive souvent que lorsque vous résolvez une équation quadratique , la valeur vous donne une racine négative et vous ne pouvez pas opérer… Avec les imaginaires , vous pouvez les résoudre . Donc, en guise de conclusion, on peut dire que c’est un ensemble qui nous permet d’élargir nos connaissances plus abstraites.