Vous avez sûrement entendu parler des nombres complexes . Ils sont peut-être l’ensemble de nombres le plus difficile à gérer, car ils combinent des nombres réels et imaginaires. Son unification permet d’étudier des comportements numériques qui ne peuvent être traités à partir de l’ensemble des nombres réels.
Que sont les nombres complexes ?
Les nombres complexes sont la combinaison d’un nombre réel et d’un nombre imaginaire . Par exemple, 4 + 5i est un nombre complexe qui a une partie réelle égale à 4 et une partie imaginaire égale à 5i. En général, nous pouvons les exprimer par la formule suivante :
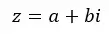
Où, Re(z) = a et Im(z) = b
Comme nous l’avons bien dit, les complexes sont le plus grand ensemble ou ensemble global , qui comprend à la fois des nombres réels et des nombres imaginaires. Ensuite, nous vous montrons un petit schéma de la structure hiérarchique de tous les ensembles :

Par conséquent, lorsque nous avons une combinaison d’un nombre réel et d’un nombre imaginaire, nous avons un nombre complexe. Mais, il y a des moments où l’une des deux parties est égale à zéro. Que se passe-t-il dans ces cas ? Eh bien, nous avons toujours affaire à des complexes, car l’ensemble complexe englobe tous les autres ensembles numériques. Mais, nous entrons dans une sous-catégorie différente :
| nombre complexe | partie royale | partie imaginaire | Sous-catégorie |
| 2+5i | 2 | 5i | Complexe |
| 4 | 4 | 0 | pur royal |
| 3i | 0 | 3i | Pur Imaginaire |
Lorsqu’on a un réel pur, comme la valeur imaginaire b est égale à zéro, le nombre complexe qui reste est équivalent à :
z = une + 0i = une
Par contre, lorsqu’on a un imaginaire pur, a est égal à zéro et, par conséquent, le nombre complexe reste le suivant :
z = 0 + bi = bi
Représentation graphique des nombres complexes
Pour représenter les nombres complexes, on utilise le plan complexe . Qui est formé de deux lignes : la ligne réelle et la ligne imaginaire. Ces deux droites numériques servent à localiser graphiquement les nombres de chaque ensemble et si on les met ensemble, on obtient un plan, tel que :

L’axe X est appelé axe réel car c’est là que se trouvent les valeurs de la partie réelle. Alors que l’axe Y est appelé l’axe imaginaire, c’est là que les valeurs imaginaires sont écrites. Voyons un exemple, nous placerons le nombre 3 + 2i dans le plan complexe.

Comme vous l’avez vu sur l’image, nous avons localisé le nombre en utilisant les nombres 3 et 2 comme coordonnées, chacun pour un axe. Si vous souhaitez en savoir plus sur la représentation des nombres complexes, nous vous recommandons de lire cet article.
Quels sont les types de nombres complexes ?
Maintenant, nous allons voir les manières dont nous disposons pour exprimer un nombre complexe. Jusqu’à présent, nous n’avons vu que la forme de base (dite forme binomiale), qui s’écrit comme une somme : partie réelle plus partie imaginaire.
Mais, en réalité, nous avons trois formes : le binôme, le polaire et le trigonométrique . Chaque type d’expression a ses propriétés et est utilisé dans une situation ou une autre. Nous allons donc tous les expliquer et montrer comment passer de l’un à l’autre.
1. Forme binomiale
Les nombres complexes sous forme binomiale s’écrivent comme la somme de la partie réelle et de la partie imaginaire : a + bi. Par exemple, le nombre 6 + i est un complexe exprimé en notation binomiale. Dans celui-ci, la formule est toujours la même :

Par conséquent, pour exprimer un nombre complexe sous forme binomiale, il suffit de connaître sa valeur réelle et sa valeur imaginaire.
Par exemple, la valeur 3 + 2i est sous forme binomiale et, comme nous l’avons vu précédemment, elle est représentée comme suit :

La forme binomiale est principalement utilisée pour résoudre l’addition et la soustraction de nombres complexes.
2. Forme polaire
Pour exprimer les nombres complexes sous forme polaire , il faut calculer leur module |z| et son argumentation. La forme polaire est principalement utilisée lorsque nous devons résoudre la multiplication et la division de nombres complexes.
Pour calculer le module du nombre complexe, il suffit de faire le module de a et b, comme expliqué dans la formule suivante :

Et pour calculer l’argument ou l’angle de z, nous devons calculer l’arc tangente de b entre a :

Il est important de noter que pour déterminer exactement la valeur de l’angle α, il est nécessaire de repérer dans quel quadrant il se situe. En effet, la fonction arctangente ne calcule que les angles compris entre π/2 et -π/2. Pour préciser dans quel quadrant se situe le nombre complexe, il faut regarder les valeurs a et b (si elles sont positives ou négatives) :
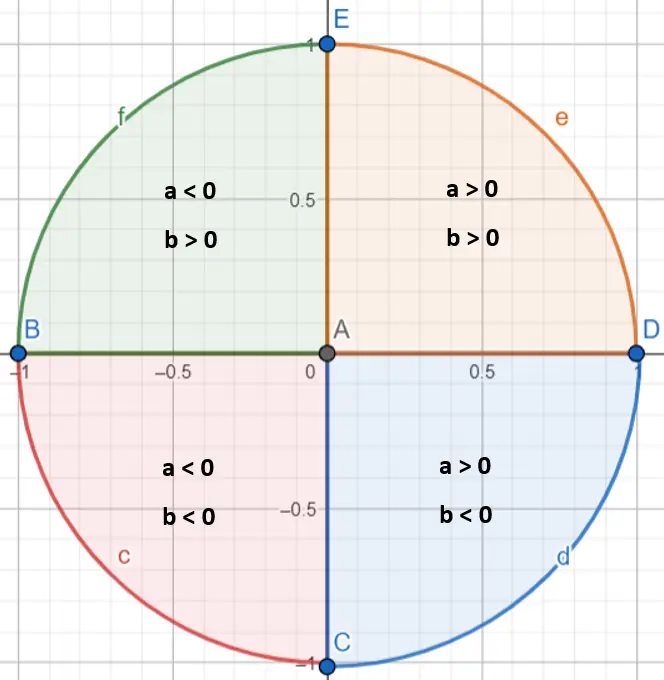
Une fois que nous savons dans quel quadrant se situe notre numéro, nous devons suivre quelques règles :
- Si le nombre complexe est dans le premier quadrant (a > 0 et b > 0), nous laisserons l’argument tel quel.
- Si le nombre complexe est dans le deuxième quadrant (a < 0 et b > 0), nous ajouterons π à l’argument.
- Si le nombre complexe est dans le troisième quadrant (a < 0 et b < 0), nous soustrairons π de l’argument.
- Si le nombre complexe est dans le quatrième quadrant (a > 0 et b < 0), nous ajouterons 2π à l’argument.
Dans le cas où vous ne savez pas de quoi on parle quand on dit quadrant, on vous conseille de consulter notre article sur les rapports trigonométriques .
Une fois que nous connaissons la grandeur et l’argument de z, nous pouvons exprimer le nombre complexe sous forme polaire. Bien que, ce formulaire accepte plusieurs nomenclatures, les deux principales sont :

Par exemple, si nous voulons passer le nombre 3 + 5i à polaire, nous devons simplement suivre la procédure suivante.
On calcule d’abord le module :
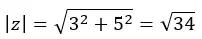
Ensuite, nous calculons l’argument, qui est dans le premier quadrant, donc il reste tel que nous l’avons calculé.
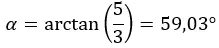
Et on exprime le nombre sous forme polaire :
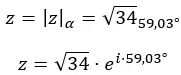
Sa représentation graphique est la suivante :
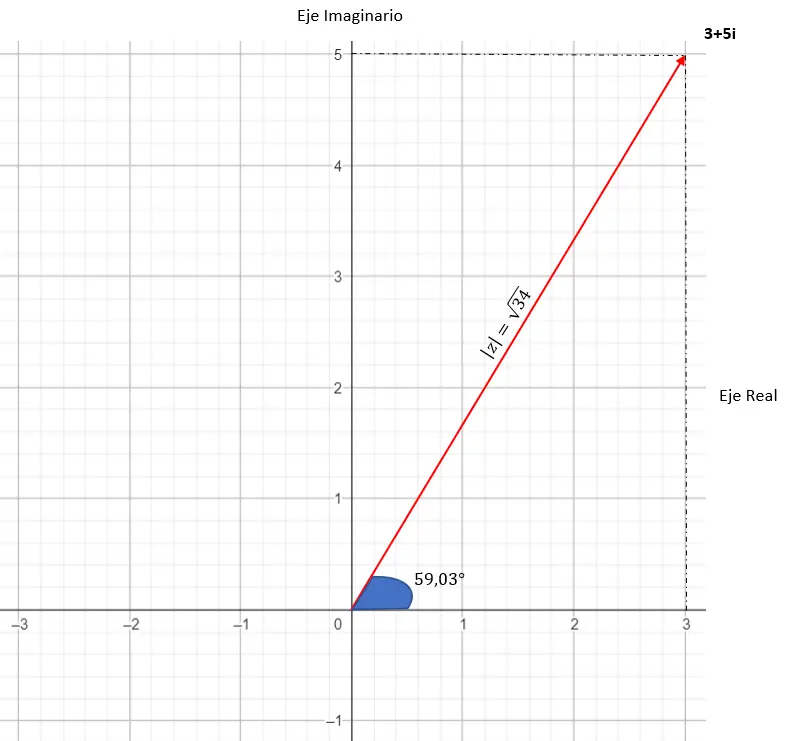
3. Forme trigonométrique
Enfin, nous avons la notation trigonométrique , qui est calculée à partir de la formule d’Euler :

Par exemple, pour exprimer le nombre 4 – 3i sous forme trigonométrique, nous suivons la procédure suivante :
Nous commençons par calculer le module et l’argument avec les formules que nous avons utilisées dans la section sur la forme polaire.
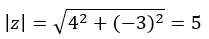
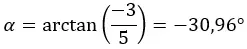
ATTENTION : L’argument est dans le quatrième quadrant, car (a > 0 et b < 0).
Nous ajoutons les données dans l’équation sous forme trigonométrique.
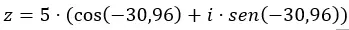
Et nous avons déjà le nombre exprimé sous forme trigonométrique. Sa représentation graphique est la suivante.
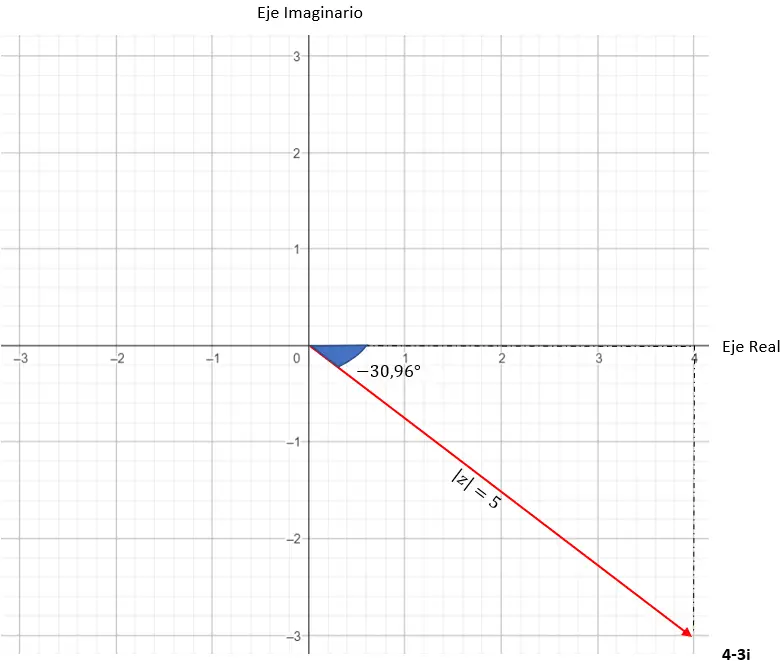
Comment passer d’un type à l’autre ?
Vous connaissez maintenant toutes les façons d’exprimer un nombre complexe. Et tout au long de la dernière section, vous avez pu voir comment accéder à chacun d’eux, mais avant de terminer, nous voulons faire un bref résumé de la façon de passer d’un formulaire à l’autre. Seulement, vous devez utiliser les formules que nous avons vues dans la section précédente.
Du binôme à la forme polaire et inversement
Pour passer du binôme au polaire, nous proposons le schéma suivant :
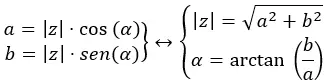
Nous avons vu un exemple plus tôt où nous sommes passés du binôme au polaire, alors maintenant nous allons passer du polaire au binôme en utilisant le schéma ci-dessus. Nous devons convertir √41 38,66 en binôme.
On calcule d’abord le a.
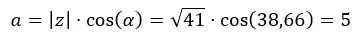
Ensuite, nous calculons b.
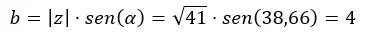
Et nous l’exprimons sous forme binomiale.
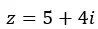
La représentation graphique de ce nombre ressemble à ceci :
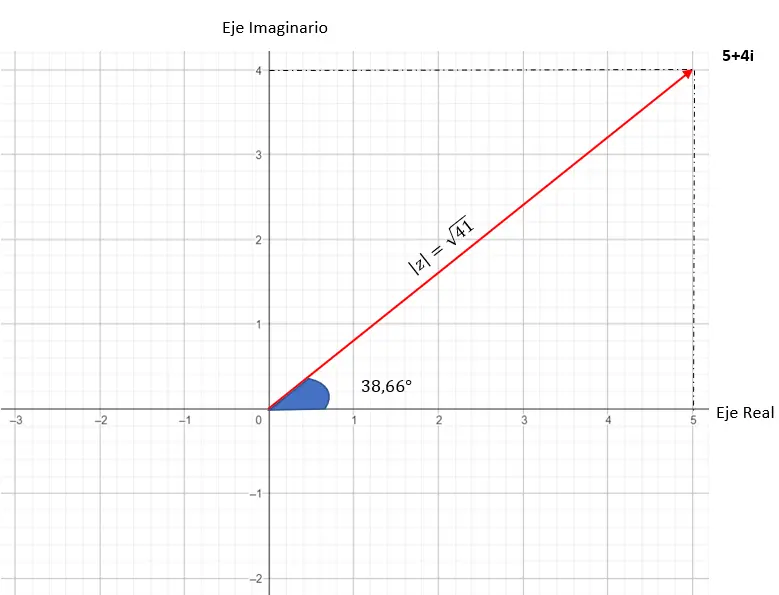
De la forme binomiale à la forme trigonométrique et inversement
Pour passer du binôme au trigonométrique, il faut aussi appliquer les formules dont nous avons parlé dans la section précédente. De cette façon, nous calculons d’abord le module et l’argument, puis nous mettons ces données dans l’équation de la forme trigonométrique. Pour donner un exemple, nous allons passer le nombre z = 3 + 2i au trigonométrique.
Nous calculons d’abord le module et l’argument.
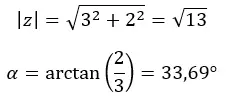
ATTENTION : L’argument est dans le premier quadrant, car (a > 0 et b > 0).
Ensuite, on complète l’équation de forme trigonométrique avec ces données.
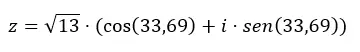
Et si on veut passer du trigonométrique au binomial, il suffit de résoudre l’expression précédente.
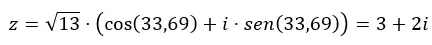
De la forme polaire à la forme trigonométrique et inversement
Enfin, nous allons passer de la forme polaire à la forme trigonométrique. Ce qui est assez simple, car ces deux formes sont exprimées par les deux mêmes valeurs : modulo et argument . Il vous suffit donc de remplir les formules et c’est tout.
Donnons un exemple, nous allons convertir le nombre z = √85 12,53 en forme trigonométrique.
On reformule les deux variables (module et argument) dans l’équation de la forme trigonométrique :
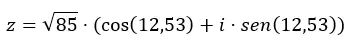
Alors maintenant que vous savez comment passer d’une forme à l’autre, nous vous recommandons de pratiquer un peu avec quelques exercices . De cette façon, vous consoliderez les connaissances apprises dans cet article. Si vous avez des questions concernant ce sujet, n’hésitez pas à les laisser dans les commentaires. Et si vous voulez en savoir plus sur les nombres complexes, consultez les liens ci-dessous.