Zwaartekracht is een natuurlijk fenomeen dat een aantrekkingskracht genereert tussen twee of meer fysieke lichamen met massa. Dit verklaart de versnelling die een object ervaart wanneer het zich dicht bij een ander bevindt. De zwaartekracht of de aantrekkingskracht van de zwaartekracht kan worden berekend op basis van de massa van twee of meer objecten en de afstand daartussen. Vervolgens leggen we uit hoe dit wordt berekend en wat de effecten ervan zijn.
zwaartekracht rekenmachine
Met het volgende hulpmiddel kun je de zwaartekracht tussen twee lichamen berekenen. De werking ervan is heel eenvoudig, je hoeft alleen maar de waarden van de twee massa’s in te voeren en de afstand waarop ze zich bevinden. Dan hoeft u alleen maar op de knop “Bereken” te drukken en u krijgt onmiddellijk een zeer nauwkeurig resultaat .
De wet van universele zwaartekracht
Deze wet stelt de aantrekkingskracht vast tussen twee of meer lichamen die massa hebben. Wat deze wet ons dus vertelt (afgezien van de beroemde formule van universele zwaartekracht) is dat hoe groter de lichamen en hoe dichter ze bij elkaar zijn, hoe groter de aantrekkingskracht is.
Als we dit concept daarom toepassen op de astrofysica, zal de zwaartekracht ook groter zijn, aangezien de studieobjecten (astronomische lichamen) groter zijn. Deze proportionele relatie geeft ons een klein idee van hoe de zwaartekracht werkt, maar als je wilt leren hoe je de exacte waarde van de zwaartekracht kunt berekenen, raden we je aan verder te lezen.
zwaartekracht formule
Om de aantrekkingskracht tussen twee objecten te berekenen, passen we de volgende formule toe:
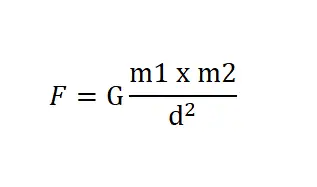
Bij de uitdrukking zijn de volgende variabelen betrokken: massa van het eerste object (m1), massa van het tweede object (m2), afstand (d) en zwaartekrachtconstante (G) = 6,6742 · 10 -11 . Als je al deze waarden kent, kun je de aantrekkingskracht berekenen die de zwaartekracht tussen twee objecten genereert. Merk op dat de massa’s moeten worden uitgedrukt in kilogram, de afstand in meters en dat het resultaat wordt verkregen in Newton, de eenheid die overeenkomt met kracht.
de newton
De Newton (N) is de eenheid voor het meten van kracht in het SI (International System of Units), genoemd naar de natuurkundige Isaac Newton. De definitie ervan is de kracht die gedurende één seconde wordt uitgeoefend op een massa van één kilogram, zodat deze beweegt met een snelheid van 1 m/s, vergeleken met de vorige snelheid. Met andere woorden: 1 Newton = 1 kg x (m/s) 2 . Deze definitie is gebaseerd op de tweede wet of het fundamentele principe van Newton .
afgeleide formules
Uit de universele zwaartekrachtformule kunnen we de verschillende variabelen isoleren, afhankelijk van wat we willen berekenen. Omdat ze ons niet altijd zullen vragen naar de kracht die door de zwaartekracht wordt gegenereerd, kunnen ze ons ook vragen de afstand tussen de twee lichamen, of een van de massa’s, te berekenen. Al moet je de drie onderstaande formules niet uit je hoofd leren, omdat je ze kunt afleiden uit de eerste die we je hebben geleerd.
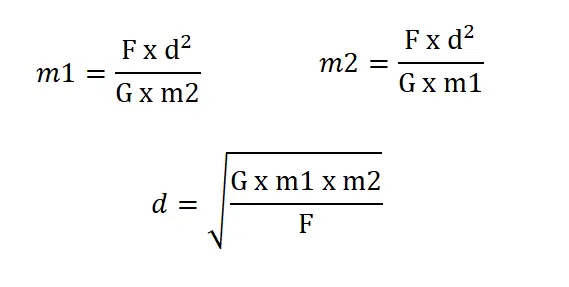
aantrekkingskracht tussen verschillende lichamen
Als we de aantrekkingskracht tussen meer dan twee objecten willen berekenen, kunnen we niet onze toevlucht nemen tot de formule waar we eerder commentaar op gaven, omdat we dan variabelen zouden missen. Daarom is het noodzakelijk om de zwaartekracht ten opzichte van een van de massa’s te berekenen met behulp van een andere methode. We doen dit door de aantrekkingskracht van alle lichamen toe te voegen . Om het duidelijker te maken, moeten we de volgende formule volgen:
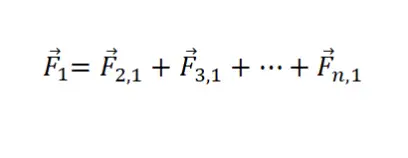
In principe moeten we met de zwaartekrachtformule waar we in het begin commentaar op gaven, de aantrekkingskracht berekenen van alle lichamen die het systeem vormen in relatie tot een bepaalde massa . In het geval van het voorbeeld gebruiken we massa 1. Zodra je als je de waarden van alle krachten hebt, tel je ze eenvoudig bij elkaar op. Zo krijg je de zwaartekracht die op de betreffende massa inwerkt. Deze wiskundige procedure kan worden toegepast op sets van maximaal oneindige massa’s.
Conclusies over zwaartekracht
Samenvattend kunnen we zeggen dat de zwaartekracht rechtstreeks afhangt van de massa’s en omgekeerd evenredig is met het kwadraat van de afstand. Dat kan rechtstreeks worden afgeleid via de wiskundige formule die we aan het begin van dit artikel noemden.
Ten slotte willen we ook een formule toevoegen waarmee we de intensiteit van het zwaartekrachtveld of de versnelling van de zwaartekracht op een bepaald punt kunnen kennen. Deze uitdrukking komt uit de formule voor universele zwaartekracht en de formule voor de tweede wet van Newton (F = mxa). Hieronder ziet u wat wij bedoelen.
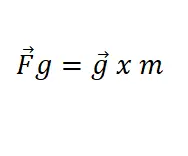
zwaartekracht van de aarde
Daarnaast willen we uitleggen dat de waarde van de zwaartekracht van de aarde de versnelling is die objecten ontvangen van planeet Aarde. Deze versnelling wordt gevormd door de som van de aantrekkingskracht die door de planeet wordt gegenereerd en de centrifugaal- of rotatiekracht van de planeet. De exacte waarde van de zwaartekracht van de aarde is gelijk aan 9,80665 m/s 2 of 1 g . Dit komt omdat g gelijk is aan de zwaartekracht van de aarde.
Wanneer we de aantrekkingskracht tussen de aarde en een ander lichaam berekenen, moeten we er rekening mee houden dat de afstand de som is van de straal van de planeet plus de hoogte waarop het object zich bevindt. Dit is iets dat veel mensen vergeten, maar het is belangrijk om de twee afstanden bij elkaar op te tellen voordat je de zwaartekrachtformule toepast, anders is het resultaat onjuist.