Op deze pagina ontdek je wat de wortels van een polynoom zijn en hoe ze worden berekend. Bovendien kun je voorbeelden en oefeningen zien die stap voor stap zijn opgelost op basis van de wortels van een polynoom.
Wat zijn de wortels van een polynoom?
In de wiskunde zijn de wortels (of nullen) van een polynoom de waarden die de polynoom opheffen. Dat wil zeggen, de wortels van een polynoom zijn al die waarden die, wanneer ze in de polynoom worden geëvalueerd, een numerieke waarde gelijk aan 0 hebben.
Eventueel,
![]()
is een wortel van de polynoom
![]()
Ja
![]()
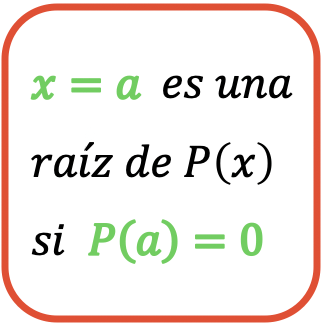
Als we bijvoorbeeld de volgende polynoom hebben:
![]()
We kunnen verifiëren dat een van de wortels van de polynoom 1 is, aangezien de numerieke waarde van de polynoom op x=1 gelijk is aan nul:
![]()
Aan de andere kant is 3 geen wortel van de polynoom omdat het geen waarde is die de polynoom annuleert, of met andere woorden: de numerieke waarde van de polynoom op x=3 verschilt van nul:
![]()
Waarschijnlijk begrijp je nu beter wat de wortel van een polynoom is, maar zou je niet graag willen weten hoeveel wortels een polynoom heeft? Of hoe vind je alle wortels van een polynoom? Welnu, dat is precies wat we in de volgende sectie gaan zien.
Hoe bereken je alle wortels van een polynoom?
Om alle wortels van een polynoom te vinden, moet je de volgende stappen volgen:
- Eerst worden alle delers van de onafhankelijke term van de polynoom berekend.
- Ten tweede worden alle waarden die in de vorige stap zijn gevonden, geëvalueerd in de polynoom.
- Tenslotte, als bij het evalueren van een getal in de polynoom de numerieke waarde ervan gelijk is aan nul, is dat getal een wortel van de polynoom. Anders komt het genoemde getal niet overeen met een wortel van de polynoom.
Deze procedure is afgeleid van de reststelling . Klik op deze link om de reden voor deze specifieke procedure te achterhalen.
Voorbeeld van het berekenen van de wortels van een polynoom
Hieronder zullen we stap voor stap een voorbeeld oplossen, zodat u beter begrijpt hoe u de wortels van een polynoom kunt nemen.
- Wat zijn alle wortels van de volgende polynoom?
![]()
Allereerst moeten we de delers van de onafhankelijke term vinden, omdat elke wortel van een polynoom ook een deler van de onafhankelijke term is. De delers van 6 zijn dus:
Delers van 6: +1, -1, +2, -2, +3, -3
Onthoud dat als een getal een deler is, het negatieve getal ook een deler is. Omdat een getal deelbaar is door positieve en negatieve getallen.
De mogelijke wortels of nulpunten van de polynoom zijn dus: ±1, ±2, ±3. Daarom moeten we de numerieke waarde van de polynoom voor al deze waarden bepalen. En om dit te doen, vervangen we deze waarden in de uitdrukking van de polynoom waar een x staat:
![]()
![]()
![]()
![]()
![]()
![]()
De polynoom verdwijnt dus alleen als de variabele x +2 of +3 is, dus hier zijn de wortels van de polynoom:
Wortels of nulpunten van de polynoom : +2 en +3
Merk aan de andere kant op dat de polynoom evenveel wortels heeft als zijn graad, dat wil zeggen dat aangezien de polynoom van de tweede graad is, hij twee wortels heeft. Bij de eigenschappen van de wortels van een polynoom (hieronder) zullen we zien waarom dit kenmerk altijd geldt voor elke polynoom.
We hebben zojuist een manier gezien om de wortels van een polynoom te vinden. Er zijn echter nog andere methoden om dit te bereiken, je kunt bijvoorbeeld ook de wortels van een polynoom vinden met de regel van Ruffini. Klik op de volgende link om voorbeelden van de Ruffini-regel te zien, hier ontdekt u waaruit deze bekende methode bestaat en ook wat de verschillen zijn tussen de twee procedures.
Eigenschappen van de wortels van een polynoom
De wortels of nulpunten van een polynoom hebben de volgende kenmerken:
- Zoals we eerder hebben gezien, zijn de gehele wortels (of nullen) van een polynoom delers van de onafhankelijke term van de polynoom.
- Als we alle wortels van een polynoom kennen, kunnen we deze polynoom uitdrukken in de vorm van producten van binomiale getallen van het type
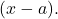
Bijvoorbeeld de polynoom
![]()
Het heeft 3 wortels
![]()
En
![]()
We kunnen de polynoom daarom herschrijven in de vorm van 3 vermenigvuldigingen van factoren, elk gevormd door de variabele
![]()
en een wortel is van teken veranderd:
![Rendered by QuickLaTeX.com \displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce071610927d2723c8ac2e7b299c1c5d_l3.png)
![]()
Dit wordt polynomiale factoring genoemd. Een van de belangrijkste toepassingen van het bepalen van de wortels van een polynoom is dat ze worden gebruikt om deze in factoren te ontbinden. In de volgende link leest u waaruit deze bijzondere bewerking bestaat en daarnaast kunt u oefenen met opgeloste polynomiale ontbindingsoefeningen .
- Een polynoom heeft zoveel wortels als de graad aangeeft. Een polynoom van de tweede graad heeft dus twee wortels, een polynoom van de derde graad heeft drie wortels, een polynoom van de vierde graad heeft vier wortels, enzovoort.
- Als een polynoom geen onafhankelijke term heeft, betekent dit dat een van zijn wortels 0 is. Dan moeten de rest van de wortels delers zijn van de coëfficiënt van de monomiaal van de laagste graad.
De volgende polynoom heeft bijvoorbeeld geen onafhankelijke term:
![]()
Eén wortel van de polynoom moet dus noodzakelijkerwijs 0 zijn. En de rest van de wortels zijn delers van de coëfficiënt van de term van de laagste graad, dat wil zeggen -2. Om precies te zijn, de andere wortels zijn dat ook
![]()
En
![]()
dus alle wortels van de polynoom zijn:
Wortels of nullen van de polynoom: 0, +1 en -2
- Wanneer de wortels van een polynoom niet kunnen worden bepaald, wordt er gezegd dat het een irreducibele polynoom is.
We zullen bijvoorbeeld proberen de wortels van de volgende polynoom te berekenen:
![]()
De enige mogelijke wortels van de polynoom zijn de delers van -1, dat wil zeggen -1 en +1. We evalueren daarom de polynoom met deze waarden:
![]()
![]()
In geen geval wordt het polynoom geannuleerd, dus het heeft geen wortels en is daarom een onherleidbaar polynoom.
- Wanneer de polynoom bestaat uit het product van verschillende polynomen, is het niet nodig om dit product te gebruiken om de wortels te berekenen, maar de wortels van de polynoom zijn de wortels van elke vermenigvuldigde factor.
Als we bijvoorbeeld de volgende polynoom hebben:
![]()
Uit de tweede eigenschap van de wortels van polynomen kunnen we afleiden dat de wortel van het linker polynoom +2 is en de wortel van het rechter polynoom -1.
![]()
![]()
De wortels van de polynoom die voortkomen uit de vermenigvuldiging van de twee factoren zijn dus hun respectieve wortels, dwz +2 en -1.
![Rendered by QuickLaTeX.com \displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-416399918b5a2a051a6bfc7343ef7960_l3.png)
Opgeloste oefeningen over de wortels van veeltermen
Oefening 1
Bepaal of
![]()
is een wortel van de volgende polynoom:
![]()
Om erachter te komen of
![]()
een wortel is van de polynoom, moeten we deze op die waarde evalueren. Nog:
![Rendered by QuickLaTeX.com \begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c88c4456693b0c57d55aba68287414c_l3.png)
De numerieke waarde van de polynoom in
![]()
nul is, dus het is in feite een wortel van de polynoom.
Oefening 2
Bereken alle wortels van de volgende polynoom:
![]()
Om de mogelijke wortels van de polynoom te vinden, moeten we eerst de delers van de onafhankelijke term vinden. De delers van 2 zijn dus:
Delers van 2: +1, -1, +2, -2
De mogelijke wortels of nulpunten van de polynoom zijn daarom ±1 en ±2. Daarom moeten we berekenen hoeveel de polynoom in al deze waarden is:
![]()
![]()
![]()
![]()
Het polynoom verdwijnt dus wanneer x +1 of +2 is, dus hier zijn de wortels van het polynoom:
Wortels of nulpunten van de polynoom : +1 en +2
Oefening 3
Zoek de wortels van de volgende polynoom:
![]()
We moeten eerst de delers van de onafhankelijke term vinden, aangezien de wortel van een polynoom ook een deler van de onafhankelijke term is. De delers van 4 zijn dus:
Delers van 4: +1, -1, +2, -2, +4, -4
De mogelijke wortels of nulpunten van de polynoom zijn daarom ±1, ±2 en ±4. We moeten daarom de numerieke waarde van de polynoom in al deze waarden vinden:
![]()
![]()
![]()
![]()
![]()
![]()
Het polynoom verdwijnt dus alleen als x +1, +2 of -2 is, dus hier zijn de wortels van het polynoom:
Wortels of nulpunten van de polynoom : +1, +2 en -2
Oefening 4
Zoek de wortels van de volgende polynoom:
![]()
In dit geval heeft de polynoom geen onafhankelijke term. Daarom weten we, volgens de vierde eigenschap van wortels die hierboven is uitgelegd, dat een van de wortels van de polynoom 0 moet zijn.
Wortels van de polynoom:
![]()
Bovendien zijn de mogelijke wortels in dit geval niet de delers van de onafhankelijke term, maar eerder die van de coëfficiënt van de term van de laagste graad, namelijk 8:
Delers van 8: +1, -1, +2, -2, +4, -4, +8, -8
De mogelijke wortels of nulpunten van de polynoom zijn dus ±1, ±2, ±4 en ±8. We moeten daarom de numerieke waarde van de polynoom bij al deze waarden berekenen:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
De polynoom verdwijnt dus als x +2 of +4 is, dus deze waarden zijn de wortels van de polynoom. We moeten echter ook de root 0 toevoegen die we aan het begin van het probleem hebben gevonden. Concluderend zijn alle wortels van de polynoom:
Wortels of nulpunten van de polynoom : 0, +2 en +4
Oefening 5
Gebruik de eigenschappen van wortels van polynomen om de wortels van de volgende polynoom te berekenen:
![]()
Zoals we bij de zesde eigenschap van wortels hebben gezien, is het niet nodig om alle wortels te berekenen als de polynoom wordt gevormd door het product van factoren, aangezien de wortels van de gehele polynoom de wortels van elke factor zijn.
Bovendien kunnen we uit de tweede eigenschap van de wortels van polynomen afleiden dat de wortel van de eerste factor +1 is en de wortel van de tweede factor -3.
![]()
![]()
We hoeven dus alleen maar de wortels van de laatste factor te vinden. Om dit te doen, vinden we de delers van de onafhankelijke term (-2):
Delers van -2: +1, -1, +2, -2
De mogelijke wortels of nulpunten van de laatste polynoom zijn dus ±1 en ±2. Waarmee we de numerieke waarde van genoemde polynoom in al deze waarden moeten berekenen:
![]()
![]()
![]()
![]()
![]()
De wortels van de polynoom aan de rechterkant zijn dus -1 en 2.
Daarom zijn de wortels van de gehele polynoom alle gevonden wortels:
Wortels of nullen van de polynoom : +1, -1, +2, -3