In dit artikel zullen we zien hoe we elk type functie in een grafiek kunnen weergeven. Daarnaast vind je opgeloste stap-voor-stap oefeningen over het weergeven van functies in een grafiek.
Hoe een functie in een grafiek weer te geven
Om een functie in een grafiek weer te geven, moeten de volgende stappen worden uitgevoerd:
- Zoek het domein van de functie.
- Bereken de afkappunten van de functie met de cartesiaanse assen.
- Bereken de asymptoten van de functie.
- Bestudeer de monotoniciteit van de functie en vind de relatieve uitersten ervan.
- Bestudeer de kromming van de functie en vind de buigpunten .
- Zet de afkappunten, asymptoten, relatieve extrema en buigpunten in kaart en plot vervolgens de functie.
Voorbeeld van het weergeven van een functie
Zodat je kunt zien hoe een functie grafisch wordt weergegeven, gaan we de volgende oefening stap voor stap oplossen:
- Teken de volgende rationale functie in een grafiek:
![]()
Het eerste dat u moet doen, is het domein van de functie berekenen . Dit is een rationale functie, dus we moeten de noemer gelijk stellen aan nul om te zien welke getallen niet tot het domein van de functie behoren:
![]()
![]()
Dus als x 1 is, zal de noemer 0 zijn en daarom zal de functie niet bestaan. Het domein van de functie bestaat dus uit alle reële getallen behalve x=1.
![]()
Om het snijpunt met de X-as te vinden, moeten we de vergelijking oplossen
![]()
Omdat de functie op de X-as altijd de waarde 0 heeft:
![]()
![]()
De voorwaarde
![]()
Dit houdt in dat we de hele linkerkant delen, zodat we deze met de hele rechterkant kunnen vermenigvuldigen:
![]()
![]()
![]()
Het snijpunt met de OX-as is daarom:
![]()
En om het snijpunt met de Y-as te vinden, berekenen we
![]()
Omdat x altijd 0 is op de Y-as:
![]()
Daarom is het afkappunt met de OY-as:
![]()
In dit geval, wanneer de functie door de coördinaatoorsprong gaat, valt het snijpunt met de X-as samen met het snijpunt met de Y-as.
Zodra we het domein en de afkappunten kennen, moeten we de asymptoten van de functie berekenen .
Om te zien of de functie verticale asymptoten heeft, moeten we de limiet van de functie berekenen op punten die niet tot het domein behoren (in dit geval x=1). En als het resultaat oneindig is, is het een verticale asymptoot. Nog:
![]()
Omdat de limiet van de functie wanneer x naar 1 neigt oneindigheid oplevert, is x = 1 een verticale asymptoot:
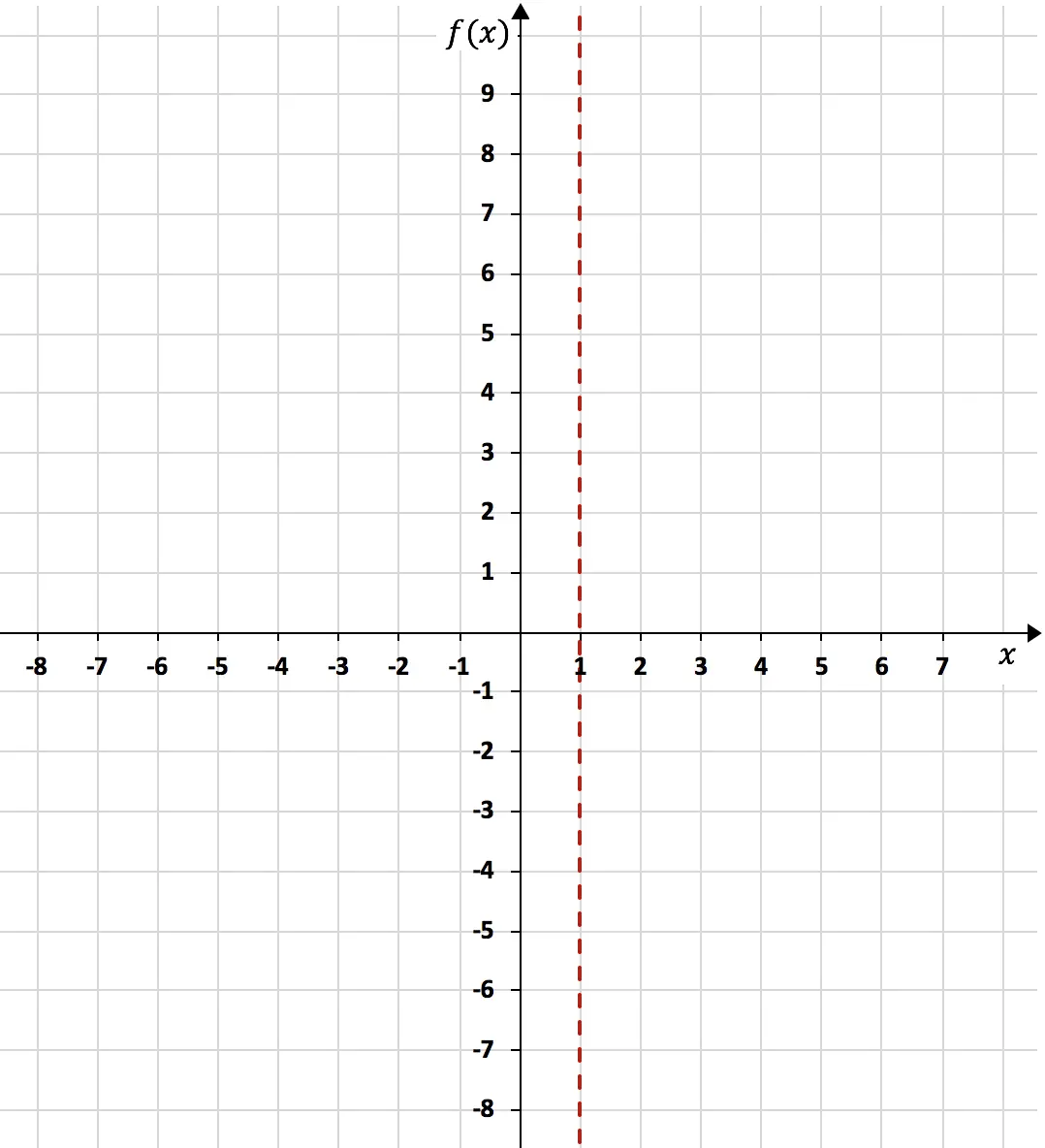
Nadat de verticale asymptoot is berekend, is het noodzakelijk om de laterale grenzen van de functie ten opzichte daarvan te berekenen. Omdat we niet weten of de functie de neiging zal hebben om -∞ of +∞ te benaderen als hij x=1 van links benadert, en we niet weten wanneer hij x=1 van rechts benadert.
We gaan dus verder met het berekenen van de linker laterale limiet van de functie op x=1:
![]()
Om numeriek een laterale grens op een punt te berekenen, moeten we een getal in de functie vervangen dat heel dicht bij het punt ligt. In dit geval willen we een getal dat heel dicht bij 1 ligt aan de linkerkant, zoals 0,9. We vervangen daarom het punt 0.9 in de functie:
![]()
Laterale grenzen aan een asymptoot kunnen alleen +∞ of -∞ opleveren. En omdat we door een getal dat heel dicht bij 1 ligt aan de linkerkant te vervangen door de functie een negatief resultaat kregen, is de limiet aan de linkerkant -∞:
![]()
Nu doen we dezelfde procedure met de rechterzijgrens:
![]()
We vervangen een getal dat heel dicht bij 1 ligt aan de rechterkant in de functie. Bijvoorbeeld punt 1.1:
![]()
In dit geval is het zijlimietresultaat een positief getal. De limiet aan de rechterkant is daarom +∞:
![]()
Concluderend: bij x=1 neigt de functie naar min oneindig aan de linkerkant, en plus oneindig aan de rechterkant:
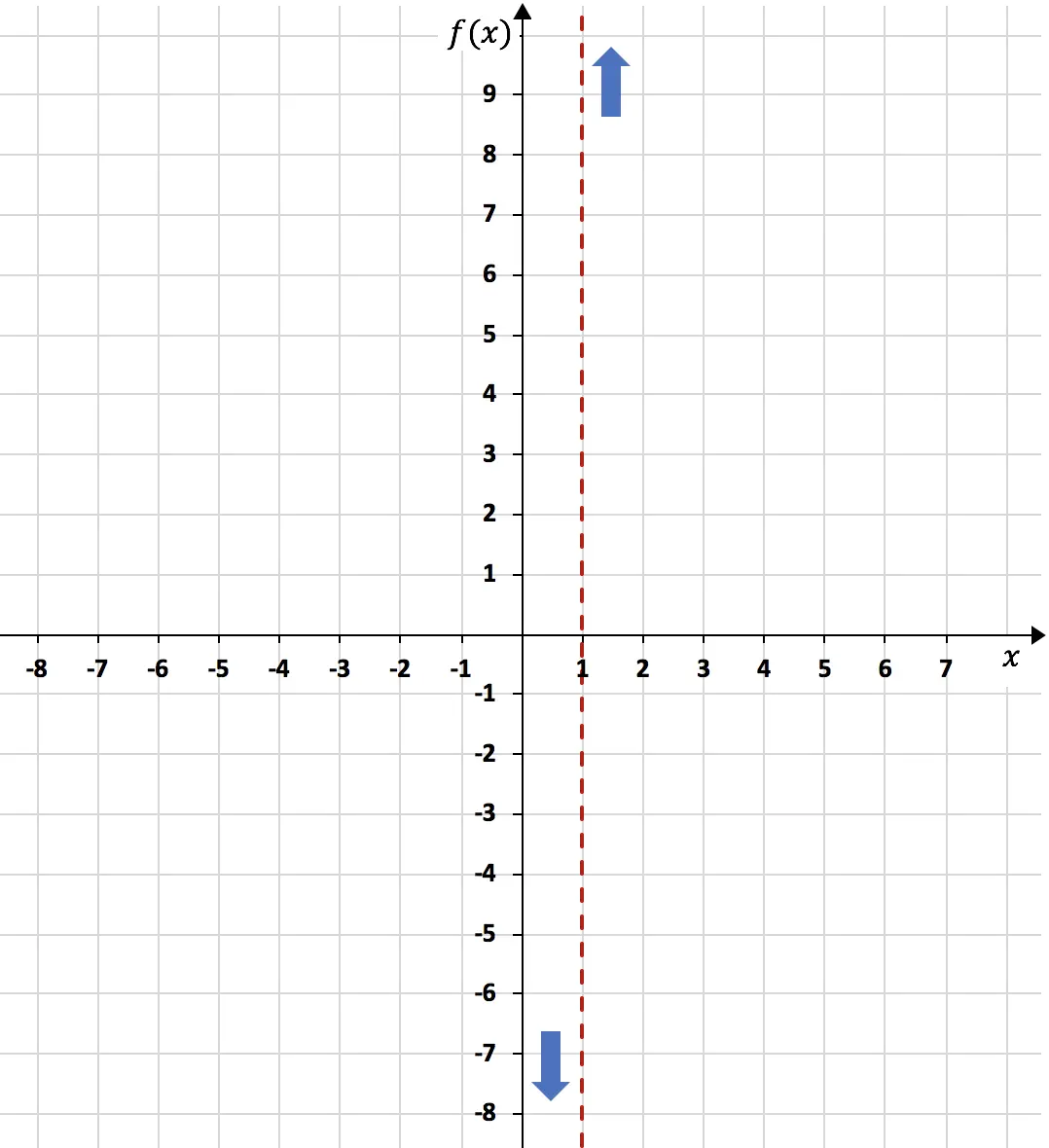
Aan de andere kant zal de horizontale asymptoot van de functie het resultaat zijn van de oneindige limiet van de functie. Nog:
![]()
Onthoud hoe je de oneindige grenzen van rationale functies berekent:
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
</div>
<p> De oneindige limiet van de functie gaf ons +∞, dus de functie heeft geen horizontale asymptoot.</p>
<p> We berekenen nu de schuine asymptoot. De schuine asymptoten hebben de vorm</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
. EN
![]()
Het wordt berekend met de volgende formule:
![]()
![]()
De x is alsof hij een 1 als noemer heeft:
![]()
Het is een deling van breuken, dus we vermenigvuldigen ze in de dwarsrichting:
![]()
![]()
En we berekenen de limiet:
![]()
Dus m=1. Nu gaan we berekenen
![]()
met de volgende formule:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
Maar we krijgen de onbepaaldheid oneindig min oneindig, dus we moeten de termen terugbrengen tot een gemeenschappelijke noemer. Om dit te doen, vermenigvuldigen en delen we de term x door de noemer van de breuk:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
Nu de twee termen dezelfde noemer hebben, kunnen we ze groeperen:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
En tenslotte lossen we de limiet op:
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
Dus n = 1. De schuine asymptoot is daarom:
![]()
![]()
![]()
Nadat we de schuine asymptoot hebben berekend, geven we deze weer in dezelfde grafiek door een tabel met waarden te maken:
![]()

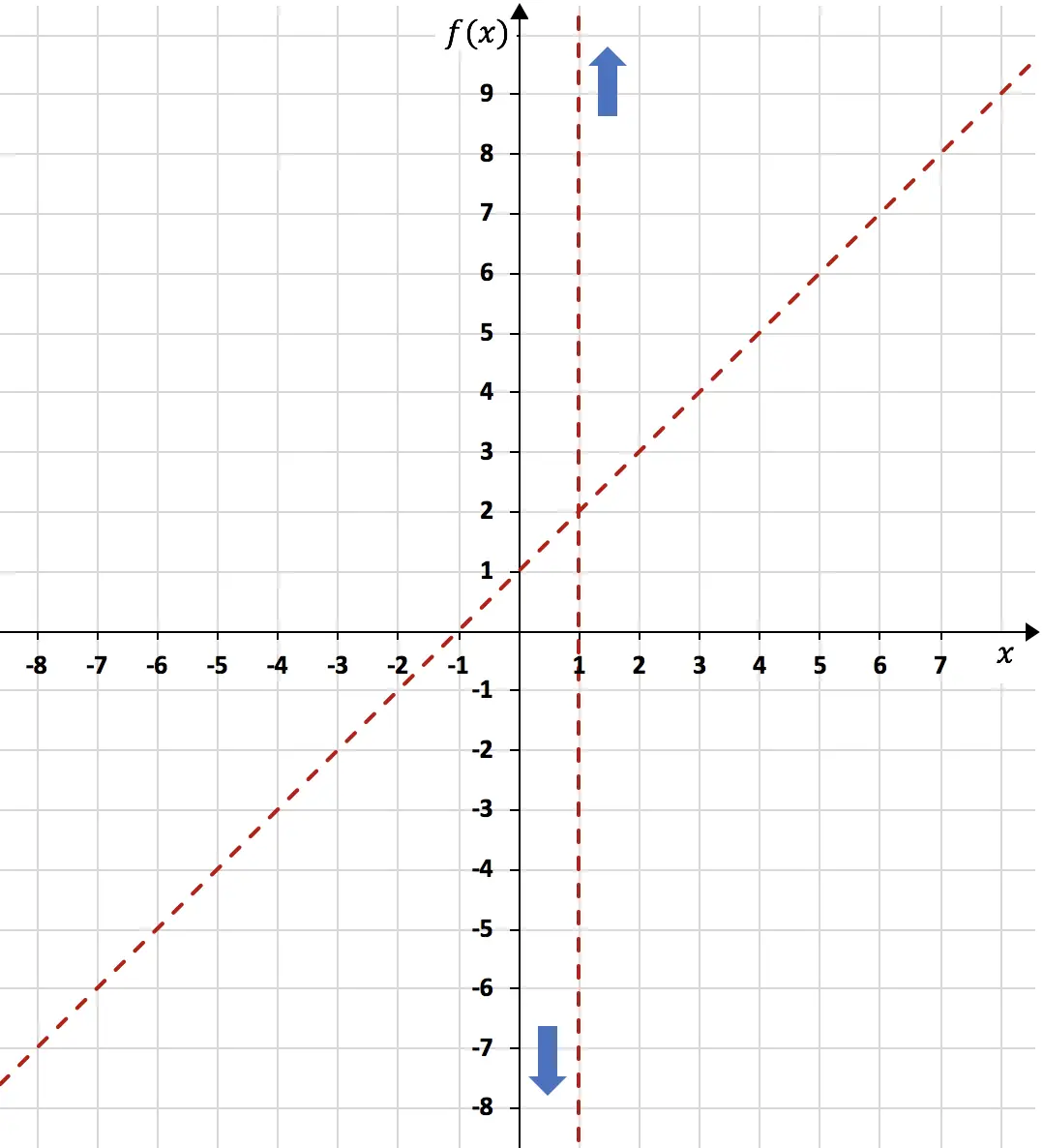
Nu we alle asymptoten van de functie kennen, moeten we de monotoniciteit van de functie analyseren. Dat wil zeggen dat we moeten bestuderen in welke intervallen de functie toeneemt en in welke intervallen deze afneemt. We berekenen daarom de eerste afgeleide van de functie:
![]()
![]()
En nu stellen we de afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
De voorwaarde
![]()
Dit houdt in dat we de hele linkerkant delen, zodat we deze met de hele rechterkant kunnen vermenigvuldigen:
![]()
![]()
We extraheren de gemeenschappelijke factor om de kwadratische vergelijking op te lossen:
![]()
Om de vermenigvuldiging gelijk te maken aan 0, moet een van de twee elementen van de vermenigvuldiging nul zijn. Daarom stellen we elke factor gelijk aan 0 en verkrijgen we beide oplossingen van de vergelijking:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
We geven nu op de getallenlijn alle gevonden kritische punten weer, dat wil zeggen de punten die niet tot het domein behoren (x=1) en de punten die de afgeleide opheffen (x=0 en x=2):

En we evalueren het teken van de afgeleide in elk interval, om te weten of de functie toeneemt of afneemt. We nemen daarom in elk interval een punt (nooit de kritische punten) en kijken welk teken de afgeleide op dat punt heeft:
![]()
![]()
![]()
![]()
![]()
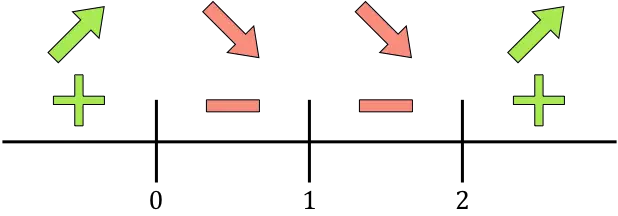
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en afname-intervallen:
Groei:
![]()
Afname:
![]()
Bovendien gaat de functie bij x=0 van stijgend naar dalend, dus x=0 is een relatief maximum van de functie. En bij x=2 gaat de functie van afnemend naar toenemend, dus x=2 is een relatief minimum van de functie.
Ten slotte vervangen we de gevonden uitersten in de oorspronkelijke functie om de Y-coördinaat van de punten te vinden:
![]()
![]()
De relatieve uitersten van de functie zijn daarom:
Maximaal op punt
![]()
Minimaal tot punt
![]()
We vertegenwoordigen het maximum en minimum in de grafiek:
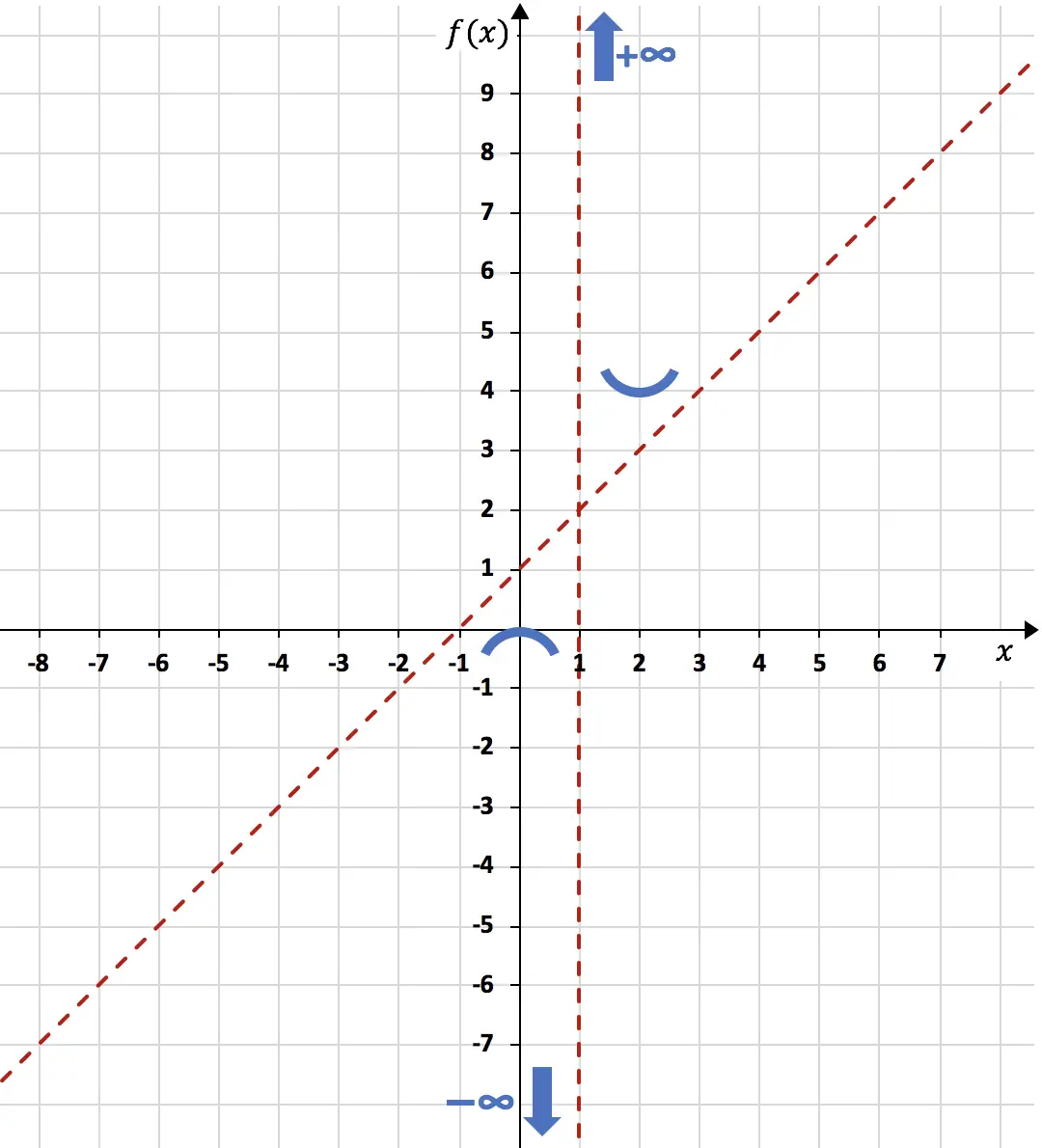
Ten slotte is het voldoende om de kromming van de functie te bestuderen , dat wil zeggen om de intervallen van concaafheid en convexiteit van de functie te bestuderen. Om dit te doen, berekenen we de tweede afgeleide:
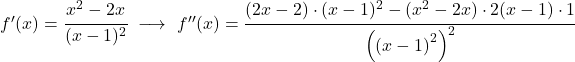
![]()
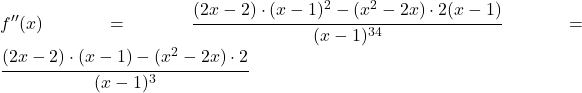
![]()
![]()
En nu stellen we de tweede afgeleide gelijk aan nul en lossen we de vergelijking op:
![]()
![]()
![]()
![]()
2 zal nooit gelijk zijn aan 0, dus de vergelijking
![]()
Er is geen oplossing.
We geven nu op de getallenlijn alle gevonden kritische punten weer, dat wil zeggen de punten die niet tot het domein behoren (x=1) en de punten die de tweede afgeleide opheffen (in dit geval zijn er geen punten die niet bestaan):

En we evalueren het teken van de afgeleide in elk interval, om te weten of de functie convex of concaaf is. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
![]()

En tenslotte leiden we de intervallen van concaviteit en convexiteit van de functie af. Als de tweede afgeleide positief is, betekent dit dat de functie convex is.
![]()
, en als de tweede afgeleide negatief is, betekent dit dat de functie concaaf is
![]()
. De concaviteits- en convexiteitsintervallen zijn daarom:
Convex
![]()
:
![]()
Concaaf
![]()
:
![]()
Hoewel er echter een verandering in de kromming optreedt op x=1, is dit geen buigpunt. Omdat x=1 niet tot het domein van de functie behoort.
We kunnen dus de functie representeren met behulp van alles wat we hebben berekend:
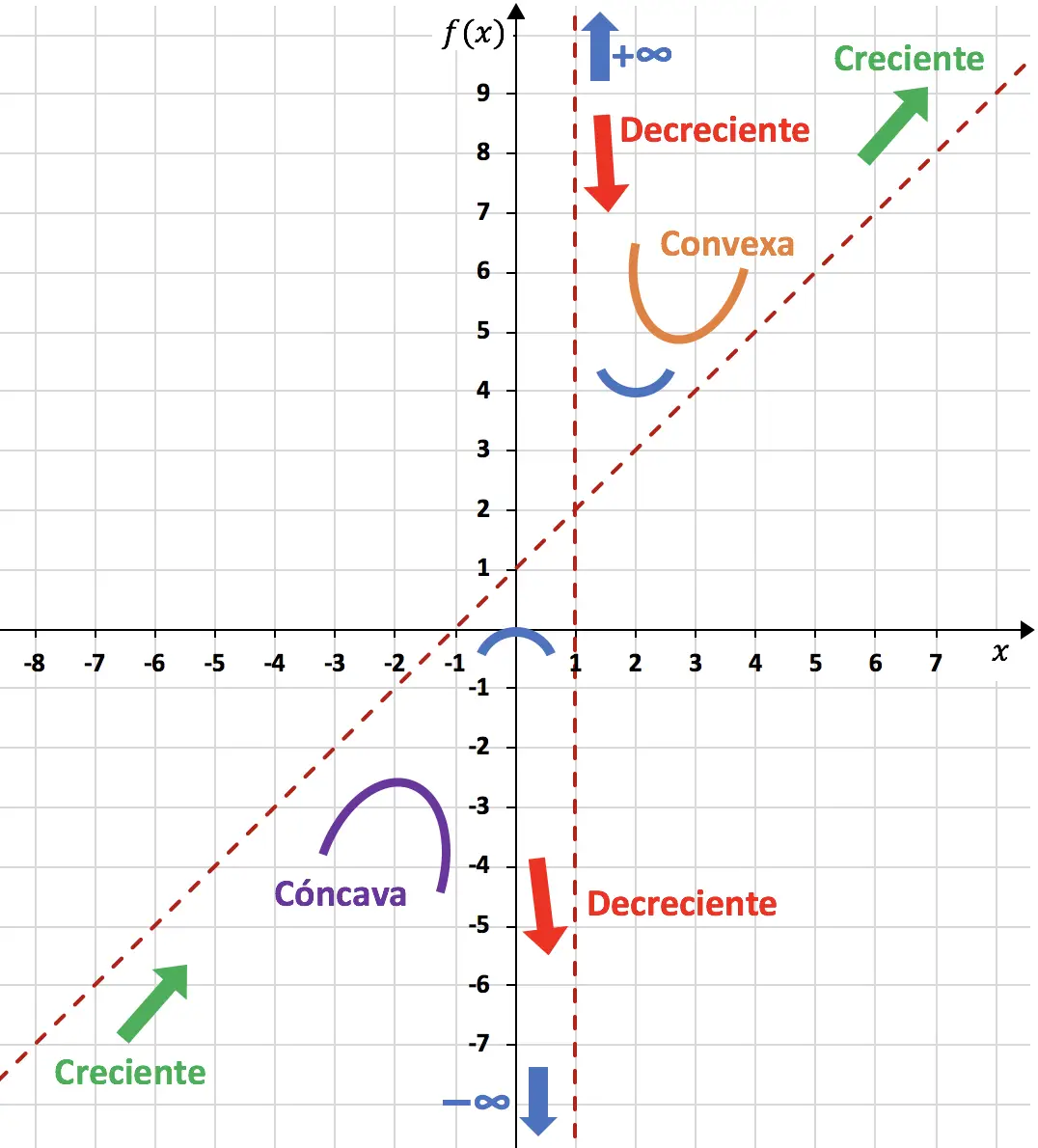
De in de grafiek weergegeven functie ziet er daarom als volgt uit:
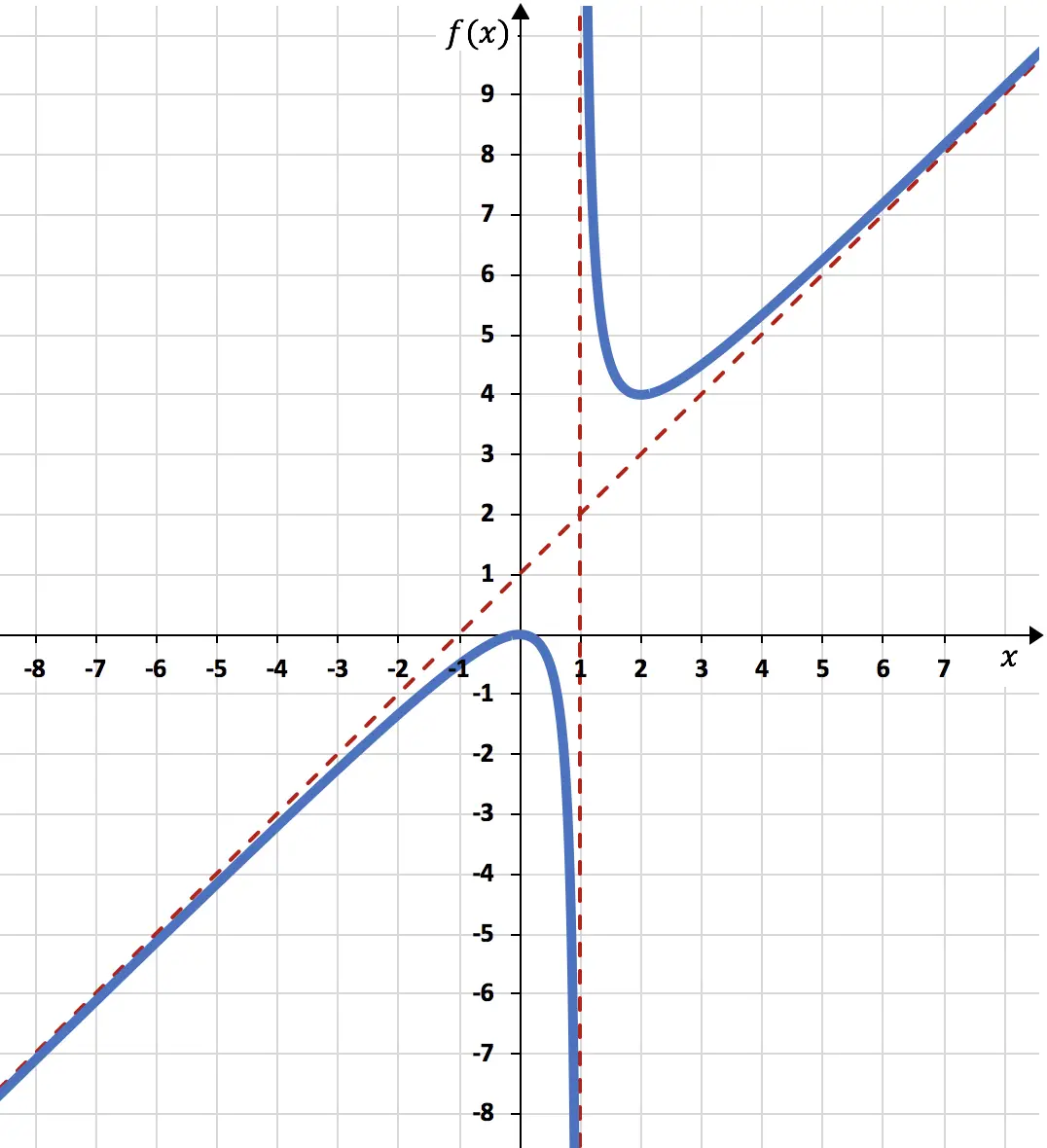
Opgeloste oefeningen om functies weer te geven
Oefening 1
Teken de volgende polynomiale functie:
![]()
Het eerste dat u moet doen, is het domein van de definitie van de functie berekenen. Dit is een polynoomfunctie, dus het domein bestaat alleen uit reële getallen:
![]()
Om het snijpunt met de X-as te vinden, lossen we op
![]()
![]()
![]()
Dit is een graadvergelijking groter dan 2. Daarom factoriseren we de vergelijking:
![]()
Dus x=-1 is een oplossing. En we berekenen de andere oplossingen door de resulterende kwadratische vergelijking op te lossen:
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
De snijpunten met de X-as zijn daarom:
![]()
En
![]()
En om het snijpunt met de Y-as te vinden, berekenen we
![]()
Omdat x altijd 0 is op de Y-as:
![]()
Het snijpunt met de Y-as is dus:
![]()
Om te zien of de functie verticale asymptoten heeft, moeten we de limiet van de functie berekenen op punten die niet tot het domein behoren. In dit geval omvat het domein alle reële getallen. De functie heeft dus geen verticale asymptoot.
Aan de andere kant zal de horizontale asymptoot van de functie het resultaat zijn van de oneindige limiet van de functie. Nog:
![]()
De oneindige limiet van de functie gaf ons +∞, dus de functie heeft geen horizontale asymptoot.
We berekenen nu de schuine asymptoot. De schuine asymptoten hebben de vorm
![]()
EN
![]()
Het wordt berekend met de volgende formule:
![]()
![]()
De limiet gaf ons +∞, dus de functie heeft ook geen schuine asymptoot.
Om de monotoniciteit van de functie te bestuderen, moeten we eerst de afgeleide berekenen:
![]()
Nu stellen we de afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
We geven nu op de getallenlijn alle verkregen singuliere punten weer, dat wil zeggen de punten die niet tot het domein behoren (in dit geval horen ze er allemaal bij) en de punten die de afgeleide opheffen (x=0 en x =2). :

En we evalueren het teken van de afgeleide in elk interval, om te weten of de functie toeneemt of afneemt. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
![]()

Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en afname-intervallen:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend bij x=0, dus x=0 is een maximum van de functie. En de functie gaat van afnemend naar toenemend bij x=2, dus x=2 is een minimum van de functie.
Ten slotte vervangen we de gevonden uitersten in de oorspronkelijke functie om de Y-coördinaten van de punten te vinden:
![]()
![]()
De relatieve uitersten van de functie zijn daarom:
Maximaal op punt
![]()
Minimaal tot punt
![]()
Om de kromming van de functie te bestuderen, berekenen we de tweede afgeleide:
![]()
Nu stellen we de tweede afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
![]()
![]()
We vertegenwoordigen op de lijn alle gevonden singuliere punten, dat wil zeggen de punten die niet tot het domein behoren (in dit geval horen ze allemaal) en de punten die de afgeleide opheffen (x=1):

En nu evalueren we het teken van de tweede afgeleide in elk interval, om te weten of de functie concaaf of convex is. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de tweede afgeleide op dit punt heeft:
![]()
![]()

Als de tweede afgeleide positief is, betekent dit dat de functie convex is.
![]()
, en als de tweede afgeleide negatief is, betekent dit dat de functie concaaf is
![]()
. De concaviteits- en convexiteitsintervallen zijn daarom:
Convex
![]()
:
![]()
Concaaf
![]()
:
![]()
Bovendien verandert de functie van concaaf naar convex bij x=1, dus x=1 is een buigpunt van de functie.
Ten slotte vervangen we de gevonden buigpunten in de oorspronkelijke functie om de Y-coördinaat van de punten te vinden:
![]()
De keerpunten van de functie zijn daarom:
Keerpunten:
![]()
Ten slotte tekenen we, op basis van alle informatie die we hebben berekend, de functie:
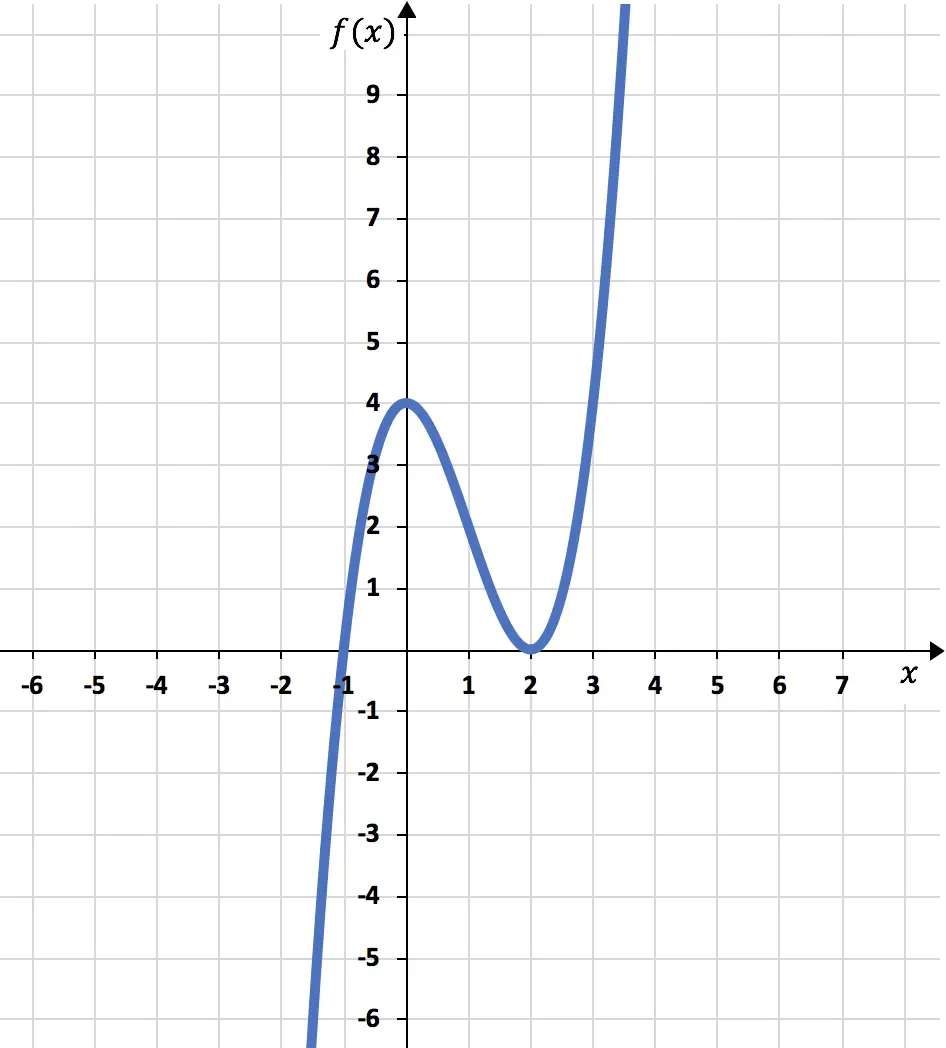
Oefening 2
Grafiek de volgende rationale functie:
![]()
Om het domein van de functie te vinden, stellen we de noemer gelijk. breng de breuk naar nul en los de resulterende vergelijking op:
![]()
![]()
![]()
![]()
![]()
Ten tweede bepalen we de drempels van de functie waarbij de x-as gelijk is aan de algebraïsche uitdrukking van de functie. staal:
![]()
![]()
![]()
![]()
![]()
![]()
Er is geen vierkantswortel van een negatief getal. Daarom snijdt de functie de X-as niet.
En om het snijpunt met de computeras te vinden, evalueren we de functie op x=0.
![]()
Het snijpunt met de Y-as is dus:
![]()
Om te zien of de functie verticale asymptoten heeft, moeten we de limiet van de functie berekenen op punten die niet tot het domein behoren (in dit geval x=-1 en x=+1). En als het resultaat oneindig is, is het een verticale asymptoot. Nog:
![]()
Omdat de limiet van de functie wanneer x -1 nadert, oneindigheid oplevert, is x = -1 een verticale asymptoot.
We berekenen de laterale grenzen van de asymptoot x=-1 door een getal dat er heel dichtbij ligt in de functie te vervangen:
![]()
![]()
Laten we nu eens kijken of x=+1 een verticale asymptoot is:
![]()
Omdat de limiet van de functie wanneer x +1 nadert, oneindigheid oplevert, is x=+1 een verticale asymptoot.
We berekenen de laterale grenzen van de asymptoot x=1 door een getal dat er heel dicht bij ligt in de functie te vervangen:
![]()
![]()
Aan de andere kant zal de horizontale asymptoot van de functie het resultaat zijn van de oneindige limiet van de functie. Nog:
![]()
De oneindige limiet van de functie gaf ons 1, dus de functie heeft een horizontale asymptoot op y=1.
Omdat de functie een horizontale asymptoot heeft, zal deze geen schuine asymptoot hebben.
We differentiëren de functie en bestuderen vervolgens de intervallen van groei en afname:
![]()
![]()
Nu stellen we de afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
![]()
![]()
![]()
We geven op de lijn alle berekende kritische punten weer, namelijk de punten die niet tot het domein behoren (x=-1 en x=+1) en de punten die de afgeleide opheffen (x=0):

En we evalueren het teken van de afgeleide in elk interval, om te weten of de functie toeneemt of afneemt. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
![]()
![]()
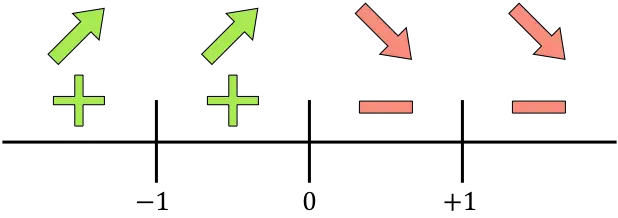
De functie neemt toe als de afgeleide positief is en de functie neemt af als de functie negatief is:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend bij x=0, dus x=0 is een lokaal maximum van de functie.
We vervangen het gevonden extremum in de oorspronkelijke functie om de Y-coördinaat van het punt te vinden:
![]()
De relatieve uitersten van de functie zijn daarom:
Maximaal op punt
![]()
Om de kromming van de functie te bestuderen, berekenen we de tweede afgeleide:
![f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png) Alle termen hebben
Alle termen hebben
![]()
, kunnen we daarom de breuk vereenvoudigen:
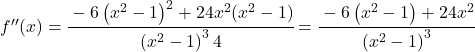
![]()
Nu stellen we de tweede afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Er is geen vierkantswortel van een negatief getal. Er is dus geen enkel punt dat overeenkomt
![]()
Nu vertegenwoordigen we op de lijn alle gevonden singuliere punten, dat wil zeggen de punten die niet tot het domein behoren (x=-1 en x=+1) en die welke de tweede afgeleide opheffen (in dit geval zijn er geen elk):
En we evalueren het teken van de tweede afgeleide in elk interval, om te weten of de functie concaaf of convex is. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de tweede afgeleide op dit punt heeft:
![]()
![]()
![]()

Als de tweede afgeleide positief is, betekent dit dat de functie convex is.
![]()
, en als de tweede afgeleide negatief is, betekent dit dat de functie concaaf is
![]()
. De concaviteits- en convexiteitsintervallen zijn daarom:
Convex
![]()
:
![]()
Concaaf
![]()
:
![]()
Hoewel er echter een verandering in de kromming optreedt bij x=-1 en bij x=1, zijn dit geen buigpunten. Omdat ze niet tot het domein van de functie behoren.
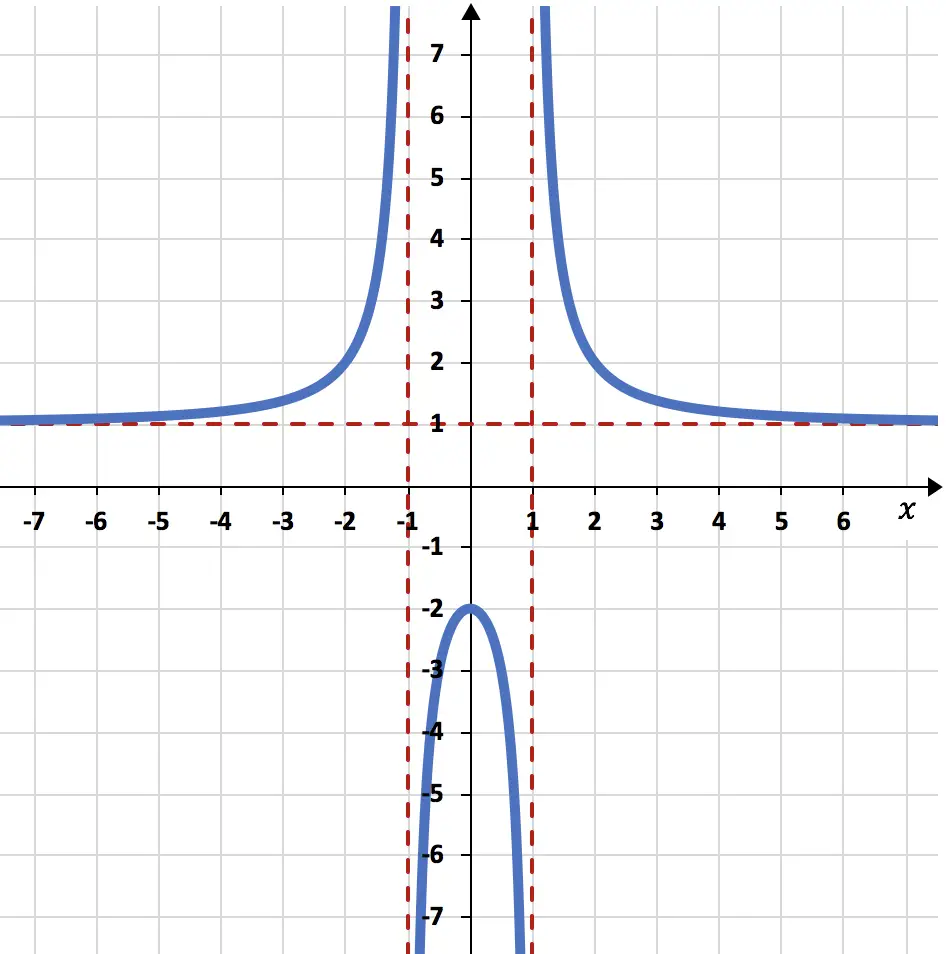
En ten slotte tekenen we de functie in een grafiek met behulp van alle uitgevoerde berekeningen:
Oefening 3
Teken de volgende rationale functie in een grafiek:
![]()
Dit is een rationale functie, dus we moeten de noemer gelijk stellen aan 0 om te zien welke getallen niet tot het domein van de functie behoren:
![]()
![]()
![]()
![]()
![]()
Om het snijpunt met de X-as te vinden, lossen we op
![]()
Omdat de functie op de X-as altijd de waarde 0 heeft:
![]()
![]()
![]()
![]()
![]()
Het snijpunt met de X-as is dus:
![]()
En om het snijpunt met de Y-as te vinden, berekenen we
![]()
Omdat x altijd 0 is op de Y-as:
![]()
Het snijpunt met de Y-as is dus:
![]()
In dit geval valt het snijpunt met de X-as samen met het snijpunt met de Y-as, aangezien de functie door de oorsprong van de coördinaten gaat.
Om te zien of de functie verticale asymptoten heeft, moeten we de limiet van de functie berekenen op punten die niet tot het domein behoren (in dit geval x=-2 en x=+2). En als het resultaat oneindig is, is het een verticale asymptoot. Nog:
![]()
Omdat de limiet van de functie wanneer x -2 nadert, oneindigheid oplevert, is x=-2 een verticale asymptoot.
We berekenen de laterale grenzen van de asymptoot x=-2 door een getal dat er heel dichtbij ligt in de functie te vervangen:
![]()
![]()
Laten we nu eens kijken of x=+2 een verticale asymptoot is:
![]()
Omdat de limiet van de functie wanneer x +2 nadert, oneindigheid oplevert, is x=+2 een verticale asymptoot.
We berekenen de laterale grenzen van de asymptoot x=2 door een getal dat er heel dicht bij ligt in de functie te vervangen:
![]()
![]()
Aan de andere kant zal de horizontale asymptoot van de functie het resultaat zijn van de oneindige limiet van de functie. Nog:
![]()
De oneindige limiet van de functie gaf ons +∞, dus de functie heeft geen horizontale asymptoot.
We berekenen nu de schuine asymptoot. De schuine asymptoten hebben de vorm
![]()
EN
![]()
Het wordt berekend met de volgende formule:
![]()
![]()
![]()
Zodra we de helling van de schuine asymptoot kennen, bepalen we het snijpunt met behulp van de volgende formule:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
Maar we verkrijgen de onbepaaldheid ∞ – ∞. Het is daarom noodzakelijk om de termen terug te brengen tot een gemeenschappelijke noemer. Om dit te doen, vermenigvuldigen en delen we de x door de noemer van de breuk:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
Kort gezegd is de schuine asymptoot:
![]()
![]()
![]()
Om de monotoniciteit van de functie te bestuderen, moeten we eerst de afgeleide berekenen:
![]()
![]()
Nu stellen we de afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
We geven nu op de lijn alle gevonden singuliere punten weer, dat wil zeggen de punten die niet tot het domein behoren (x=-2 en x=+2) en die welke de afgeleide opheffen (x=0, x=- 3,46 en x= +3,46):

En we evalueren het teken van de afgeleide in elk interval, om te weten of de functie toeneemt of afneemt. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de afgeleide op dit punt heeft:
![]()
![]()
![]()
![]()
![]()
![]()
Als de afgeleide positief is, betekent dit dat de functie toeneemt, en als de afgeleide negatief is, betekent dit dat de functie afneemt. Daarom zijn de groei- en dalingsintervallen:
Groei:
![]()
Afname:
![]()
De functie gaat van stijgend naar dalend bij x=-3,46, dus x=-3,46 is een maximum van de functie. En de functie gaat van afnemend naar toenemend bij x=3,46, dus x=3,46 is een minimum van de functie.
We bepalen de Y-coördinaten van de relatieve uiteinden:
![]()
![]()
De relatieve uitersten van de functie zijn daarom:
Maximaal op punt
![]()
Minimaal tot punt
![]()
Om de kromming van de functie te bestuderen, berekenen we de tweede afgeleide van de functie:



![]()
![]()
![]()
![]()
Nu stellen we de tweede afgeleide gelijk aan 0 en lossen we de vergelijking op:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
Er is geen oplossing omdat er geen negatieve wortel is van een reëel getal.
We geven nu op de lijn alle gevonden singuliere punten weer, dat wil zeggen de punten die niet tot het domein behoren (x=-2 en x=+2) en die welke de tweede afgeleide (x=0) opheffen:

En we evalueren het teken van de tweede afgeleide in elk interval, om te weten of de functie concaaf of convex is. We nemen daarom in elk interval een punt (nooit de singuliere punten) en kijken welk teken de tweede afgeleide op dit punt heeft:
![]()
![]()
![]()
![]()

Als de tweede afgeleide positief is, betekent dit dat de functie convex is.
![]()
, en als de tweede afgeleide negatief is, betekent dit dat de functie concaaf is
![]()
. De concaviteits- en convexiteitsintervallen zijn daarom:
Convex
![]()
:
![]()
Concaaf
![]()
:
![]()
Hoewel er echter een verandering in de kromming optreedt bij x=-2 en x=+2, zijn dit geen buigpunten. Omdat x=-2 en x=+2 niet tot het domein van de functie behoren. Aan de andere kant is er bij x=0 een verandering in de kromming (de functie gaat van convex naar concaaf) en dit hoort bij de functie, dus x=0 is een buigpunt.
We vervangen de gevonden buigpunten in de originele functie om de andere coördinaat van het buigpunt te vinden:
![]()
De keerpunten van de functie zijn daarom:
Keerpunten:
![]()
Ten slotte vertegenwoordigen we, op basis van alle informatie die we hebben berekend, de functie:
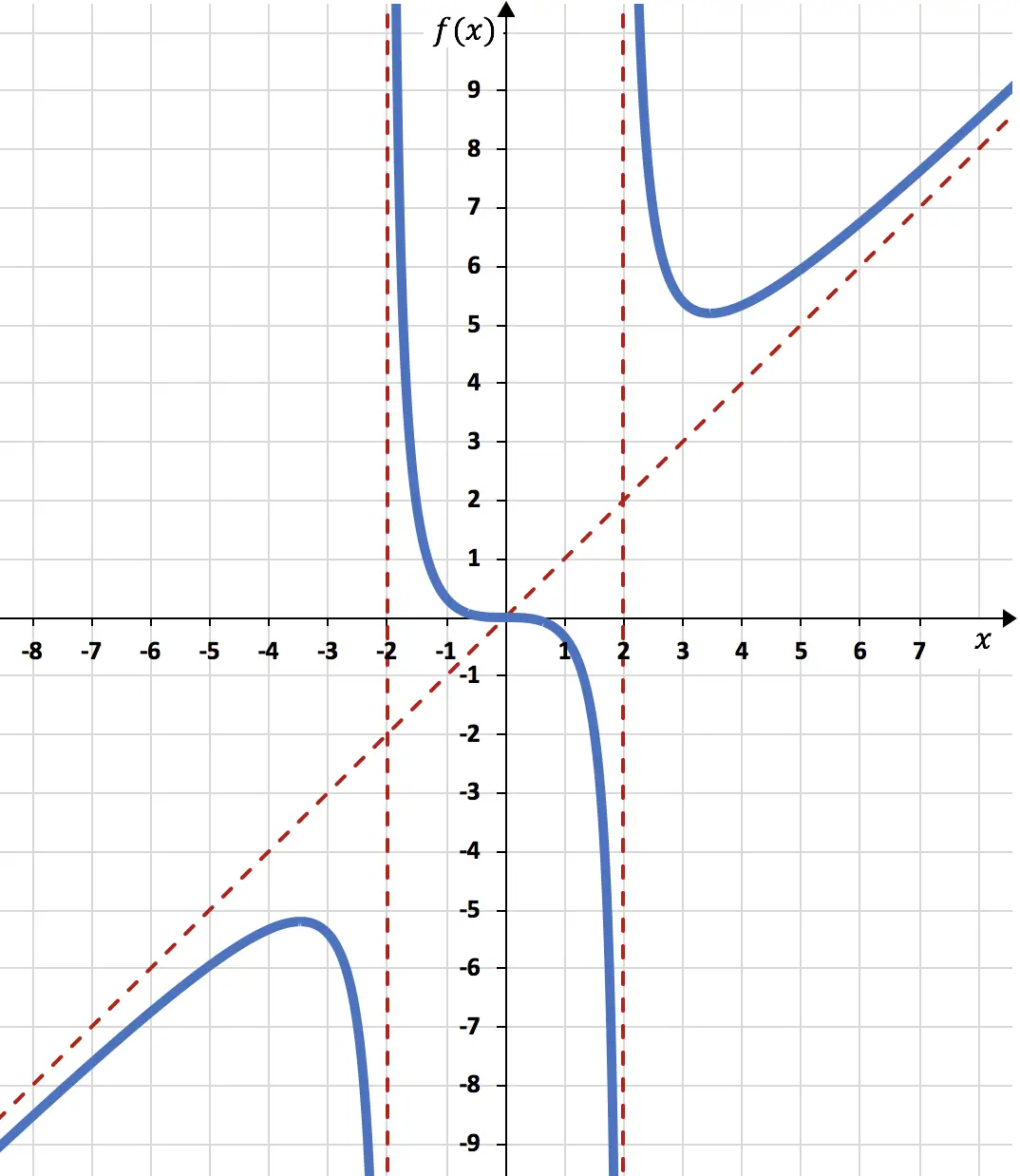
Opmerking: Merk op dat de functie op dit punt de schuine asymptoot kruist
![]()
De schuine asymptoten bepalen vooral het gedrag van de functie wanneer x neigt naar +∞ en -∞. In feite kruist de functie nooit de schuine asymptoot rechts van de grafiek (x →+∞) en links van de grafiek (x →-∞). Het komt echter zeer zelden voor dat de functie de schuine asymptoot in het midden kruist; dit is een heel speciaal geval.