Op deze pagina vindt u uitleg over wat de componenten (of coördinaten) van een vector zijn. Je zult ook kunnen zien hoe ze worden berekend vanuit twee punten en zelfs hoe ze worden ontleed via hun module en hun hoek. Daarnaast vind je voorbeelden en oefeningen die stap voor stap worden opgelost.
Wat zijn de componenten van een vector?
De componenten van een vector zijn de projecties van een vector op de cartesiaanse assen. Daarom is de projectie van de vector op de x-as de X-component van de vector en op dezelfde manier is de projectie van de vector op de y-as de Y-component van de vector.
De componenten van een vector kunnen ook de coördinaten van een vector worden genoemd.
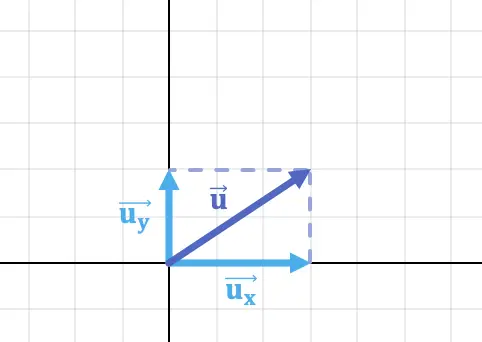
De horizontale component en de verticale component van de vector in de afbeelding hierboven zijn bijvoorbeeld:
![]()
![]()
De vector is dus:
![]()
Daarom kunnen de componenten van een vector ook worden gedefinieerd als de weergave van een vector in een coördinatensysteem. Als het een tweedimensionaal systeem is (in r2), zal de vector uiteraard twee componenten hebben. Als het daarentegen een driedimensionale basis is (in r3), zal de vector uit drie componenten bestaan.
De cartesiaanse componenten van een vector zijn zo belangrijk omdat we daarmee de kenmerken van de vector kunnen kennen, die voornamelijk de richting, de betekenis en de modulus (of grootte) van de vector zijn. Bovendien worden ze gebruikt om vectorbewerkingen uit te voeren.
Hoe de componenten van een vector uit twee punten te berekenen
We hebben zojuist gezien hoe we de coördinaten van een vector grafisch kunnen vinden, maar we kunnen de componenten ook numeriek bepalen.
Om de componenten van een vector numeriek te berekenen, moeten we twee punten kennen: de oorsprong en het einde, of met andere woorden, waar hij begint en waar hij eindigt. Omdat de componenten van een vector de coördinaten zijn die we verkrijgen door het einde minus de oorsprong ervan af te trekken.
![]()
We berekenen bijvoorbeeld de vector waarvan de oorsprong punt A(3,1) is en het einde punt B(5,4):
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Zoals u kunt zien, is het bepalen van de componenten van een vector niet erg moeilijk, maar wel behoorlijk belangrijk. Een van de meest gebruikte soorten vectoren zijn bijvoorbeeld loodrechte (of orthogonale) vectoren; Als je begrijpt wat de coördinaten van een vector zijn, is het heel eenvoudig om loodrechte vectoren te berekenen. Je kunt zien hoe het moet in de uitleg van orthogonale vectoren .
Hoe de componenten van een vector te berekenen op basis van zijn modulus en hoek
Je kunt de componenten van een vector ook vinden aan de hand van de grootte ervan en de hoek die deze maakt met de X-as. Dit proces wordt vectorontleding genoemd.
Zo kunnen de X- en Y-componenten van de vector worden berekend met de trigonometrische verhoudingen van de cosinus en de sinus:

Zoals je in de afbeelding kunt zien, vormen de modulus van een vector en zijn componenten een rechthoekige driehoek, zodat de elementaire formules van de trigonometrie kunnen worden toegepast.
Als u niet meer weet hoe de modulus van een vector wordt berekend, kunt u opzoeken wat de modulus van een vector is . Hier vind je de formule voor de grootte van een vector, evenals voorbeelden, stap-voor-stap opgeloste oefeningen en alle eigenschappen van de grootte van een vector. Dit is een zeer volledige uitleg, zodat u deze perfect zult begrijpen. ✅
In tegenstelling tot de grootte van een vector die altijd positief is, kunnen de componenten ervan negatief zijn omdat de sinus en cosinus negatieve waarden kunnen aannemen.
Als voorbeeld zullen we de vectorontleding uitvoeren van de vector waarvan de module en de hoek met de OX-as zijn:
![]()
De X-component van de vector is gelijk aan de module vermenigvuldigd met de cosinus van de hoek:
![]()
En de Y-component van de vector is gelijk aan het product van de module en de sinus van de hoek:
![]()
De coördinaten van de vector zijn dus:
![]()