Gemengd product van drie vectoren (of drievoudig puntproduct)

Op deze pagina leggen we uit wat het gemengde product van drie vectoren (of triple dot product) is en hoe dit wordt berekend. Je zult ook voorbeelden, oefeningen en opgeloste problemen zien over dit soort operaties tussen vectoren. En daarnaast vindt u de eigenschappen en toepassingen van het gemengde product.

Wat is het gemengde product van drie vectoren?

Het gemengde product van drie vectoren, ook wel het drievoudige puntproduct genoemd, is een opeenvolgende vermenigvuldiging tussen drie vectoren waarbij twee verschillende soorten bewerkingen betrokken zijn: het puntproduct en het vectorproduct . De combinatie van de twee vectorbewerkingen geeft dus een scalair (een reëel getal).

Concreet bestaat het gemengde product uit het berekenen van het vectorproduct van twee vectoren en het vervolgens vectorisch vermenigvuldigen van het resultaat dat wordt verkregen met een derde vector. Zo geschreven lijkt het misschien erg ingewikkeld, maar in werkelijkheid is het niet zo veel, kijk eens naar de triple dot productformule:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})$

Zoals je in de formule kunt zien, wordt het gemengde product van drie vectoren aangegeven door twee vierkante haken.

Hoe bereken je het gemengde product van drie vectoren?

De productformule met drie punten is degene die we zojuist in de vorige sectie hebben gezien, maar wordt over het algemeen niet gebruikt om het gemengde product van drie vectoren te bepalen, omdat er een andere, eenvoudigere en snellere manier is:

Laat elke 3 vectoren zijn:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)$

Om het gemengde product tussen drie vectoren te berekenen, lost u eenvoudigweg de 3×3-determinant op die wordt gevormd door de componenten van de vectoren:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}$

U kunt dus een voorbeeld zien van hoe dit wordt berekend . We vinden het gemengde product van de volgende drie vectoren:

$\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)$

Om het gemengde product te bepalen, construeren we een determinant van orde 3 door de vectoren in rijen van de matrix te plaatsen:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

En nu moeten we alleen de determinant van de matrix oplossen, hiervoor kun je elke methode gebruiken. In dit geval passen we de regel van Sarrus toe (maar dit kan ook door toevoegingen of cofactoren):

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}$

Om aan te tonen dat de twee procedures gelijkwaardig zijn, zullen we het gemengde product van dezelfde vectoren berekenen aan de hand van hun definitie:

$\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}$

Wij raden aan om het gemengde product te berekenen via de determinant van de vectoren, omdat dit sneller is en er minder kans is op fouten. Maar zoals u kunt zien, is het resultaat hetzelfde, ongeacht welke methode u gebruikt, dus gebruik de methode die u verkiest. 👍

Geometrische interpretatie van het gemengde product

Als je eenmaal weet hoe je het gemengde product van drie vectoren kunt vinden, vraag je je misschien af… en waar is het gemengde product voor? Welnu, in de wiskunde heeft het twee belangrijke toepassingen: het berekenen van het volume van een parallellepipedum en het volume van een tetraëder.

Het volume van een parallellepipedum is gelijk aan de absolute waarde van het gemengde product van de vectoren die de 3 dimensies van het geometrische veld markeren.

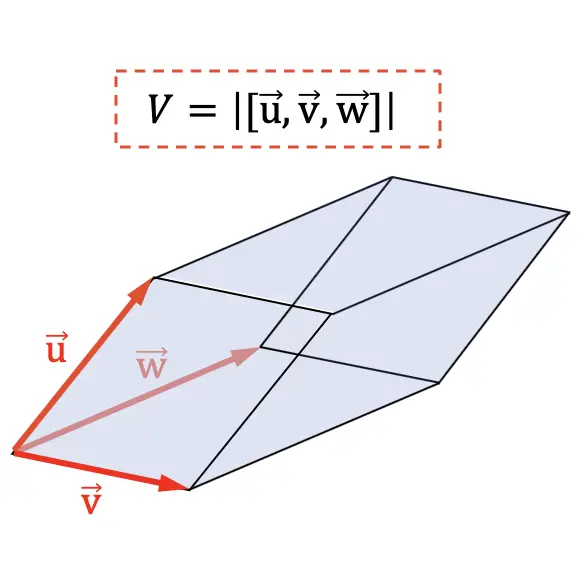
voorbeeld van een gemengd product van drie vectoren of een drievoudig scalair product

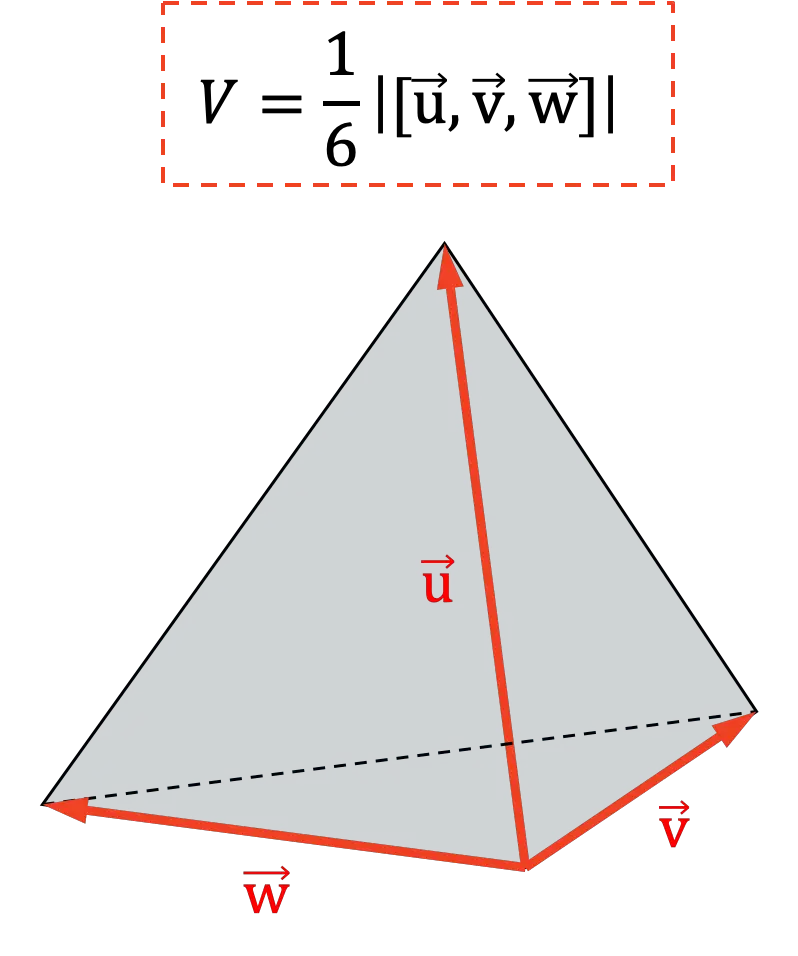
Een andere toepassing van het gemengde product is het bepalen van het volume van een tetraëder . Omdat geometrisch het zesde deel van de absolute waarde van het gemengde product het volume van een tetraëder vertegenwoordigt:

Eigenschappen van het gemengde product of triple dot product

Het gemengde product, of drievoudig scalair product, heeft de volgende kenmerken:

Over het algemeen impliceert een verandering in de volgorde van gemengde productvectoren ook een tekenverandering. Daarom is de volgorde van de gemengde productvectoren belangrijk.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]$

Als we de volgorde echter cyclisch veranderen, verandert het teken niet:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]$

In een driedimensionale ruimte (in R3) is het gemengde product van drie lineair afhankelijke of coplanaire vectoren (die tot hetzelfde vlak behoren) gelijk aan 0.

Problemen met gemengde producten opgelost

Oefening 1

Gegeven 3 vectoren:

$\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)$

Bereken het gemengde product van de drie vectoren:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

zie oplossing

Om het gemengde product ervan te vinden, moeten we de determinant oplossen die is samengesteld uit de coördinaten van de vectoren:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}$

Oefening 2

Gegeven 3 vectoren:

$\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)$

Bepaal het gemengde product tussen de drie vectoren:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

zie oplossing

Om het gemengde product ervan te vinden, moeten we de determinant oplossen die de cartesiaanse coördinaten van de vectoren in lijnvorm heeft:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}$

Oefening 3

Bereken het volume van het parallellepipedum waarvan de 3 zijden de volgende vectoren zijn:

$\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)$

zie oplossing

Het volume van een parallellepipedum is gelijk aan de absolute waarde van het gemengde product van 3 van de vectoren die het als randen heeft. Daarom berekenen we eerst het drievoudige kruisproduct van de vectoren:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}$

Zodat het volume van het parallellepipedum de absolute waarde is van het resultaat van het gemengde product:

$V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}$

Oefening 4

Bereken het volume van de tetraëder waarvan de hoekpunten de volgende punten zijn:

$A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)$

zie oplossing

Eerst berekenen we de vectoren die de randen van de tetraëder vertegenwoordigen:

$\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)$

$\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)$

$\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)$

Het volume van een tetraëder is gelijk aan een zesde van de absolute waarde van het gemengde product van 3 van de vectoren die het voor de randen heeft. Daarom berekenen we eerst het gemengde product van de gevonden vectoren:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}$

Het volume van de tetraëder zal dus een zesde zijn van de absolute waarde van het gemengde product:

$V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}$

Wat is het gemengde product van drie vectoren?

Hoe bereken je het gemengde product van drie vectoren?

Geometrische interpretatie van het gemengde product

Eigenschappen van het gemengde product of triple dot product

Problemen met gemengde producten opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren