Soortgelijke of soortgelijke matrices

Op deze pagina vind je de uitleg van soortgelijke matrices, ook wel soortgelijke matrices genoemd. Bovendien laten we u een duidelijk voorbeeld zien van twee vergelijkbare matrices en alle eigenschappen van dit type matrices, zodat u geen twijfels heeft. Ten slotte zul je zelfs kunnen zien hoe ze zich verhouden tot congruente matrices.

Wat zijn vergelijkbare (of vergelijkbare) matrices?

De definitie van soortgelijke matrices is als volgt:

twee matrixen

$A$

$B$

zijn vergelijkbaar (of vergelijkbaar) als er een matrix bestaat

$P$

waarmee aan de volgende voorwaarde wordt voldaan:

$P^{-1}AP = B$

Of gelijkwaardig:

$AP = PB$

In feite de matrix

$P$

fungeert als basisveranderingsmatrix. Wat deze vergelijking betekent, is dus dat de matrix

$A$

kan worden uitgedrukt in een andere grondtal (

$P$

), waaruit de matrix ontstaat

$B$

Deze term kan ook een gelijkenistransformatie worden genoemd, omdat we feitelijk de matrix transformeren

$A$

in de matrix

$B$

Uiteraard de matrix

$P$

het moet een reguliere of niet-gedegenereerde matrix zijn (niet-nul determinant).

Aan de andere kant kunnen we aangeven dat twee matrices vergelijkbaar zijn met de volgende uitdrukking:

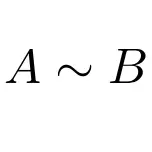
uitleg van soortgelijke of soortgelijke matrices

Deze klasse matrices is belangrijker dan het lijkt voor lineaire algebra. Ze worden voornamelijk gebruikt voor diagonaliseerbare matrices, omdat de procedure voor het diagonaliseren van elke matrix gebaseerd is op het concept van matrixovereenkomst.

In feite omvat het proces van het diagonaliseren van een matrix het berekenen van een soortgelijke matrix die tegelijkertijd een diagonale matrix is. U kunt zien hoe u dit doet bij het diagonaliseren van een matrix .

Voorbeeld van vergelijkbare of vergelijkbare matrices

Vervolgens zullen we een voorbeeld zien van vergelijkbare matrices met dimensie 2×2 om het concept te assimileren.

De vierkante matrices A en B zijn vergelijkbaar met elkaar via de inverteerbare matrix P:

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

Om aan te tonen dat dit onderling vergelijkbare matrices zijn, moeten we eerst de inverse matrix van P berekenen:

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

En nu controleren we of ze vergelijkbaar zijn door het matrixproduct uit te voeren dat de gelijkenis van twee matrices definieert:

$\displaystyle P^{-1}AP = B \quad ?$

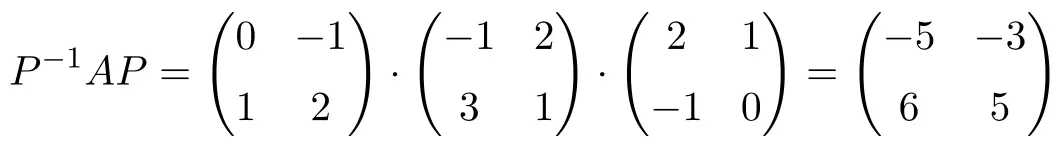
voorbeelden van vergelijkbare of vergelijkbare 2x2-matrices

$\displaystyle P^{-1}AP = B$

✅

Ja, aan de gelijkenisrelatie is voldaan, dus het zijn vergelijkbare matrices.

Soortgelijke matrixeigenschappen

Twee vergelijkbare matrices A en B hebben de volgende kenmerken:

Zelfde rang.

$rg(A)=rg(B)$

De determinanten van de twee matrices zijn hetzelfde.

$det(A)=det(B)$

Zelfde tracering.

$tr(A)=tr(B)$

Dezelfde eigenwaarden (of eigenwaarden). De eigenvectoren (of eigenvectoren) zijn echter meestal verschillend.

Dezelfde karakteristieke polynoom en minimumpolynoom.

Het transponeren van een matrix is vergelijkbaar met de originele matrix.

Matrix B kan worden gevonden door elementaire bewerkingen toe te passen op de rijen van matrix A, en omgekeerd.

Het is duidelijk dat de gelijkenis wordt weerspiegeld. Dat wil zeggen: als A gelijkaardig is aan B, dan is B ook gelijkaardig aan A.

Bovendien is de gelijkenis van matrices ook symmetrisch. Met andere woorden, als met de matrix P de matrix kan worden verkregen die vergelijkbaar is met A (B), kan de matrix die vergelijkbaar is met B (A) ook worden verkregen met dezelfde matrix P:

$B=P^{-1}AP$

$A=PBP^{-1}$

Bovendien is gelijkenis transitief. Dus als matrix A vergelijkbaar is met matrix B en matrix B vergelijkbaar is met matrix C, is matrix A ook vergelijkbaar met matrix C.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

Ten slotte is elke dobbelsteen vergelijkbaar met een zaagtandmatrijs. En uit deze eigenschap kunnen we het volgende gevolgtrekking afleiden: elke vierkante matrix is vergelijkbaar met een driehoekige matrix.

congruente matrices

Aan de andere kant is er ook nog een andere zeer vergelijkbare relatie tussen matrices, maar in plaats van met de inverse matrix, is het met de getransponeerde matrix. Dit heet congruentie .

Twee matrices A en B zijn congruent als er een inverteerbare matrix P bestaat waarmee aan de volgende gelijkheid wordt voldaan:

$P^tAP = B$

Zoals je kunt zien, is dit analoog aan vergelijkbare matrices, maar dan met de matrix getransponeerd.

Soortgelijke of vergelijkbare matrices

Wat zijn vergelijkbare (of vergelijkbare) matrices?

Voorbeeld van vergelijkbare of vergelijkbare matrices

Soortgelijke matrixeigenschappen

congruente matrices

Laat een reactie achter Reactie annuleren